1.SVD
SVD: Singular Value Decomposition,奇异值分解
SVD算法不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算法的基石。
假设我们现在有一个矩阵M(m×n),如果其存在一个分解:M = UDV^T^
其中,U(m×m,酉矩阵,即U^T^=U^-1^);
D(m×n,半正定矩阵);
V^T^(n×n,酉矩阵,V的共轭转置矩阵);
==这样的分解称为M的奇异值分解。==
**D对角线上的元素称为奇异值;
U称为左奇异矩阵;
V^T^称为右奇异矩阵。**
2.SVD奇异值分解与特征值分解的关系
特征值分解与SVD奇异值分解的目的都是提取一个矩阵最重要的特征。
==然而,特征值分解只适用于方阵,而SVD奇异值分解适用于任意的矩阵,不一定是方阵。==
M^T^M = (UDV^T^)^T^UDV^T^=V(D^T^D)V^T^
MM^T^ = UDV^T^(UDV^T^)^T^=U(DD^T^)U^T^
这里,M^T^M和MM^T^是方阵;
U^T^U和V^T^为单位矩阵,
V^T^为M^T^M的特征向量,
U为MM^T^的特征向量。
==M^T^M 和MM^T^的特征值为M的奇异值的平方==
3.SVD奇异值分解的作用核意义
==奇异值分解最大的作用就是数据的降维==
m×n的矩阵M,进行奇异值分解:
M(m×n) = U(m×m)D(m×n)V^T^(n×n)
取其前r个非零奇异值,可以还原原来的矩阵,即前个非零奇异值对应的奇异向量代表了矩阵的主要特征。
可以表示为:
M(m×n)约等于 U(m×r)D(r×r)V^T^(r×n)
4.matlab实现SVD
%% 测试奇异值分解过程
load A.mat;%该文件是做好的一个手写体的图片(28*28 uint8类型)
% for i = 1:28
% j = 28*(i-1)+1;
% B(i,:) = A(1,j:j+27);
% end
B = zeros(28,28);%将行向量重新转换成原始的图片
% 方法一:uint8转double类型
for i = 1:28
for j = 1:28
B(i,j) = A(i,j);
end
end
% % 方法二:uint8转double
% B = im2double(A);
%进行奇异值分解
[U S V] = svd(B);
% U:左奇异矩阵
% S:对角矩阵,对角线上的元素是奇异值,从大到小排列
% V:右奇异矩阵
%选取前面14个非零奇异值
for i = 1:14
for j = 1:14
S_1(i,j) = S(i,j);
end
end
%左奇异矩阵
for i = 1:28
for j = 1:14
U_1(i,j) = U(i,j);
end
end
%右奇异矩阵
for i = 1:28
for j = 1:14
V_1(i,j) = V(i,j);
end
end
B_1 = U_1*S_1*V_1';
%同时输出两个图片
subplot(121);imshow(B); % B是没降维之前
subplot(122);imshow(B_1); % B_是降维后之的这里有一个疑问?
B是28 28,B_也是28 28的啊?不是说好的降维呢?
我是这么理解的:
实际上,取前r=14个奇异值,再重构图片,这就是一个降维过程啊,
以前一张图片是m×n,现在把它分解成后,取奇异值前r个,
则,左奇异矩阵为:m×r
奇异值矩阵:r×r
右奇异矩阵:r×n
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵,在这儿,r越接近于n,则相乘的结果越接近于A。而这三个矩阵的面积之和(在存储观点来说,矩阵面积越小,存储量就越小)要远远小于原始的矩阵A,我们如果想要压缩空间来表示原矩阵A,我们存下这里的三个矩阵。
==[从28维降到了14维]==
取的r值越大,重构的图片和原始图片越像。(当然是再矩阵行列数范围内)
run result: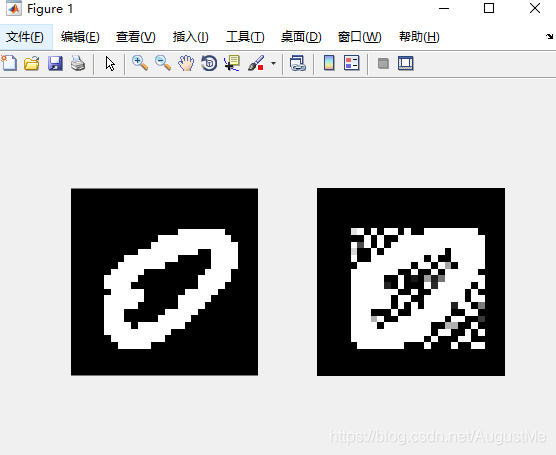
原始的矩阵B: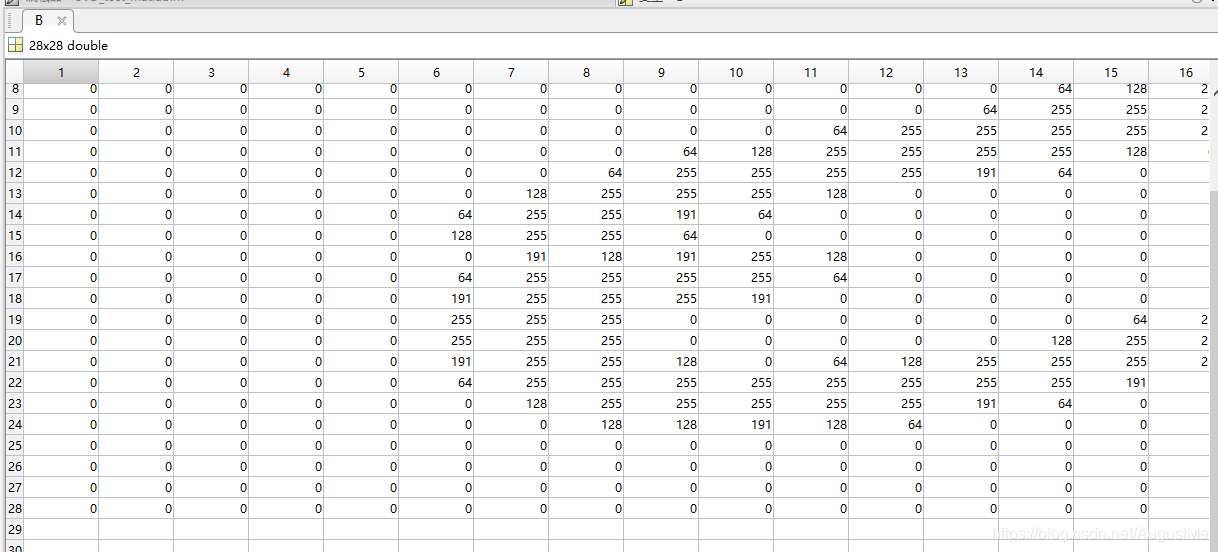
分解后的U: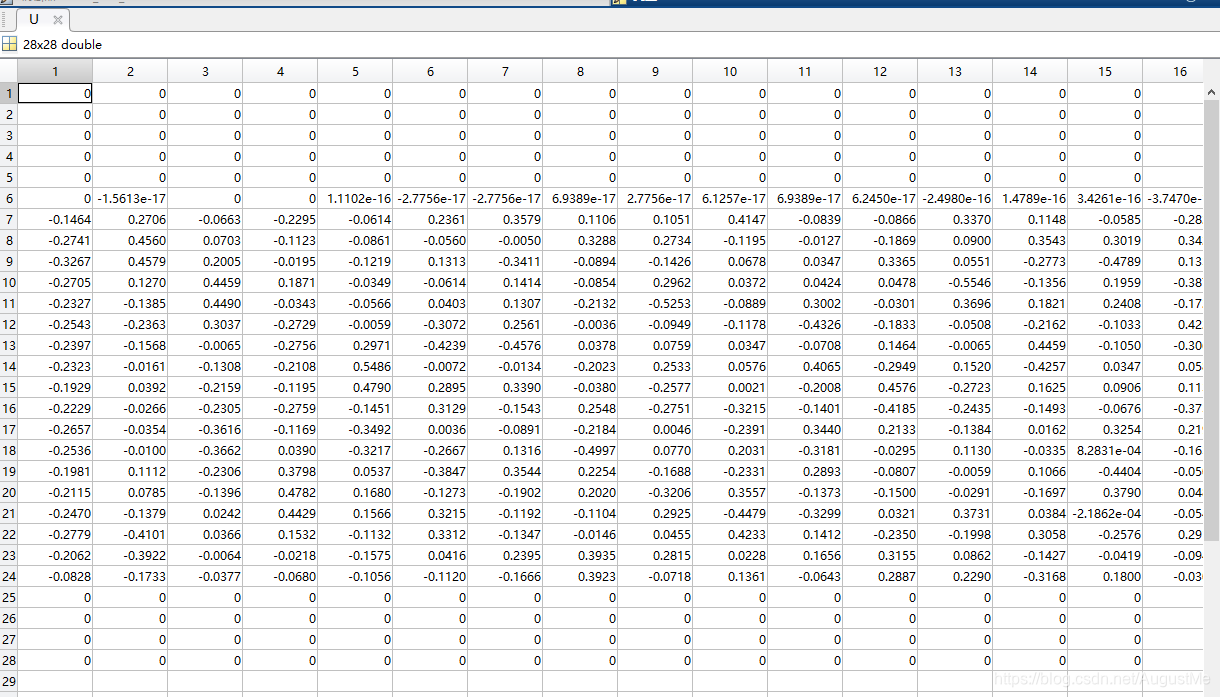
分解后的S: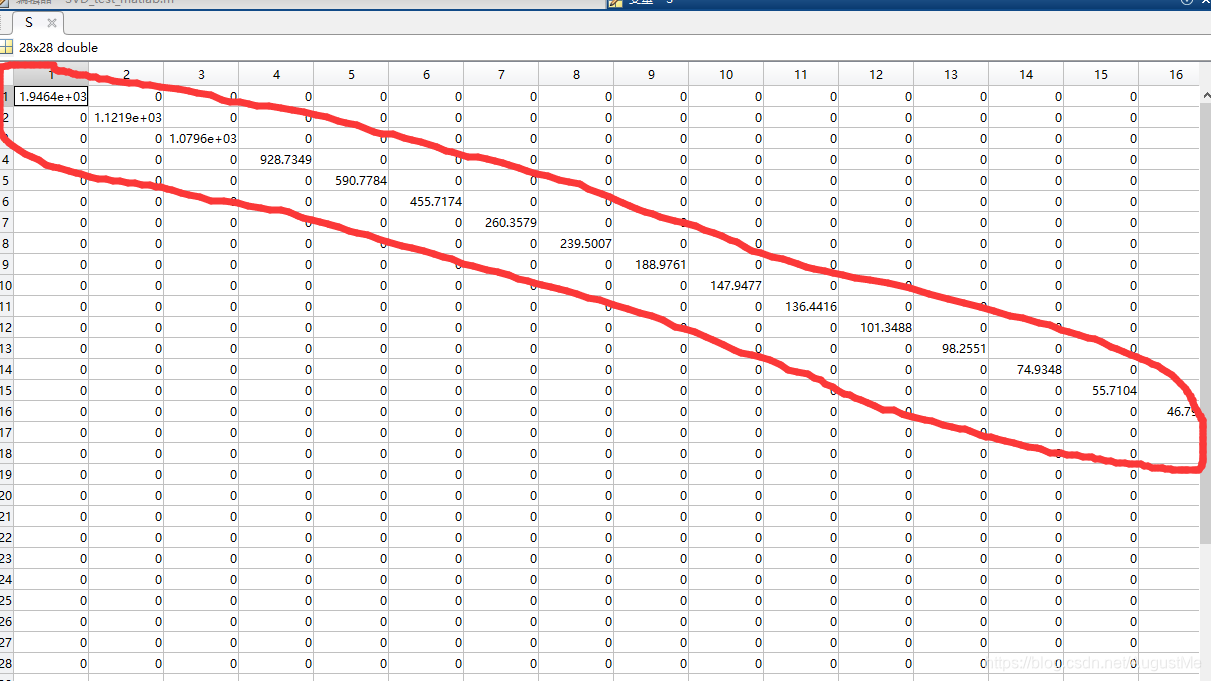
分解后的V: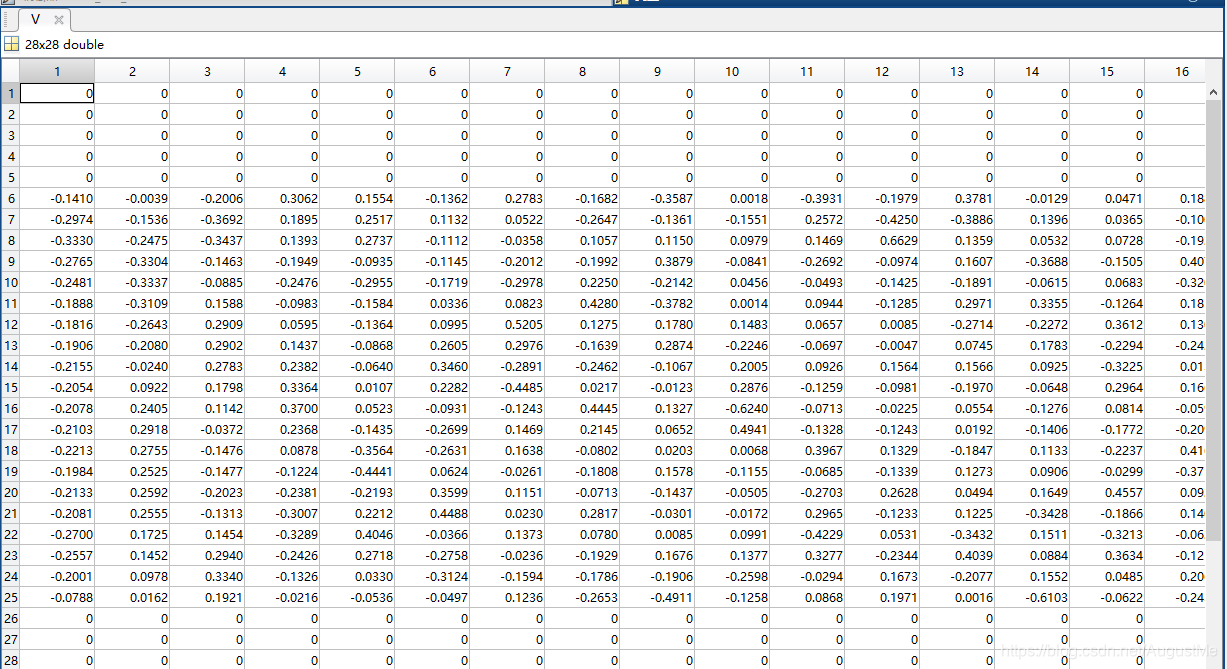
5.python实现SVD
python中的numpy提供了SVD分解算法
函数调用:
np.linalg.svd(a,full_matrices=1,compute_uv=1)
# a:一个m×n矩阵
# full_matrices:取值为0或者1,默认取1,这时u大小为m×m,v的大小为n×n;否则,u的大小为m×k,v的大小为k×n,
# k = min(m,n)
# compute_uv:取值为0或者1,默认取1,表示计算u,s,v;取0表示只计算s
from scipy.io import loadmat
from numpy import linalg as la
from skimage import io # 用于显示图片
import numpy as np
load_data = loadmat('A_0.mat') # 为0手写体
A = load_data['A'] # 获取数据集
A = A[:,0:26]
# 原始图片
io.imshow(A)
#data = np.double(data) # python中svd可直接对uint8进行计算
U,Sigma,VT = la.svd(A)
# Sigma:本身应该是28*26的矩阵,但是只返回一列奇异值不为0组成的向量,为了节省空间
# U:28*28
# V: 26*26
S = np.zeros((28,26))
S[:26,:26] = np.diag(Sigma)
A_recon = np.dot(np.dot(U, S), VT) # 恢复原始维度
io.imshow(A_recon)run result: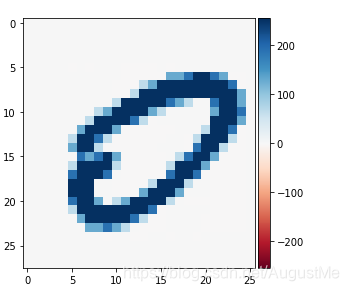
总结:我一直在想降维,是高维到低维,比如2826的矩阵,降到2814的矩阵,这样直观产生数据才对啊,我看网上也有和我同样的疑问,这个SVD分解的过程,到取前r个奇异值,(得到简化的U_1,S_1,V_1,这就是降维啊,哈哈哈)进行数据还原,这个才是SVD的精髓所在。
参考和引用:
https://www.zhihu.com/question/34143886 (SVD 降维体现在什么地方?
感觉即使把分解的三个矩阵变小,可乘回去整个矩阵并没有小。)
https://www.jianshu.com/p/9846fc1c4cac
https://blog.csdn.net/google19890102/article/details/27109235
https://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
https://blog.csdn.net/mingyuli/article/details/81092795
仅用来个人学习和分享,如有错误,请指正。
如若侵权,留言立删。
