Boosting算法是一种把若干个分类器整合为一个分类器的方法,也就是一种集成分类方法(Ensemble Method)。
计量经济学的视角
可以从计量经济学的角度理解提升方法(Boosting)的内容。
这里的目标是要解决:
损失函数ℓ,以及预测器集合M。这是一个优化问题。这里的优化是在函数空间中进行的,是一个简单的优化问题。从数值的角度来看,优化是用梯度下降来解决的(这就是为什么这种技术也被称为梯度提升)。
同样,最佳值不是某个实值x⋆,而是某个函数m⋆。因此,在这里我们会有类似m
其中右边的式子也可以写成
从后者可以清楚地看到f是我们在剩余残差上拟合的模型。
我们可以这样改写:定义
目标是拟合一个模型,使 ri,k=h⋆(xi),当我们有了这个最优函数。设 mk(x)=mk-1(x)+γkh⋆(x)。
这里有两个重要点。
首先,我们拟合一个模型,通过一些协变量 x来解释 y。然后考虑残差 ε,并以相同的协变量 x来解释它们。如果你尝试用线性回归,你会在第1步结束时完成,因为残差 ε与协变量 x是正交的:我们没有办法从它们那里学习。在这里它是有效的,因为我们考虑的是简单的非线性模型。而实际上,可以使用的东西是添加一个收缩参数。不要考虑 ε=y-m(x),而是 ε=y-γm(x) 。弱学习的概念在这里是极其重要的。我们收缩得越多,花的时间就越长。不断从错误中学习是件好事。但从启发式的角度来看,当我们开始过度拟合时,我们应该停止。而这可以通过对初始数据集进行分割训练验证或使用交叉验证来观察。
样条曲线
我们尝试用样条曲线来学习。因为标准的样条曲线有固定的结点,
在这里,我们将(以某种方式)优化结点位置。为了说明问题,这里使用的是高斯回归,而不是分类。考虑以下数据集(只有一个协变量):
对于结点的最佳选择,我们可以使用
lsgen(x, y, degree = 1, numknot = 2)
在5%的收缩参数下,代码简单如下
v=.05 fit=lm(y~bs(x,degree=1,knots=optknot)) yp=predict(fit,newdata=df) yr= y - v*yp YP=v*yp for(t in 1:200){ fit=lm(yr~bs(x,degree=1,knots= optknot) ) plot( x, y,ylab="",xlab="") lines( x,y,type="l" )
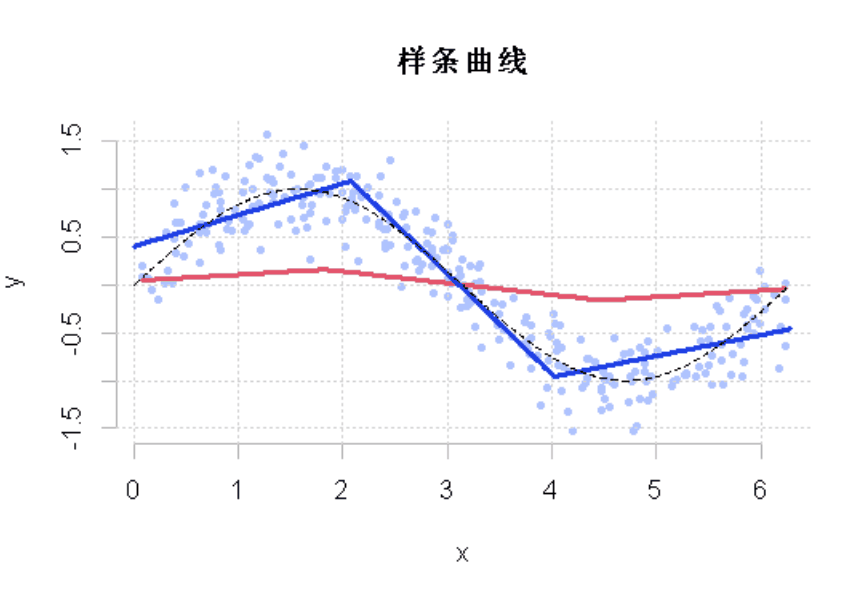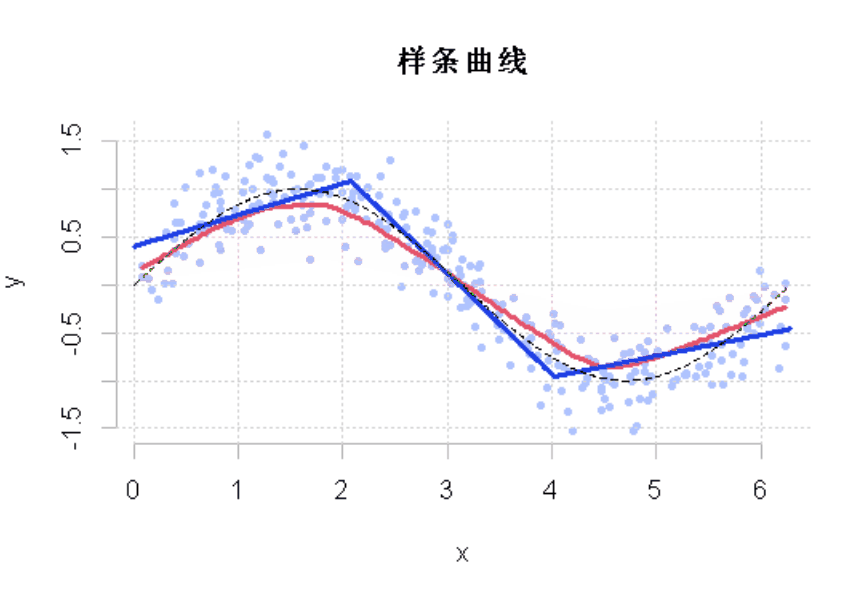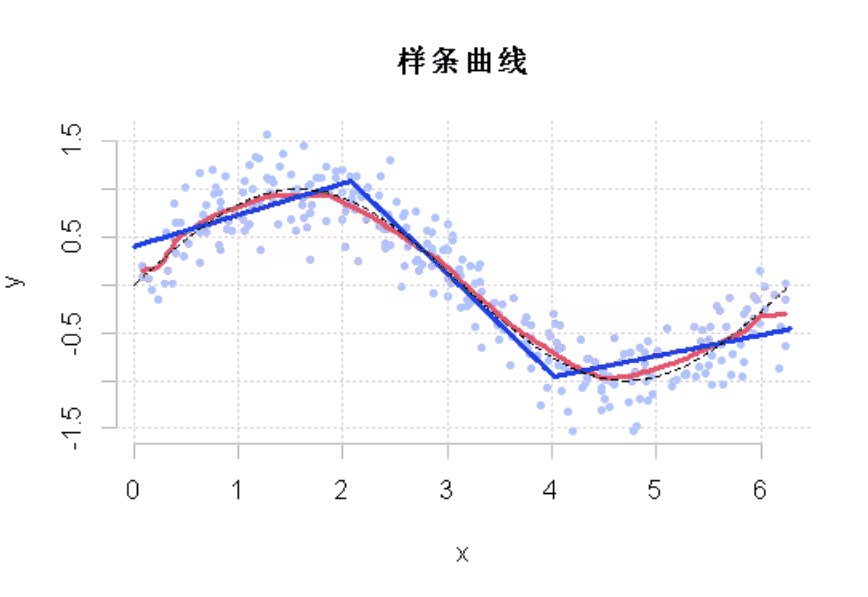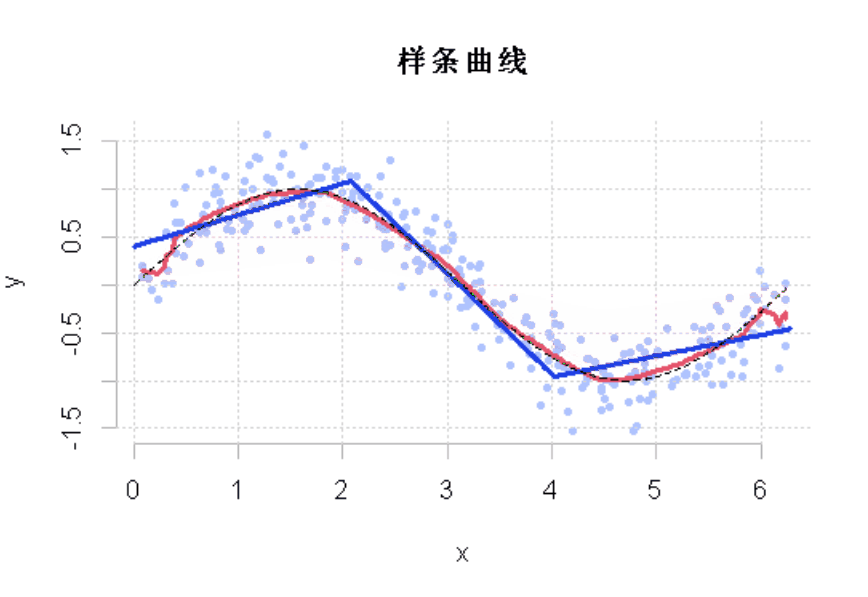
为了直观地看到100次迭代的结果,使用动态可视化
viz(100)
图1
很明显,我们看到,在这里从数据中学习。
决策回归树
我们尝试一下别的模型。如果我们在每一步都考虑决策树,而不是线性逐步回归(这是用线性样条考虑的)。
v=.1 rpart(y~x,data=df) yp=predict(fit) yr= y - yp YP=v*yp for(t in 1:100){ predict(fit,newdata=df)
同样,为了将学习过程动态可视化,使用
plot( x, y,ylab="",xlab="") lines( x,y,type="s" fit=rpart(y~x,data=df)
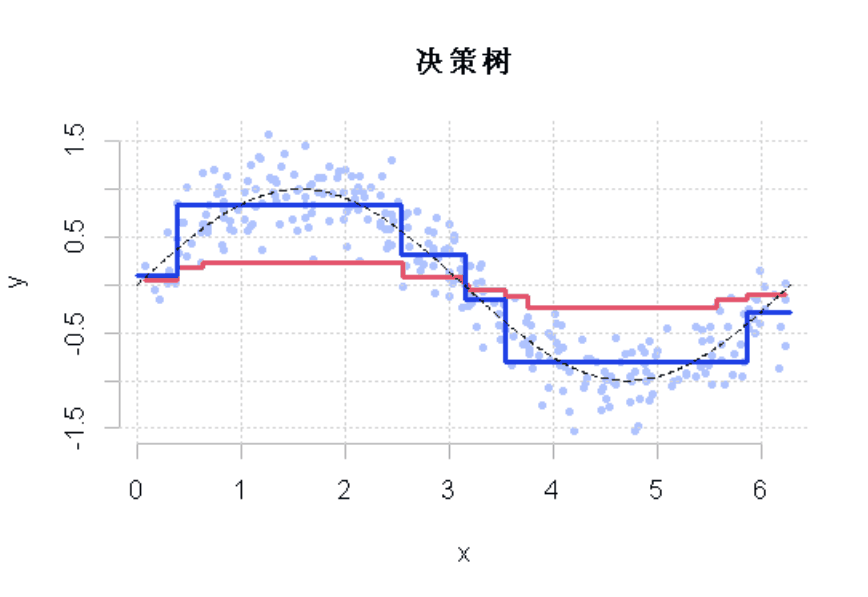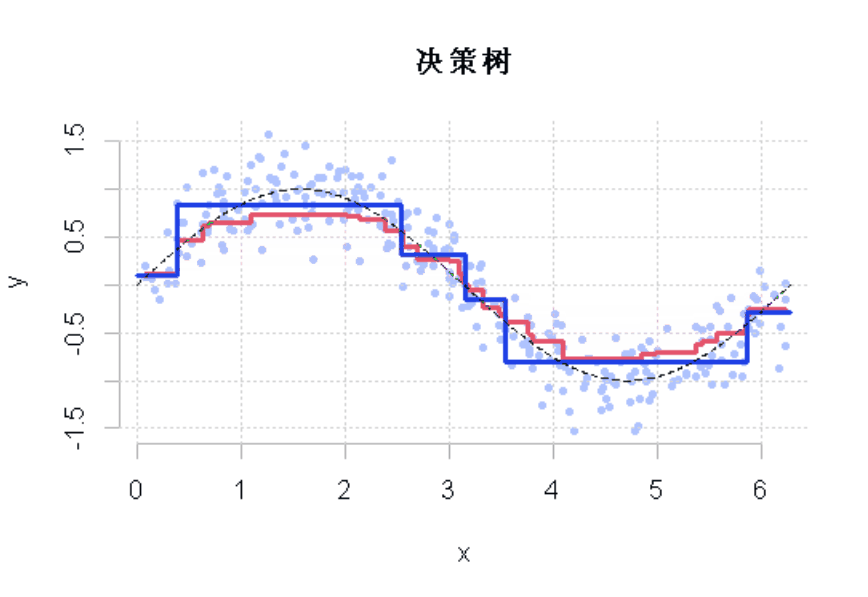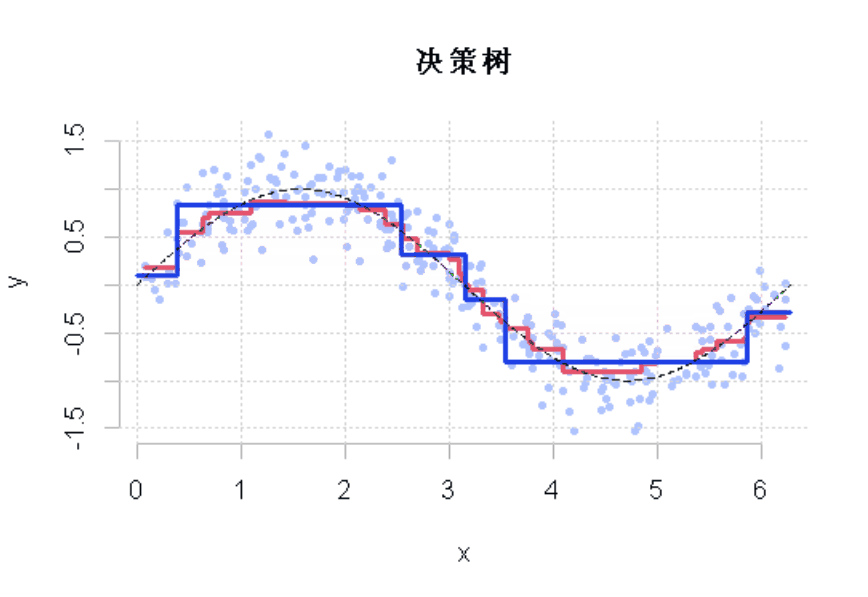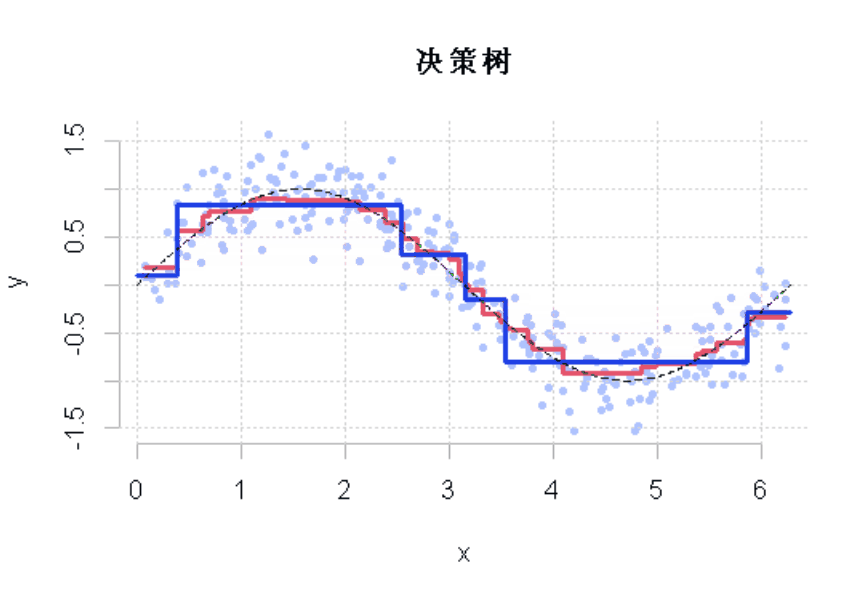
图2
这一次,通过这些树我们不仅有一个好的模型,而且与我们使用单一的回归树所能得到的模型不同。
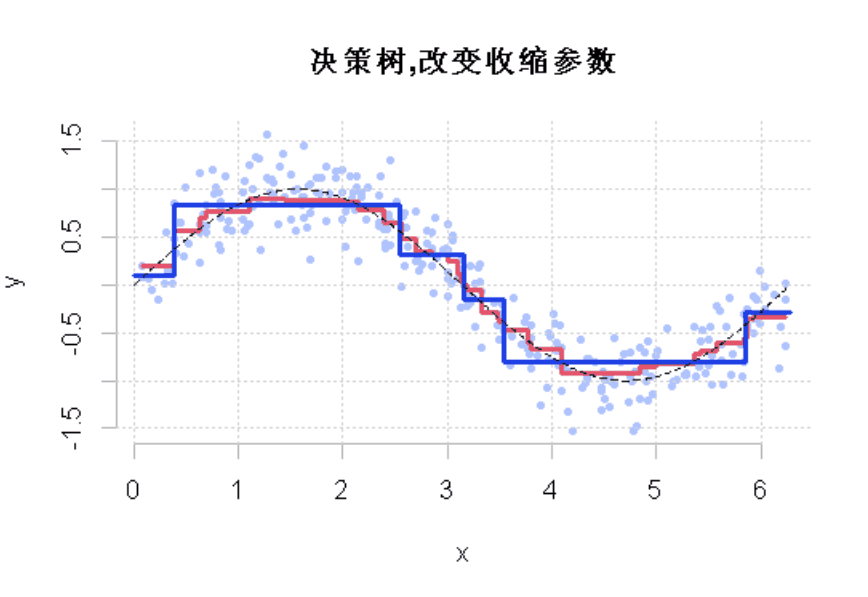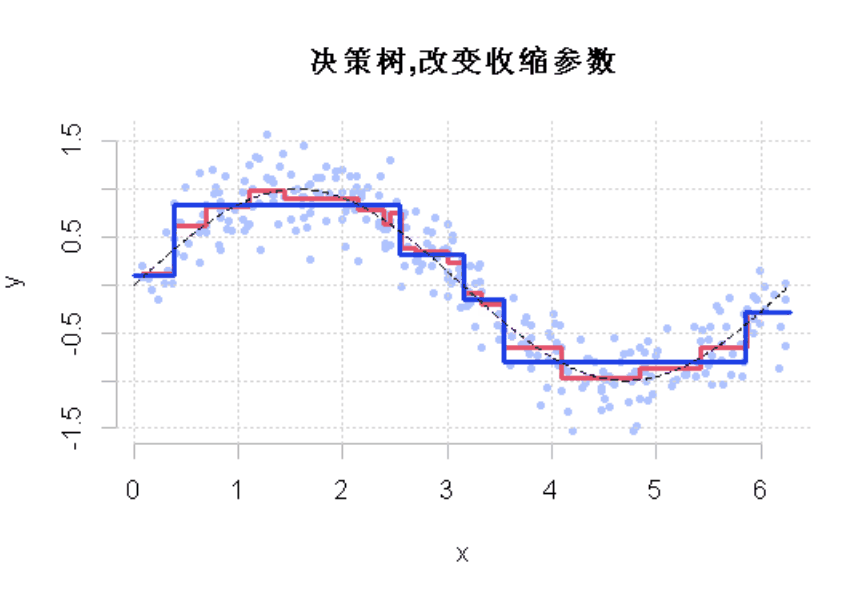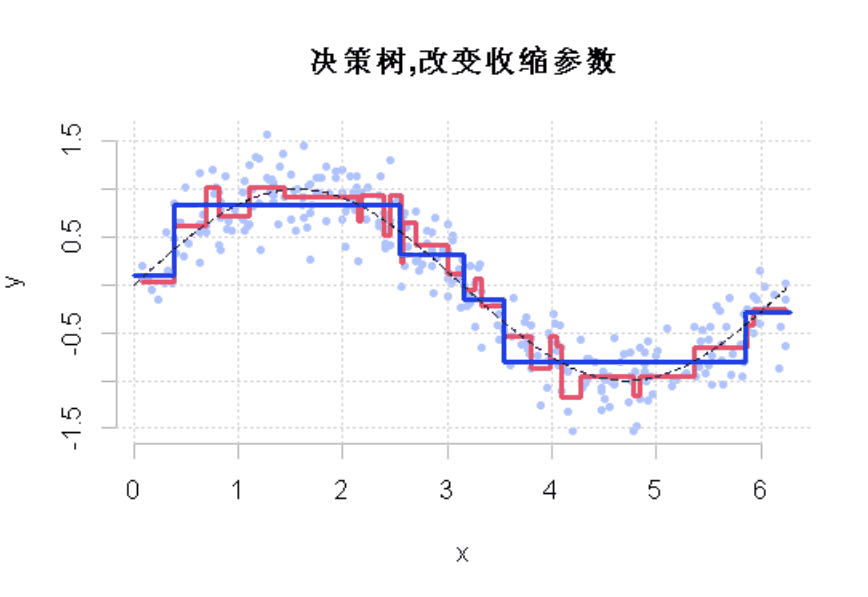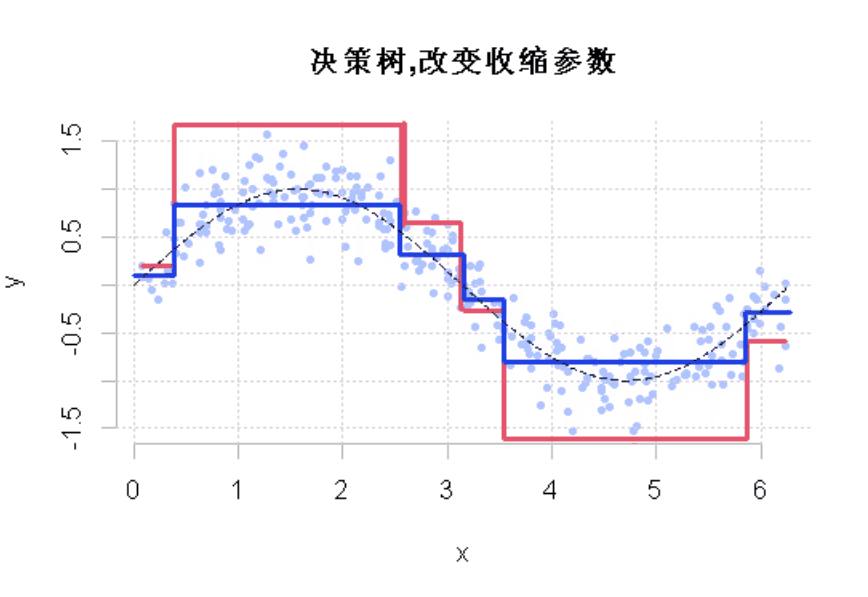
如果我们改变收缩参数呢?
为了直观地看到收缩参数改变的结果,使用动态可视化
viz=function(v=0.05) f$yr=df$y -v*yp YP=v*yp for(t in 1:100){ yp=predict(fit,newdata=df) yr= yr - v*yp lines(df$x,y,type="s"
图3
显然,这个收缩参数有影响。它必须很小才能得到一个好的模型。这就是使用弱学习来获得好的预测的想法。
分类和Adaboost
现在我们了解了bootsting的工作原理,并把它用于分类。这将更加复杂,因为残差在分类中通常信息量不大,而且它很难缩减。因此,让我们尝试一些稍微不同的方法,来介绍adaboost算法,AdaBoost是最著名的Boosting族算法。
在我们最初的讨论中,目标是最小化一个凸的损失函数。在这里,如果我们把类表示为{-1,+1},我们考虑的损失函数是 (与逻辑模型相关的损失函数是 。
我们在这里所做的与梯度下降(或牛顿算法)有关。之前,我们是从误差中学习的。在每个迭代中,计算残差,并对这些残差拟合一个(弱)模型。这个弱模型的贡献被用于梯度下降优化过程。
这里的情况会有所不同,因为更难使用残差,空残差在分类中从不存在。所以我们将增加权重。最初,所有的观察值都有相同的权重。但是,迭代之后,我们将增加预测错误的个体的权重,减少预测正确的个体的权重。
我们从ω0=1n开始,然后在每一步拟合一个模型(分类树),权重为ωk(我们没有讨论树的算法中的权重,但实际上在公式中是很直接的)。让hωk表示该模型(即每个叶子里的概率)。然后考虑分类器 ,它返回一个在{-1,+1}的值。然后设
Ik是被错误分类的个体集合。
然后设置
并在最后更新模型时使用
以及权重
除以总和,以确保总和是1。如前所述,我们可以包括一些收缩参数。为了直观地看到这个过程的收敛性,我们将在我们的数据集上绘制总误差。
for(i in 1:n_iter)rfit = rpart(y~., x, w, method="class") g = -1 + 2*(predict(rfit,x)\[,2\]>.5) e = sum(w*(y*>0)) error\[i\] = mean(1\*f\*y<0) plot(seq(1,n_iter),error
图4
在这里,我们面临一个机器学习中的经典问题:我们有一个完美的模型,误差为零。用多项式拟合:有10个观察值,9度的多项式,拟合很好。将我们的数据集一分为二,一个训练数据集,一个验证数据集。
train\_car = car\[id\_train,\] test\_car= car\[-id\_train,\]
我们在第一个模型上构建模型,并在第二个模型上检查
for(i in 1:n_iter){ rfit = rpart(y\_train~., x\_train, w_train, method="class") train\_error\[i\] = mean(1\*f\_train\*y_train<0) test\_error\[i\] = mean(1\*f\_test\*y_test<0)} plot(seq(1,n\_iter),test\_error)
图5
在这里,和以前一样,经过80次迭代,我们在训练数据集上有一个不错的模型,但在验证数据集上表现得很差。在20次迭代后,效果比较好。
R函数:梯度提升(_GBM_)算法
也可以使用R函数。
gbm(y~ .,n.trees = 200,shrinkage = .01,cv.folds = 5
这里考虑的是交叉验证,而不是训练验证,以及用得是森林而不是单棵树,当然,输出要好得多(这里收缩参数是一个非常小的参数,而且学习非常慢)。
图6