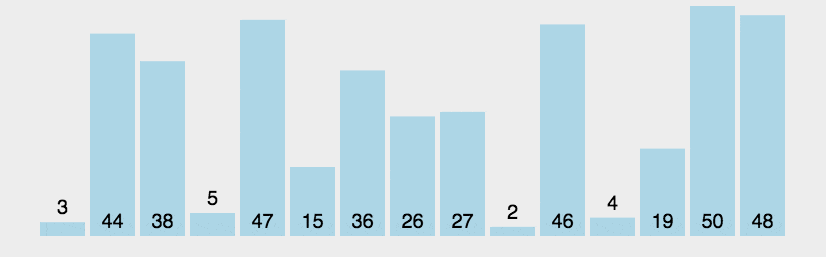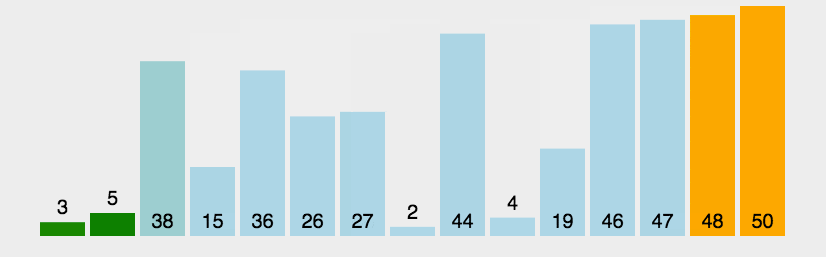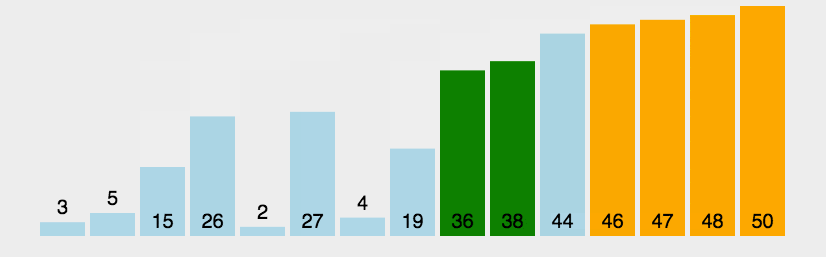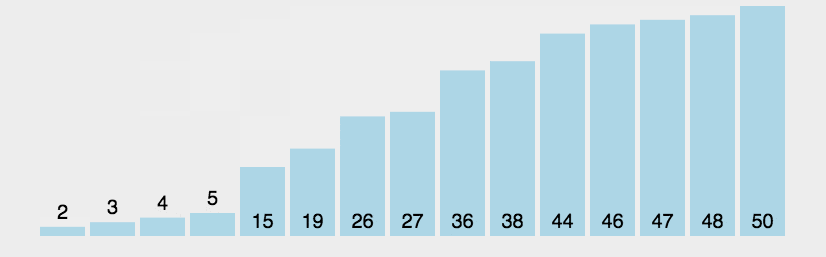一.算法时间复杂度定义
上一小节我们讲到,比较两个算法的优劣最重要的比较方式就是拿算法的时间复杂度来做比较.这节我们就来系统的学习一下算法的时间复杂度:
在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间.
一个算法所花费的时间与其中语句的总执行次数T(n)成正比例,算法中的基本操作的执行次数,为算法的时间复杂度.
二.大O阶渐近表示法
🎏大O阶渐近表示法的定义
一般情况下,算法中基本操作重复执行的次数T(n)是问题规模n的某个函数f(n),
算法的时间量度记作
T(n)=O(f(n))
它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称做算法的渐近时间复杂度,简称时间复杂度.
这样用大写O( )来体现算法时间复杂度的记法,我们称之为大O记法.
大O符号(Big O notation):是用于描述函数渐近行为的数学符号.
一般情况下,随着n的增大,T(n)增长最慢的算法为最优算法.
🎏推导大O阶方法
1.用常数1取代运行时间中的所有加法常数.
2.在修改后的运行次数函数中,只保留最高阶项.
3.如果最高阶项存在且不是1,则去除与这个项目相乘的常数.
经过上面这三步简单的操作后,得到的结果就是大O阶.
三.常见的时间复杂度
📌常数阶
我们首先来看顺序结构的时间复杂度.
如下算法,我们将一起分析上篇文章提到过的高斯算法为什么时间复杂度不是O(4),而是O(1).
int sum=0; /*执行一次*/ int n; /*执行一次*/ sum=(1+n)*n/2; /*执行一次*/ printf("%d",sum); /*执行一次*/
显而易见,这个算法的运行次数函数是f(n)=4.
根据我们推导大O阶的方法,第一步就是把常数项4改为1.在保留最高项时发现,它根本没有最高阶项,所以这个算法的时间复杂度为O(1).
接下来,我们试想一下,如果这个算法当中的语句"sum=(1+n)*n/2"有10句,即:
int sum = 0; /*执行第1次*/ int n ; /*执行第1次*/ sum = (1 + n) * n / 2; /*执行第1次*/ sum = (1 + n) * n / 2; /*执行第2次*/ sum = (1 + n) * n / 2; /*执行第3次*/ sum = (1 + n) * n / 2; /*执行第4次*/ sum = (1 + n) * n / 2; /*执行第5次*/ sum = (1 + n) * n / 2; /*执行第6次*/ sum = (1 + n) * n / 2; /*执行第7次*/ sum = (1 + n) * n / 2; /*执行第8次*/ sum = (1 + n) * n / 2; /*执行第9次*/ sum = (1 + n) * n / 2; /*执行第10次*/ printf("%d", sum); /*执行第1次*/
事实上,无论n为多少,上面的两段代码就是3次和13次执行的差异.
这种与问题的大小无关(n的多少),执行时间恒定的算法,我们称之为具有O(1)的时间复杂度,又叫常数阶.
注意:不管这个常数是多少,我们都记作O(1),而不是O(4),O(13)等其他任何数字,这是初学者常常犯的错误.
另外,对于分支结构而言(如:if...else...,switch...case)等,无论是真还是假,执行的次数都是恒定的,不会随着n的变大而发生变化.
所以单纯的分支结构(不包含在循环结构中),其时间复杂度也是O(1).
📌线性阶
线性阶的循环结构会复杂很多.要确定某个算法的阶次,我们常常需要确定某个特定语句或某个语句集运行的次数.因此,我们要分析算法的复杂度,关键就是要分析循环结构的运行情况.
如下面这段代码,它的总执行次数为2n+2次,按照推导大O阶方法,去掉最高项系数,去掉非最高项的项,我们得到该代码的时间复杂度为O(n).
要注意的是,对线性阶来讲,它最高项前的系数即便是999999999,我们在推导大O阶时也要将它去掉,只要它的系数是一个常数,那它的大O阶就是O(n).
int i = 0; /*执行一次*/ int n ; /*执行一次*/ for (i = 0; i < 2 * n; i++) { /*时间复杂度为O(1)的程序步骤序列*/ /*执行2*n次*/ }
📌对数阶
再来看下面这段代码:
int count = 1; /*执行一次*/ int n ; /*执行一次*/ while (count < n) { count = count * 2; /*执行"logn"次*/ }
由于每次count乘以2之后,就距离n更近了一分.count与多少个2相乘后大于n就会退出循环.
设循环内基本操作的循环次数为x,可得2^x=n,即�=log2�.
因此这个循环的时间复杂度为O(logn).
(tips:在数据结构中,时间复杂度如果为log2�,因为在计算机上不好表示这个函数,因此常常为了方便会简写为:logn.但这种简写仅限于以2为底的对数,其他的对数都不能用这种简写.)
📌平方阶
下面的例子是一个我们熟悉的二维数组:
int arr[10][10] = { 0 }; /*执行一次*/ int i = 0; /*执行一次*/ int j = 0; /*执行一次*/ int n ; /*执行一次*/ for (i = 0; i < n; i++) { for (j = 0; j < n; j++) { arr[i][j] = i + j; /*执行n*n次*/ } }
这段代码的总执行次数为n^2+4次,按照大O阶推导方法,去掉常数项,得到这段代码的时间复杂度为O(n^2).
这个例子中,如果外循环的循环次数改为了m,时间复杂度就变成O(m*n):
int arr[10][10] = { 0 }; /*执行一次*/ int i = 0; /*执行一次*/ int j = 0; /*执行一次*/ int n ; /*执行一次*/ int m ; /*执行一次*/ for (i = 0; i < m; i++) { for (j = 0; j < n; j++) { arr[i][j] = i + j; /*执行m*n次*/ } }
所以我们可得,循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数.
再来看看下面这个循环嵌套的时间复杂度:
int arr[10][10] = { 0 }; /*执行一次*/ int i = 0; /*执行一次*/ int j = 0; /*执行一次*/ int n = 10; /*执行一次*/ for (i = 0; i < n; i++) { for (j = i; j < n; j++) { arr[i][j] = i + j; /*执行?次*/ } }
这个程序循环执行的总次数可能不太好看出来,不过我们可以列个表计算一下:
| i的值 | 内循环执行的次数 |
| i=0 | n |
| i=1 | n-1 |
| i=2 | n-2 |
| ... | ... |
| i=n-2 | 2 |
| i=n-1 | 1 |
将i从0到n-1的每个内循环执行的次数加起来可得总的执行次数为:n+(n-1)+(n-2)+...+2+1=n*(n+1)/2=n^2/2+n/2.
根据大O阶推导方法可得,这段代码的时间复杂度为O(n^2).
📌调用函数的时间复杂度
再看下面这个例子:
int i = 0; /*执行一次*/ int j = 0; /*执行一次*/ int n; /*执行一次*/ for (i = 0; i < n; i++) { function(i); /*执行n次*/ }
上面这段代码中的for循环调用一个函数function:
void function(int count) { printf("%d",count); /*执行一次*/ }
因为function函数的时间复杂度是O(1).所以整体的时间复杂度为O(1)*O(n)=O(n).
而假如function是这样的:
void function(int count) { int j; for (j = 0; j < n;j++) { /*时间复杂度为O(1)的程序步骤序列*/ } }
很明显,这种情况下,function函数的时间复杂度是O(n).
所以整体的时间复杂度为O(n)*O(n)=O(n^2).
最后再看一个相对复杂的语句:
n++; /*执行一次*/ function(n); /*执行n次*/ int i; /*执行一次*/ int j; /*执行一次*/ for (i = 0; i < n:i++) /*执行n^2次*/ { function(i); } for (i = 0; i < n; i++) /* 执行n(n+1)/2次 */ { for (j = i; j < n; j++) { /*时间复杂度为O(1)的程序步骤序列*/ } }
function和上面一样:
void function(int count) { int j; for (j = 0; j < n;j++) { /*时间复杂度为O(1)的程序步骤序列*/ } }
可得,这个程序的执行次数T(n)=1+n+1+1+n^2+(n^2)/2+n/2=32�2+32�+3,根据推导大O阶的方法去掉系数和非最高阶项,最终这段代码的时间复杂度仍然是O(n^2).
📌常见的时间复杂度及其耗时排序
常见的时间复杂度
| 执行次数函数 | 阶 | 非正式术语 |
| 14 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
| 3n^2+2n+1 | O(n^2) | 平方阶 |
| 5log2�+20 | O(logn) | 对数阶 |
| 2�+3�log2�+19 | O(nlogn) | nlogn阶 |
| 6n^3+2n^2+3n+4 | O(n^3) | 立方阶 |
| 2^n | O(2^n) | 指数阶 |
常用的时间复杂度所耗费的时间从小到大依次是:
四.最坏情况与平均情况
我们先来分析一个我们熟悉的程序哈,冒泡排序程序:
void bubbleSort(int arr[], int n) { for (int i = 0; i < n - 1; i++) { for (int j = 0; j < n - i - 1; j++) { if (arr[j] > arr[j + 1]) { // 交换arr[j]和arr[j+1] int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; } } } } int main() { int arr[] = { 64, 34, 25, 12, 22, 11, 90 }; int n = sizeof(arr) / sizeof(arr[0]); bubbleSort(arr, n); printf("排序后的数组:\n"); for (int i = 0; i < n; i++) { printf("%d ", arr[i]); } return 0; }
冒泡排序逻辑图示如下:
我们假设我们要排序的数组是{9,8,7,6,5,4,3,2,1,0},而我们的目标是将它们排成升序,即{0,1,2,3,4,5,6,7,8,9}.
计算一下这种情况下程序的运行次数(因为交换元素的三步操作的时间复杂度是O(1),所以我们将它们视为执行1次):9+8+7+6+5+4+3+2+1=45次.
由此易得出,当数组元素个数为n时,冒泡排序的执行次数函数T(n)=n*(n+1)/2.
你有没有发现一个问题,如果冒泡排序的待排序数组是{9,8,7,6,5,4,3,2,1,0},而我们的目标排序数组是{0,1,2,3,4,5,6,7,8,9},那简直是太"倒霉了",就像你为了参加公司组团夏天去夏威夷旅游买了好多短袖,短裤,墨镜,泳衣等装备,而最后公司却决定冬天去哈尔滨旅游一样.其实这种情况就是程序运行时间的最坏情况.
相应的,程序运行时间也会有最好情况,最好情况就是,冒泡排序的待排序数组是{9,8,7,6,5,4,3,2,1,0},而我们的目标数组也是{9,8,7,6,5,4,3,2,1,0},那程序运行的次数就是0次,这就是程序运行时间的最好情况.
但现实生活中,我们大部分遇到的数据都没有这么极端,根据正态分布原则,反而是只需要排最坏次数一半的次数出现的可能性大一些.我们将这种情况称为平均时间复杂度.
平均时间是所有情况中最有意义的,因为他是期望的运行时间.
对算法的分析,一种方法是计算所有情况的平均值,这种时间复杂度的计算方法称为平均时间复杂度.
另一种方法是计算最坏情况下的时间复杂度,这种方法称为最坏时间复杂度.
知道了这两种方法之后,我们还需要做一件事,就是要考虑在实际运用中到底选择这两个哪个复杂度作为衡量算法好坏的时间复杂度.
其实,在应用中,除非特殊指定,我们提到的运行时间都是最坏情况的运行时间.
因为最坏情况运行时间是一种保证,那就是运行时间将不会再坏了.
不好理解的话,我举个例子:
假如你和女朋友约好今天下午在图书馆约会,你估计自己大概1-3点之间能到达约会的目的地,这时候你的女朋友问你约会时间定在几点,你会和她说1点还是2点还是3点?
如果定在一点,那你有2/3的概率会迟到,如果定在2点,那你还是有1/3的概率会迟到,一旦迟到,就将给女孩子留下很不好的印象.
所以我们最好还是将时间定在3点,因为这是一种保证,就是再迟,也不会比三点还迟了.
对算法运行时间的估量也是这个道理,再加上在很多情况下,各种输入数据集出现的概率难以确定,算法的平均时间复杂度也就难以计算.
因此在实际中一般情况我们关注的是算法的最坏运行情况.
结语
当我们搞清楚什么是算法的时间复杂度后,在数据结构算法篇,我们还将一起学习算法的空间复杂度及算法效率的度量方法相关的知识.希望这些内容能对大家有所帮助,一起学习,一起进步!