Dijkstra算法虽然好,但是它不能解决带有负权边(边的权值为负数)的图。接下来
介绍一个无论是思想上还是代码实现上都堪称完美的最短路算法:Bellman-Ford。
Bellman-Ford算法非常简单,核心代码只有4行,并且可以完美地解决带有负权边的图.
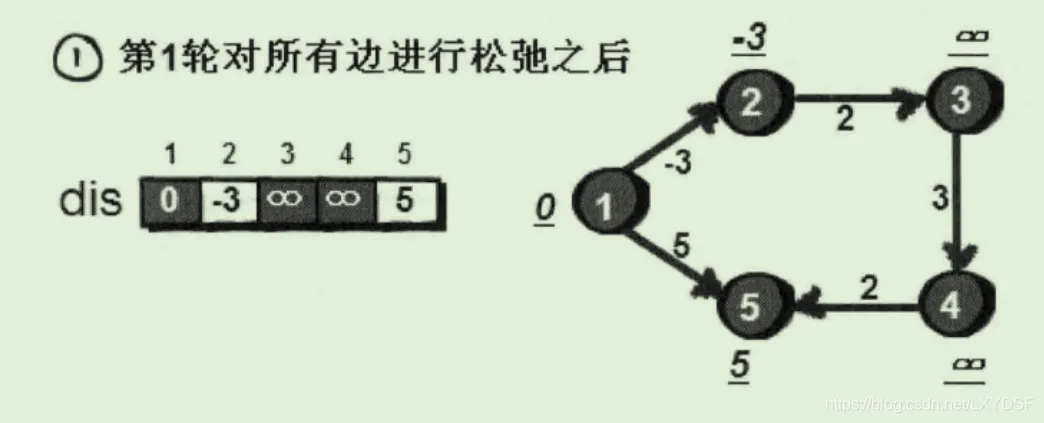
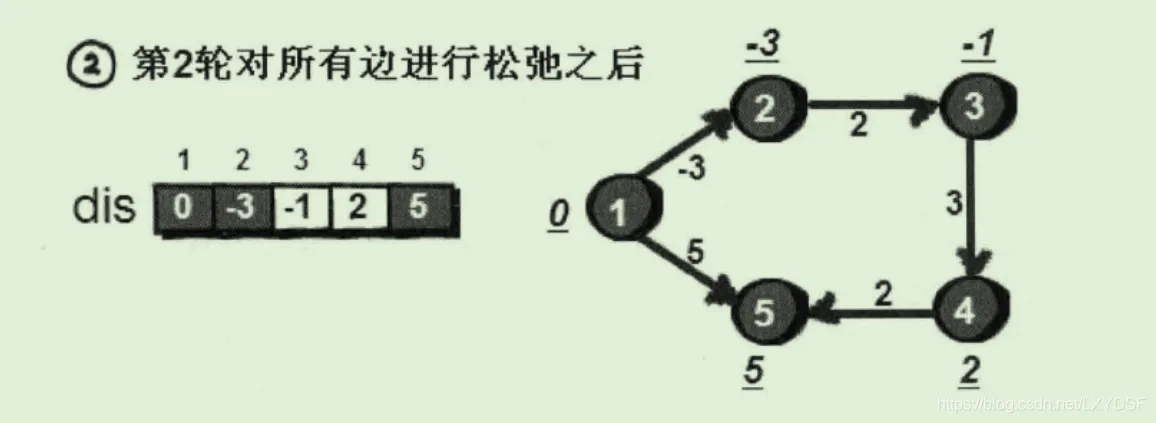
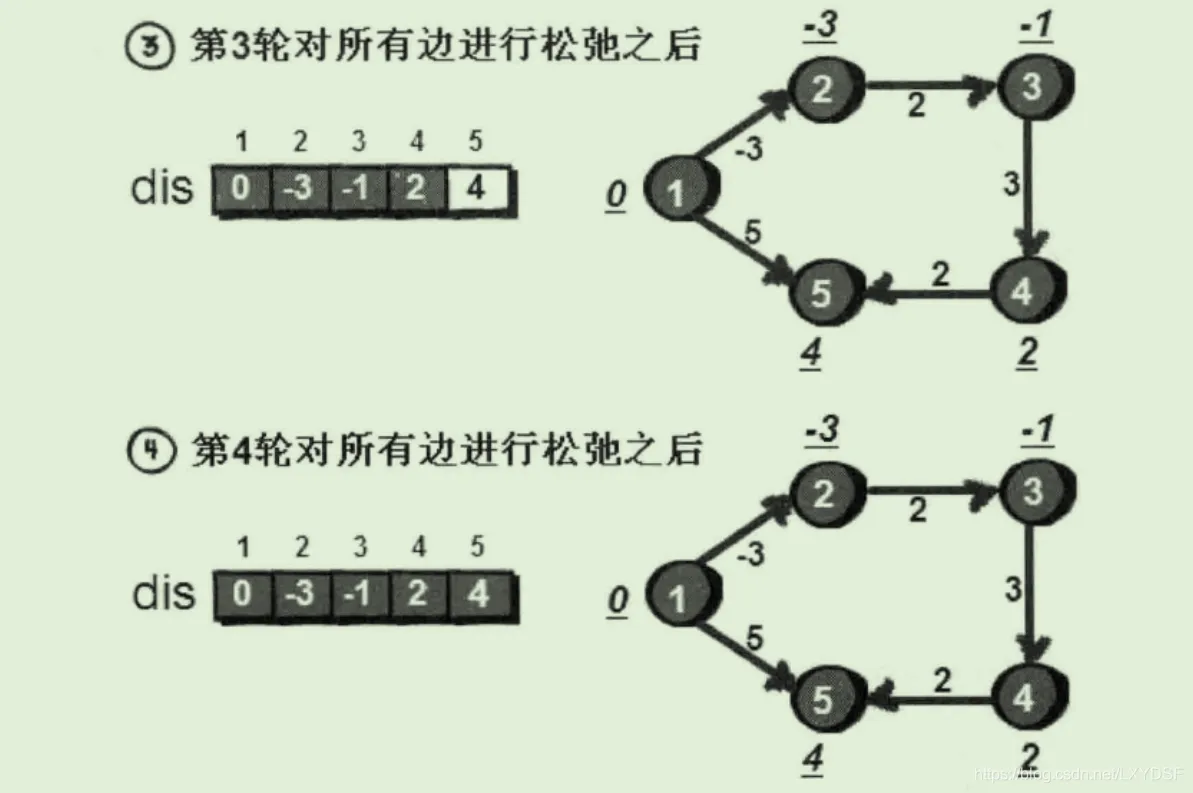
思路 : 一张有向图,有n个点,m条边,用dis[]数组保存源点到各点的最短距离,可以通过对边进行n-1次的遍历,当其满足dis[v]>dis[u]+w的时候,就对其进行松弛更新,重复n-1次以后就能得到答案,如果n-1次以后还能继续更新,则可以判断图中出现了负权环,思路非常简短。
举例验算:
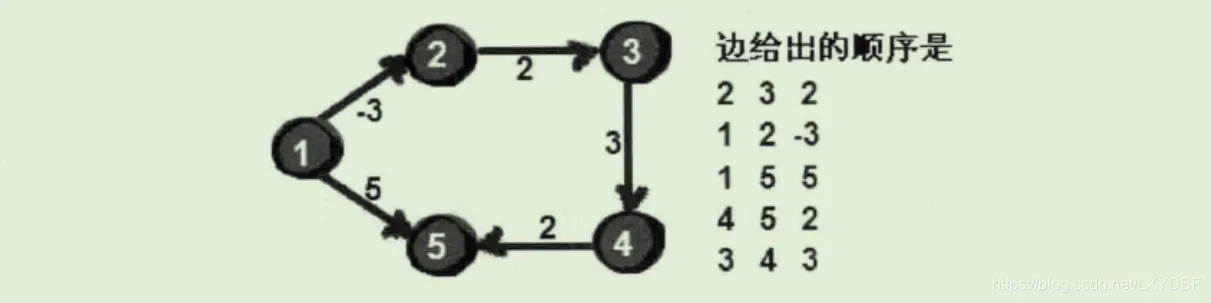
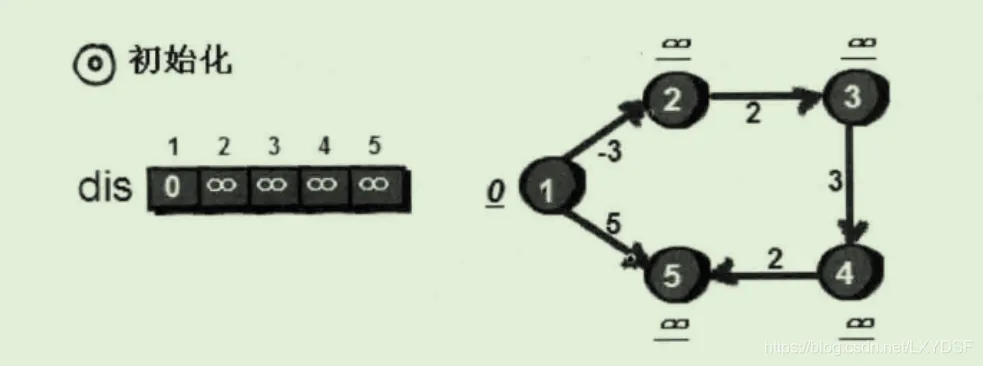
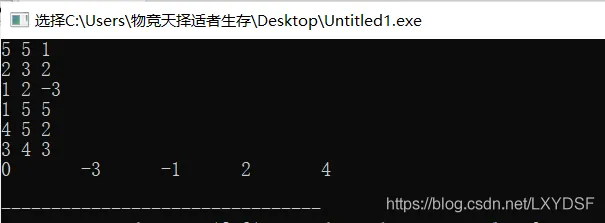
1.例图和边输入的顺序如下,并对dis数组进行初始化
另外实现这个算法的数据结构是边集数组.因为我们需要存储起始点,终点,权值.从而对每条边进行松弛.
参考代码
#include<iostream> #include<queue> using namespace std; const int maxn = 1000; const int INF = 0x3f3f3f3f; int u[maxn],v[maxn],w[maxn],dis[maxn],flag;//dis:从起始点到当前点的最短路径 int n,m,x;//n:顶点数 m:边数 x:起始点 void Ford(int s){ for(int i = 1; i <= n; i++){//dis数组进行初始化 dis[i] = INF; } dis[s] = 0; for(int i = 0; i < n-1;i++){// flag = 0;//flag:用于标记此次是否所有边是否进行松弛了. for(int j = 0; j < m; j++){ if(dis[v[j]]>=dis[u[j]]+w[j]){ dis[v[j]] = dis[u[j]]+w[j]; flag = 1; } } if(!flag){//如果 这次没有进行松弛,说明所有的点 都已松弛完毕. break; } } } int main() { cin>>n>>m>>x; for(int i = 0; i<m; i++) { cin>>u[i]>>v[i]>>w[i]; } Ford(x); for(int i = 1; i <= n; i++){ cout<<dis[i]<<"\t"; } cout<<endl; return 0; }
运行结果:
Ford算法还可以去检测一个图是否有负权回路,如果在进行n-1轮松弛后,仍然存在:
if(dis[v[i]] > dis[u[i]] + w[i]) dis[v[i]] = dis[u[i]] + w[i];
则说明存在负环回路.
SPFA算法
思路: SPFA算法就是用队列优化过的Bellman-Ford算法,初始时将源点加入队列。每次选出队首结点,对其的所有出边进行松弛更新,更新成功的点加入队列,同一个结点可能被多次更新,但是同一个结点只能在同时在队列中出现一个,重复这个操作直到队列为空.
参考代码
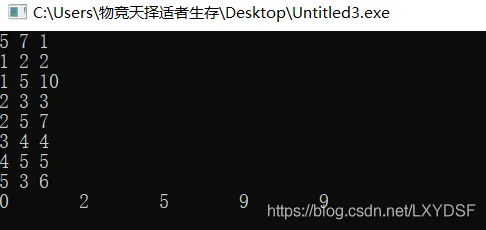
#include<iostream> #include<queue> using namespace std; const int maxn = 100; const int INF = 0x3f3f3f3f; int n,m,s,c,num; int head[maxn],dis[maxn],vis[maxn];//vis:标记节点是否在队列中 struct node{ int next,to,w; }e[maxn*maxn]; void add(int u,int v,int cc){ e[++num].next = head[u]; e[num].to = v; e[num].w = cc; head[u] = num; } void spfa(int u){ for(int i = 1; i <= n; i++){//dis进行初始化. dis[i] = INF; } queue<int> q; q.push(u); vis[u] = 1; dis[u] = 0; while(!q.empty()){ int x = q.front(); q.pop();//怕最后忘记弹出,直接在这里处理吧.. vis[x] = 0; for(int i = head[x]; i; i=e[i].next){ if(dis[e[i].to] > dis[x]+e[i].w){//如果该边可以松弛 dis[e[i].to] = dis[x]+e[i].w;//dis更新 if(!vis[e[i].to]) { q.push(e[i].to); vis[e[i].to] = 1; } } } } } int main() { int u,v,w; cin>>n>>m>>s; for(int i = 0; i < m; i++){ cin>>u>>v>>w; add(u,v,w); } spfa(s); for(int i = 1; i<=n;i++){ cout<<dis[i]<<"\t"; } cout<<endl; return 0; } /* 5 7 1 1 2 2 1 5 10 2 3 3 2 5 7 3 4 4 4 5 5 5 3 6 */
运行结果:
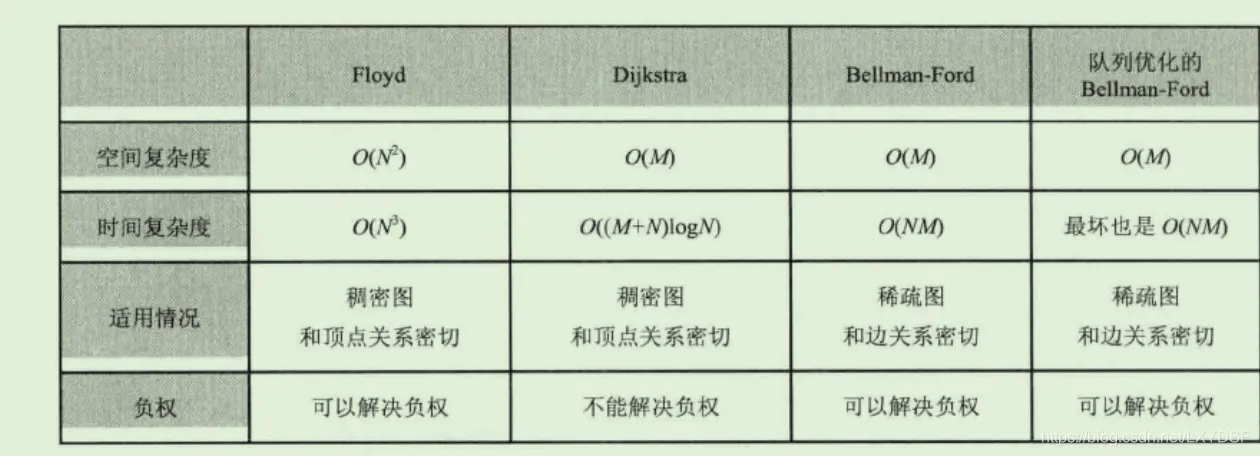
最短路径算法分析
对于判断正环或者负环的问题,我们可以使用Ford,SPFA,或者DFS(判断能否回到曾经搜过的点).