RGB Triplets
题目描述
We have a string S of length N consisting of R, G, and B.
Find the number of triples (i, j, k) (1≤i<j<k≤N) that satisfy both of the following conditions:
·Si≠Sj, Si≠Sk, and Sj≠Sk.
·j−i≠k−j.
Constraints
·1≤N≤4000
·S is a string of length N consisting of R, G, and B.
输入
Input is given from Standard Input in the following format:
N
S
输出
Print the number of triplets in question.
样例输入 Copy
【样例1】
4 RRGB
【样例2】
39 RBRBGRBGGBBRRGBBRRRBGGBRBGBRBGBRBBBGBBB
样例输出 Copy
【样例1】
1
【样例2】
1800
提示
样例1解释:
Only the triplet (1, 3, 4) satisfies both conditions. The triplet (2, 3, 4) satisfies the first condition but not the second, so it does not count.
组合数学
从只含有RGB三个字符的字符串中挑选出满足条件的三元组数量满足 (i, j, k) (1≤i<j<k≤N)
·Si≠Sj, Si≠Sk, and Sj≠Sk.
·j−i≠k−j.
typedef int itn; int n, m; ll a[maxn]; ll pre[maxn]; ll dp[maxn]; int main() { cin >> n; string s; cin >> s; ll cntr = 0, cntg = 0, cntb = 0; for (int i = 0; i < n; i++) { if (s[i] == 'R') cntr ++; else if (s[i] == 'G') cntg ++; else cntb ++; } ll ans = cntb * cntg * cntr; for (int i = 0; i <= n - 3; i++) { // len == 3 3-3==0 1, 2 for (int j = i + 1; j <= n - 2; j++) {// len == 3 3-2 == 1 0 1 2 int p = 2 * j - i; if (p >= n) break; if (s[i] != s[j] && s[i] != s[p] && s[j] != s[p]) --ans; } } cout << ans << endl; return 0; } /* 4 RRGB 39 RBRBGRBGGBBRRGBBRRRBGGBRBGBRBGBRBBBGBBB */
Select Half
题目描述
Given is an integer sequence A1,…,AN of length N.
We will choose exactly ⌊N/2⌋ elements from this sequence so that no two adjacent elements are chosen.
Find the maximum possible sum of the chosen elements.
Here ⌊x⌋ denotes the greatest integer not greater than x.
Constraints
·2≤N≤2×105
·|Ai|≤109
·All values in input are integers.
输入
Input is given from Standard Input in the following format:
N
A1 … AN
输出
Print the maximum possible sum of the chosen elements.
样例输入 Copy
【样例1】
6 1 2 3 4 5 6
【样例2】
5 -1000 -100 -10 0 10
【样例3】
10 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
【样例4】
27 18 -28 18 28 -45 90 -45 23 -53 60 28 -74 -71 35 -26 -62 49 -77 57 24 -70 -93 69 -99 59 57 -49
样例输出 Copy
【样例1】
12
【样例2】
0
【样例3】
5000000000
【样例4】
295
提示
样例1解释:Choosing 2, 4, and 6 makes the sum 12, which is the maximum possible value.
在n个数中选择n/2个数,下取整,选择的数不能相邻,比如选择了i号位置的数字之后,i-1以及i+1都不能选择
dp前缀和优化
typedef int itn; int n, m; ll a[maxn]; ll pre[maxn]; ll dp[maxn]; int main() { cin >> n; for (int i = 1; i <= n; i++) { a[i] = read; if (i == 1) pre[i] = a[i]; else pre[i] = pre[i - 2] + a[i]; } for (int i = 2; i <= n; i++) { if (i % 2) dp[i] = max(dp[i - 1], dp[i - 2] + a[i]); else dp[i] = max(dp[i - 2] + a[i], pre[i - 1]); } cout << dp[n] << endl; return 0; }
心灵的抚慰
题目描述
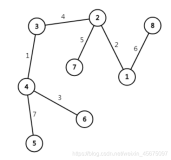
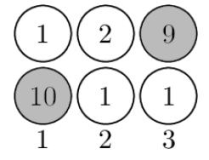
病毒问题解决后,神牛们的心灵久久不能平静。他可以从一个程序联想到一些相似的程序。比如从程序1联想到2,从2联想到4,从4联想到6,从6联想到9……就像搜索一样一步一步越陷越深。不过同一种联想他只会联想一次。比如1、2之间他进行了一次联想,那么他不会再重新联想1到2,或2到1。如果他刚开始时想到的程序能够经过联想若干次后联想回到原程序,那不就乱回来了吗?由于神牛马上就要开乱,请在1秒内告诉他,他需要想哪个程序,以便乱回来。
给出一些程序和他们互相联想的关系(如果两个程序A、B有联系,神牛可以从A联想到B,也可以从B联想到A,但A、B之间神牛最多联想一次),请告诉神牛他需要想哪个程序,以便在最短的时间内乱回来,并输出这个最短时间。
输入
第一行有两个正整数N,M,分别表示程序个数和有多少对程序可以被神牛直接互相联想。
以下M行,每行三个正整数,分别表示一种联想的两端的程序的编号(从1开始),以及进行这种联想所需要的最短时间(≤3500)。
输出
如果神牛无论如何都再也乱不回来了,输出“He will never come back.”。
如果神牛能够乱回来,请输出神牛会乱多长时间。
样例输入 Copy
4 3 1 2 10 1 3 20 1 4 30
样例输出 Copy
He will never come back.
提示
对于100% 的数据,n≤250。
弗洛伊德求最小环
int n, m; ll dis[307][307]; ll val[307][307]; ll ans = INF; int main() { cin >> n >> m; for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) dis[i][j] = INF, val[i][j] = INF; } for (int i = 1; i <= m; i++) { ll u = read, v = read, w = read; val[u][v] = min(val[u][v], w); val[v][u] = min(val[v][u], w); dis[u][v] = min(dis[u][v], val[u][v]); dis[v][u] = min(dis[v][u], val[v][u]); } for (int k = 1; k <= n; k++) { for (int i = 1; i <= k - 1; i++) { for (int j = 1 + i; j <= k - 1; j++) { ans = min(ans, dis[i][j] + val[j][k] + val[k][i]); } } for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]); } } } if (ans == INF) puts("He will never come back."); else cout << ans << endl; return 0; } /* 4 3 1 2 10 1 3 20 1 4 30 */