积分解多条曲线围成面积且具有不同边界MATLAB

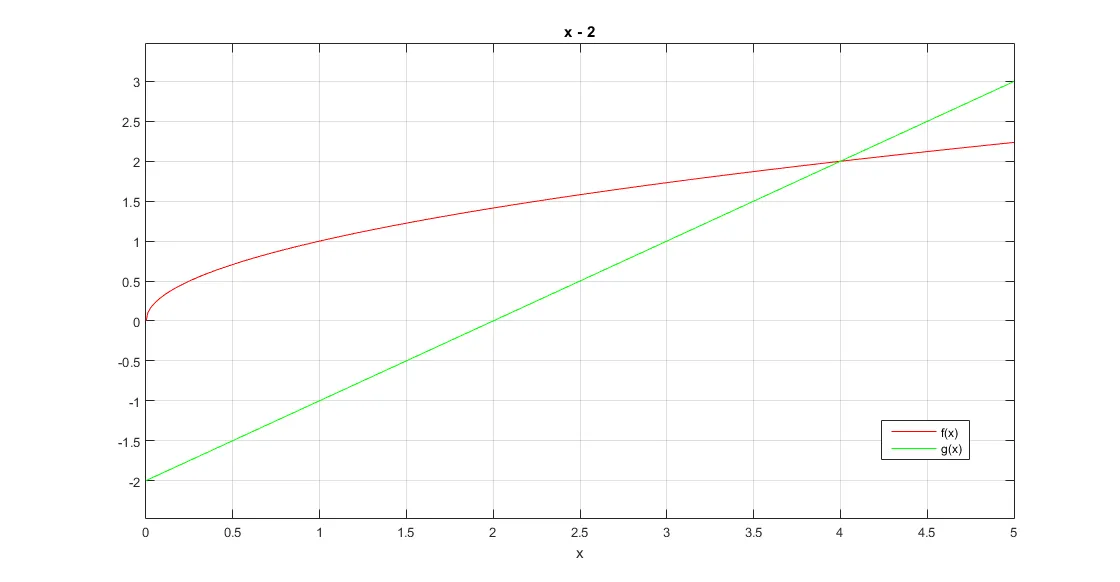
(第一部分面积)s1: f(x)=x^(1/2)在[0,2]区间内与x坐标轴围成的面积。直接计算f(x)dx在[0,2]的积分面积。
(第二部分面积)s2: f(x)=x^(1/2)与g(x)=x-2在区间[2,4]围成的面积。这一部分面积可由(f(x)-g(x))dx积分解出,积分下限是2,上限是4。
MATLAB代码:
syms x f g F;
f=x.^(1/2);
e1=ezplot(f,[0,5]);
set(e1,'Color','r','LineWidth',0.5);
hold on;
g=x-2;
e2=ezplot(g,[0,5]);
set(e2,'Color','g','LineWidth',0.5);
hold on;
grid on;
s1=int(f,[0,2]);
F=f-g;
s2=int(F,[2,4]);
S=s1+s2
S =
10/3图:
计算得到总面积:
10/3