题目描述

输入一个 非空 整型数组，数组里的数可能为正，也可能为负。

数组中一个或连续的多个整数组成一个子数组。

求所有子数组的和的最大值。

要求时间复杂度为 O(n)。

数据范围

数组长度 [1,1000]。

数组内元素取值范围 [−200,200]。

样例

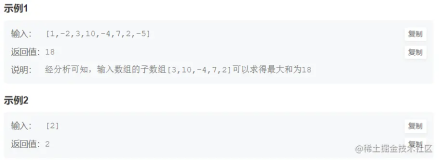
输入：[1, -2, 3, 10, -4, 7, 2, -5]
输出：18

方法一：贪心 O(n)

这道题可以这么想：

由于数组中存在负数，所以 ans 要初始化为负无穷，然后用 cnt 来保存当前遍历的累加和。

判断 cnt 是否小于 0 ，如果小于 0 就将它置为 0 。

cnt 加上当前遍历到的数，然后与 ans 进行比较，如果出现更大的值就更新。

我们拿题目的样例举例，来看看具体是如何实现的：

第一步： 先初始化 cnt = 0 ，且 ans = INT_MIN 。

第二步： 将 1 加入 cnt ，发现 cnt 比 ans 大，更新答案 ans 。

第三步： 将 -2 加入 cnt ，发现 cnt 小于 0 ，故将 cnt 置 0 。

第四步 ~ 第九步： 重复上述操作，不断更新答案。

第十步： 返回最终答案 ans 。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int cnt = 0, ans = INT_MIN;
        for (auto x : nums)
        {
            if (cnt < 0)  cnt = 0;
            cnt += x;
            ans = max(ans, cnt);
        }
        return ans;
    }
};

欢迎大家在评论区交流~