堆排序
堆排序的思想
堆排序是用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
以大顶堆为例,现将列表构造成一个大顶堆,此时,整个列表的最大值就是堆顶的值。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序列表了。具体可以总结为下面的三个步骤:
- 将无序列表构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
- 将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
- 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个列表有序。
图解堆排序
在了解堆排序之前我们需要先了解堆的概念。对于堆结构我们可以分为大顶堆和小顶堆两种:
- 大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;
- 小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;
大顶堆和小顶堆的结构如下所示:

了解了大顶堆和小顶堆的含义之后,我们开始了解堆排序的过程,首先给出如下的一个无序列表,我们用堆的形式来表示这个列表。
- 第一步:将无序列表构建成一个大顶堆
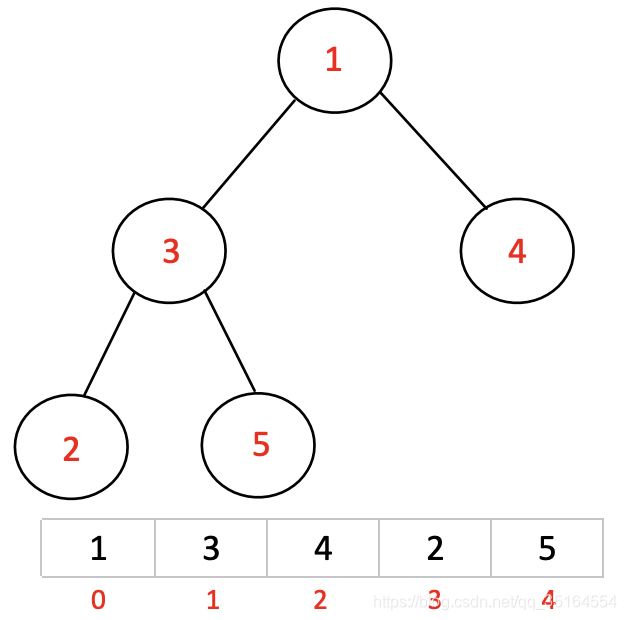
对于这个堆我们的目的是构造出一个大顶堆,构造的过程中我们需要不断的比较每一个堆结构的大小关系,并切把大的元素调整为父节点,对于325三个元素组成的子堆举例: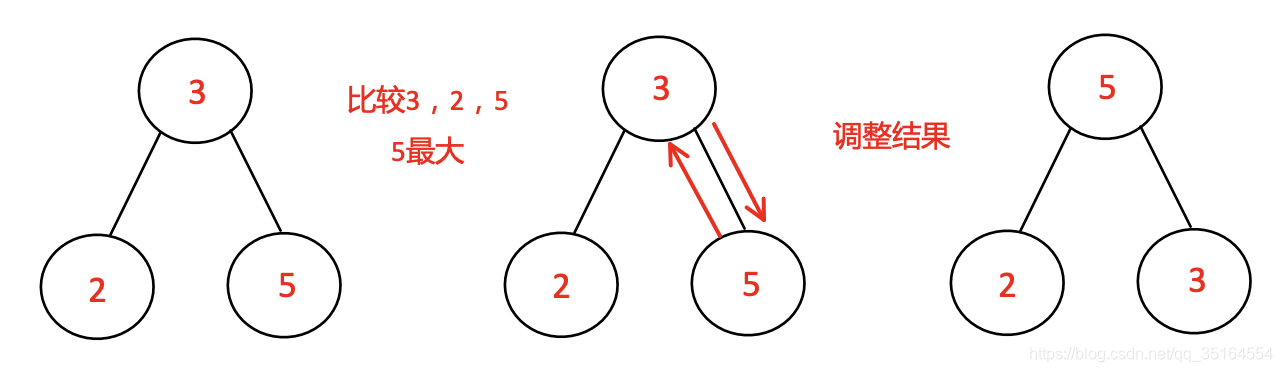
经过上述子堆的调整后,原堆的结构如下:
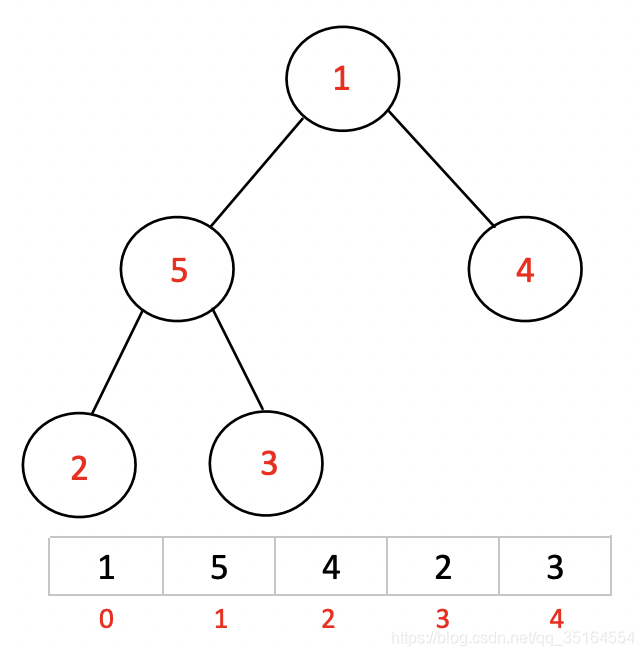
继续用上述方法调整154三个元素组成的子堆:
经过本次调整之后,我们发现整个堆的堆顶(5)已经是最大的了,但是调整之后的子堆123又变的混乱了,此时我们再一次对该子堆做调整:
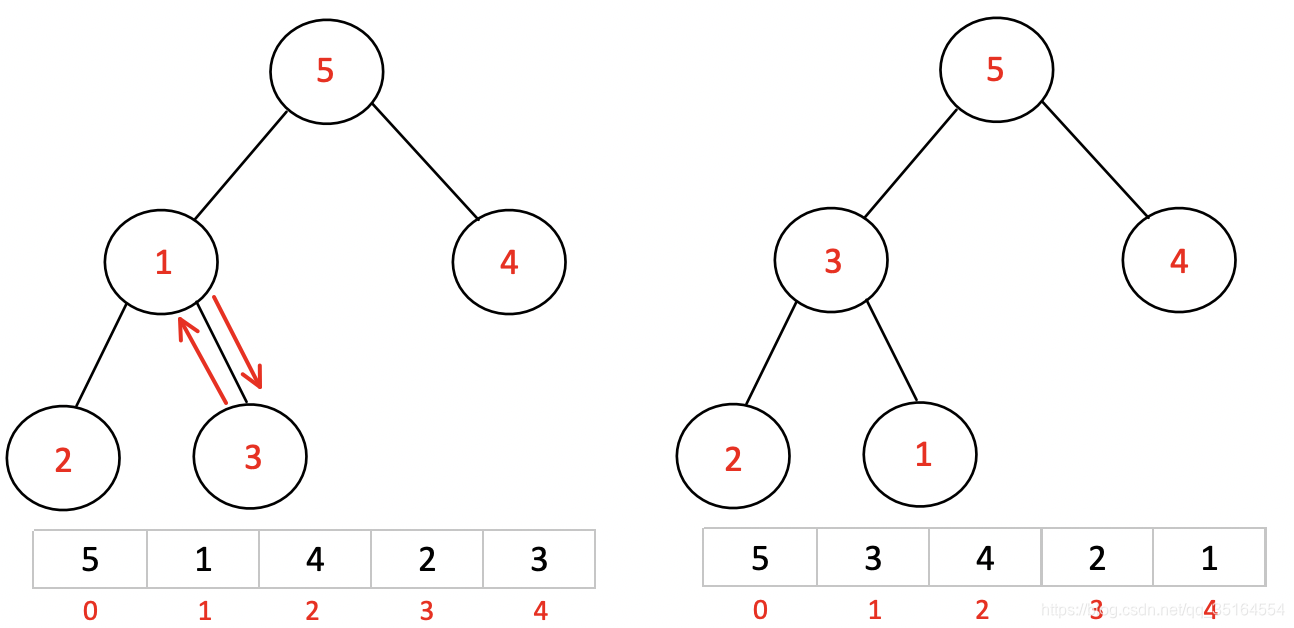
至此我们把最开始的无序列表构造成了一个大顶堆,接下来就要进行排序的操作了。
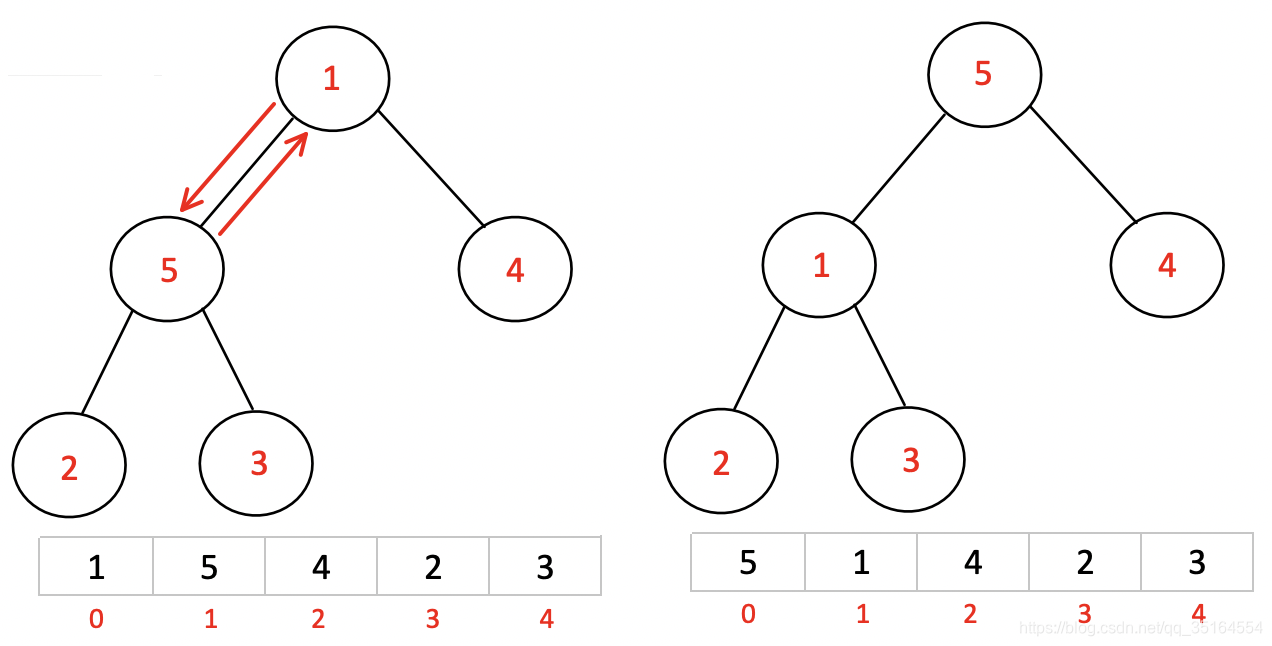
- 第二步:将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
首先我们将堆顶元素5和末尾元素1做交换:
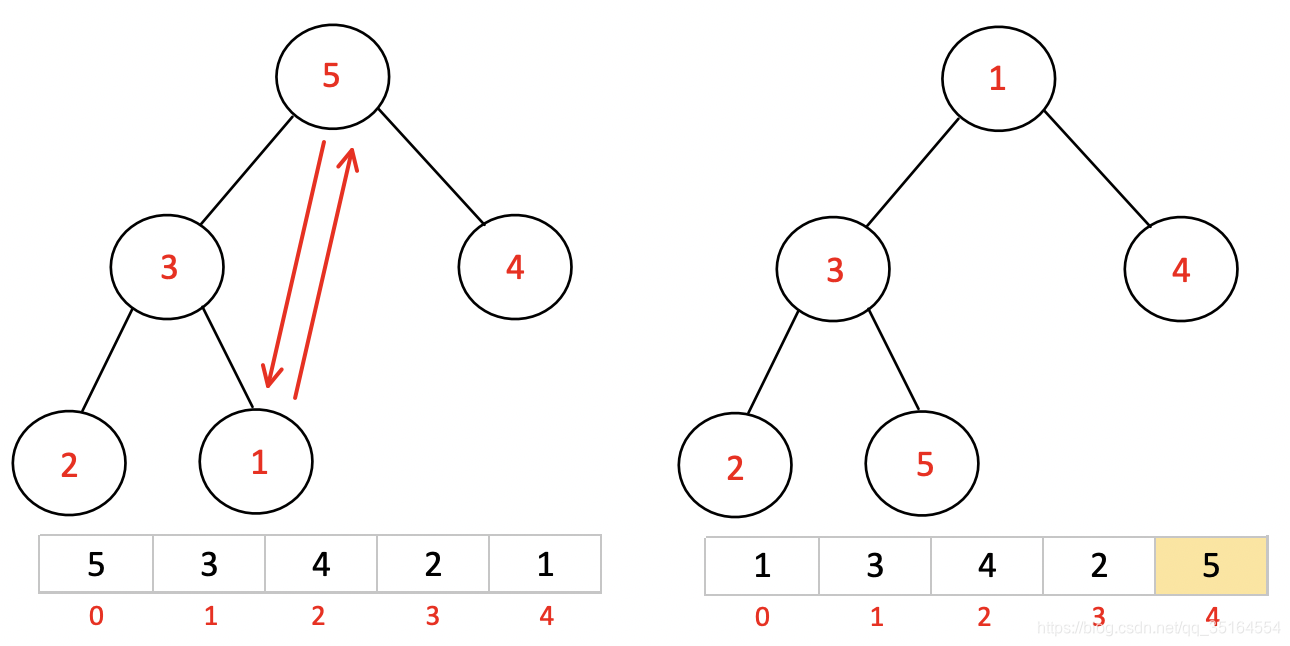
进行完本次操作我们可以发现最大的元素5就被放倒了最后的位置,此时我们把5先抛除。
- 第三步:重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个列表有序。
对于剩下的列表[1342]继续按照第一步的方法构造出大顶堆,然后按照第二步的方法继续找到最大的元素即可,直到排序完成: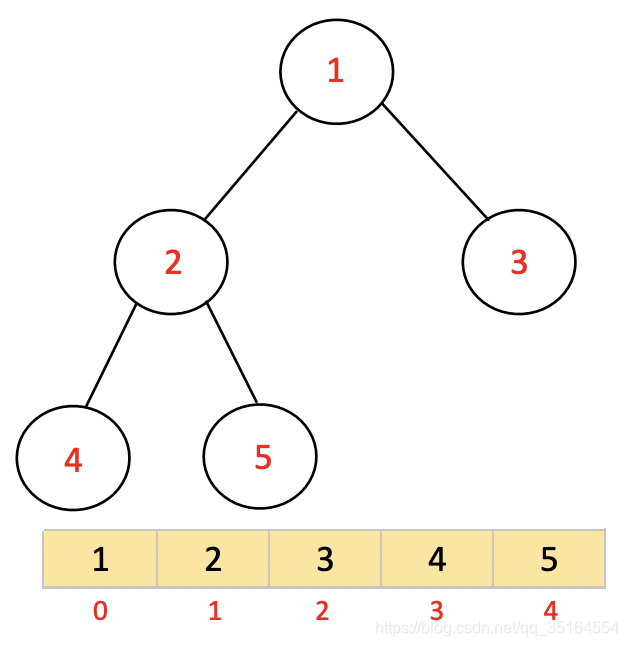
堆排序的性质
最优时间复杂度:$O(nlog_2n)$
最坏时间复杂度:$O(nlog_2n)$
稳定性:不稳定
堆排序的代码实现
lst = list(map(int, input().split(',')))
# 创建堆(调整堆)
def heapify(arr, n, i):
largest = i
l = 2 * i + 1 # left = 2*i + 1
r = 2 * i + 2 # right = 2*i + 2
if l < n and arr[i] < arr[l]:
largest = l
if r < n and arr[largest] < arr[r]:
largest = r
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
# 堆排序
def heapSort(arr):
n = len(arr)
# Build a maxheap.
for i in range(n, -1, -1):
heapify(arr, n, i)
# 一个个交换元素
for i in range(n - 1, 0, -1):
arr[i], arr[0] = arr[0], arr[i]
heapify(arr, i, 0)
return arr
heapSort(lst)
