✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
⛄ 内容介绍
本文介绍了一种新的群体智能策略——抗冠状病毒优化(ACVO)算法。该算法是一种多智能体策略,其中每个智能体都是一个人,通过观察控制协议试图保持健康并减缓 COVID-19 的传播。该算法由三个主要步骤组成:社交距离、隔离和隔离。在社交距离阶段,算法试图保持人与人之间的安全物理距离并限制密切接触。在隔离阶段,算法隔离疑似人员以防止疾病传播。应该照顾一些没有遵守健康协议并感染病毒的人,以使其完全康复。在隔离阶段,算法关心感染者恢复健康。该算法迭代地将这些算子应用于人群,以找到最适合和最健康的人。所提出的算法在标准多变量单目标优化问题上进行了评估,并与几种对应算法进行了比较。结果表明,与同类产品相比,ACVO 在大多数测试问题上的优势。
⛄ 部分代码
function [fobj, l, u, g, d]=GetBenchmarkFunction(number)
dim=30;
switch number
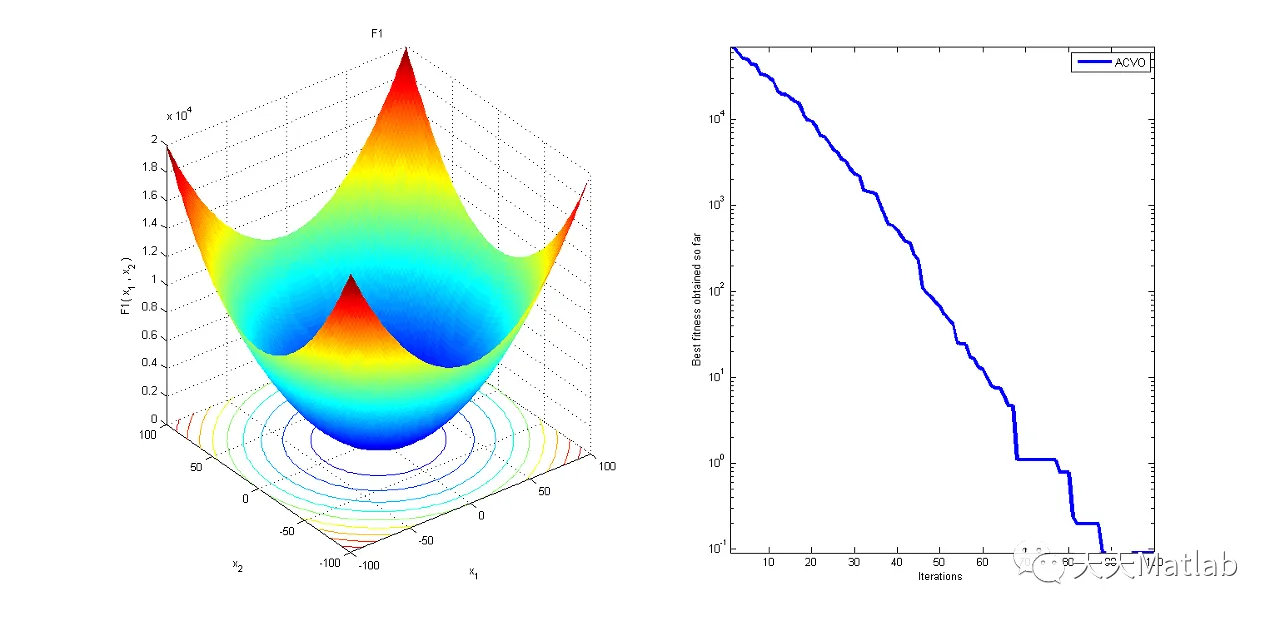
case 'F1'
% F1- Sphere lower=[-100], upper=[100], gminimum=[0]
fobj = @F1;
l=[-100];
u=[100];
g=0;
d=dim;
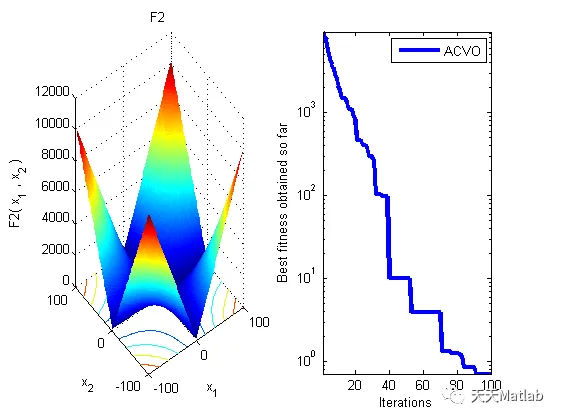
case 'F2'
% F2- SumSquares lower=[-10], upper=[10], gminimum=[0]
fobj = @F2;
l=[-10];
u=[10];
g=0;
d=dim;
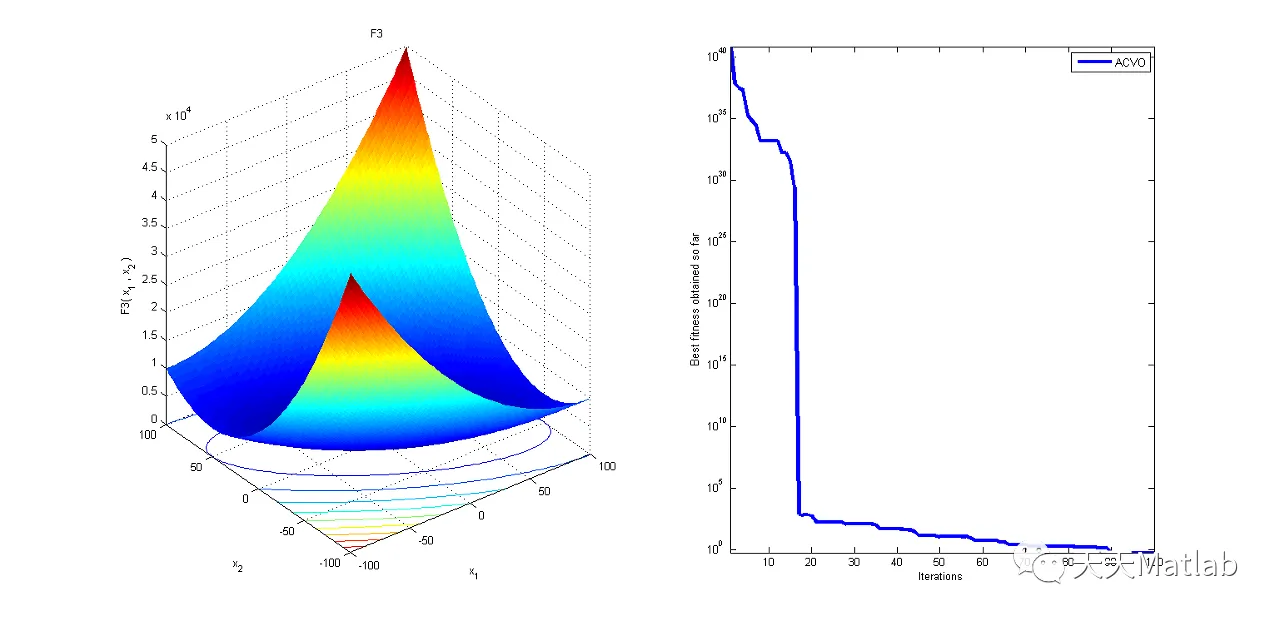
case 'F3'
% F3- Schwefel 2.22 lower=[-100], upper=[100], gminimum=[0]
fobj = @F3;
l=[-100];
u=[100];
g=0;
d=dim;
case 'F4'
% F4- Rastrigin lower=[-5.12], upper=[5.12] gminimum=[0]
fobj = @F4;
l=[-5.12];
u=[5.12];
g=0;
d=dim;
case 'F5'
% F5- Alpine lower=[0], upper=[10] gminimum=[0]
fobj = @F5;
l=[0];
u=[10];
g=[0];
d=dim;
case 'F6'
% F6- Griewank lower=[-600], upper=[600] gminimum=[0]
fobj = @F6;
l=[-600];
u=[600];
g=[0];
d=dim;
case 'F7'
% F7- Penalized lower=[-50], upper=[50] gminimum=[0]
fobj = @F7;
l=[-50];
u=[50];
g=[0];
d=dim;
case 'F8'
% F8- Ackley lower=[-32], upper=[32] gminimum=[0]
fobj = @F8;
l=[-32];
u=[32];
g=[0];
d=dim;
case 'F9'
% F9- Shubert lower=[-10], upper=[10] gminimum=[-186.73]
fobj = @F9;
l=[-10];
u=[10];
g=[-187];
d=dim;
case 'F10'
% F10- Bohachevsky lower=[-5], upper=[5] gminimum=[0]
fobj = @F10;
l=[-5];
u=[5];
g=[0];
d=dim;
end
end
function z = F1(x)
% F1- Sphere lower=[-100], upper=[100], gminimum=[0]
z=sum(x'.^2)';
end
function z = F2(x)
% F2- SumSquares lower=[-10], upper=[10], gminimum=[0]
[m, n] = size(x);
x2 = x .^2;
I = repmat(1:n, m, 1);
z = sum( I .* x2, 2);
end
function z = F3(x)
% F3- Schwefel 2.22 lower=[-100], upper=[100], gminimum=[0]
absx = abs(x);
z = sum(absx, 2) + prod(absx, 2);
end
function z = F4(x)
% F4- Rastrigin lower=[-5.12], upper=[5.12] gminimum=[0]
n = size(x, 2);
A = 10;
z = (A * n) + (sum(x .^2 - A * cos(2 * pi .* x), 2));
end
function z = F5(x)
% F5- Alpine 1 lower=[0], upper=[10] gminimum=[0]
z = sum(abs(x .* sin(x) + 0.1 * x), 2);
end
function z = F6(x)
% F6- Griewank lower=[-600], upper=[600] gminimum=[0]
n = size(x, 2);
sumcomp = 0;
prodcomp = 1;
for i = 1:n
sumcomp = sumcomp + (x(:, i) .^ 2);
prodcomp = prodcomp .* (cos(x(:, i) / sqrt(i)));
end
z = (sumcomp / 4000) - prodcomp + 1;
end
function z = F7(x)
% F7- Penalized lower=[-50], upper=[50] gminimum=[0], dim=30
a=10;
k=100;
m=4;
d=size(x,2);
for i=1:size(x,1)
xi=x(i,:);
term4=0;
for j=1:d
if xi(j)>a
u1=k*(xi(j)-a).^m;
elseif xi(j)<(-a)
u1=k*(-xi(j)-a).^m;
else
u1=0;
end
term4=term4+u1;
end
for k=1:d
yi(k)=1+0.25*(xi(k)+1);
end
term1=10*(sin(pi*yi(1))^2);
term2=0;
for k2=1:d-1
term2=term2+(((yi(k2)-1).^2)*(1+10*(sin(pi*yi(k2+1))).^2));
end
term3=(yi(d)-1)^2;
z(i)=pi/d* (term1+ term2+ term3)+ term4;
end
z=z';
end
function z = F8(x)
% F8- Ackley lower=[-32], upper=[32] gminimum=[0]
n = size(x, 2);
ninverse = 1 / n;
sum1 = sum(x .^ 2, 2);
sum2 = sum(cos(2 * pi * x), 2);
z = 20 + exp(1) - (20 * exp(-0.2 * sqrt( ninverse * sum1))) - exp( ninverse * sum2);
end
function z = F9(x)
% F9- Shubert lower=[-10], upper=[10] gminimum=[-186.73]
x1 = x(:,1);
x2 = x(:,2);
sum1 = 0;
sum2 = 0;
for ii = 1:5
new1 = ii * cos((ii+1)*x1+ii);
new2 = ii * cos((ii+1)*x2+ii);
sum1 = sum1 + new1;
sum2 = sum2 + new2;
end
z = sum1 .* sum2;
end
function z = F10(x)
% F10- Bohachevsky lower=[-5], upper=[5] gminimum=[0]
n = size(x, 2);
Y = x(:, 2);
X = x(:, 1);
z = X.^2 + Y.^2 + (25 * (sin(X).^2 + sin(Y).^2));
end
⛄ 运行结果
⛄ 参考文献
Emami, Hojjat. “Anti-Coronavirus Optimization Algorithm.” Soft Computing, vol. 26, no. 11, Springer Science and Business Media LLC, Mar. 2022, pp. 4991–5023, doi:10.1007/s00500-022-06903-5.