目录
简介
树是类似于链表的数据结构,和链表的线性结构不同的是,树是具有层次结构的非线性的数据结构。
树是由很多个节点组成的,每个节点可以指向很多个节点。
如果一个树中的每个节点都只有0,1,2个子节点的话,这颗树就被称为二叉树,如果我们对二叉树进行一定的排序。
比如,对于二叉树中的每个节点,如果左子树节点的元素都小于根节点,而右子树的节点的元素都大于根节点,那么这样的树被叫做二叉搜索树(Binary Search Tree)简称BST。
今天我们来探讨一下BST的性质和对BST的基本操作。
BST的基本性质
刚刚我们已经讲过BST的基本特征了,现在我们再来总结一下:
- BST中任意节点的左子树一定要比该节点的值要小
- BST中任意节点的右子树一定要比该节点的值要大
- BST中任意节点的左右子树一定要是一个BST。
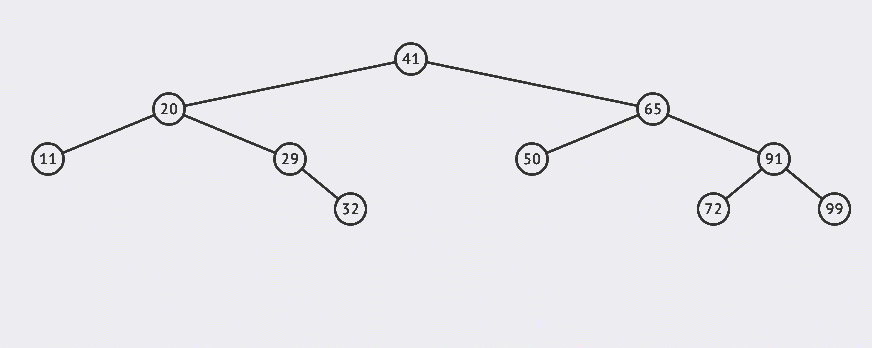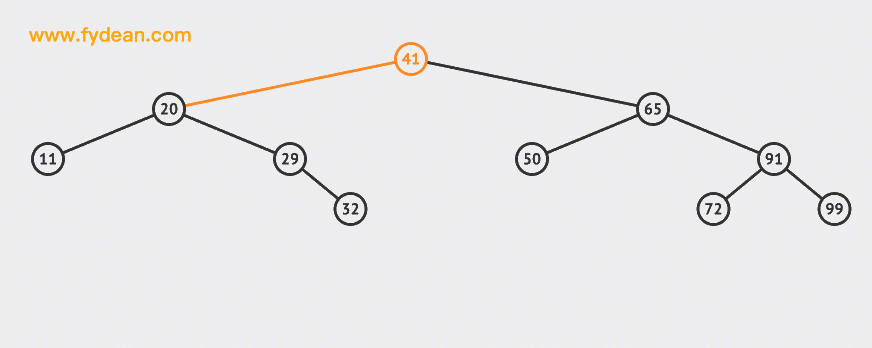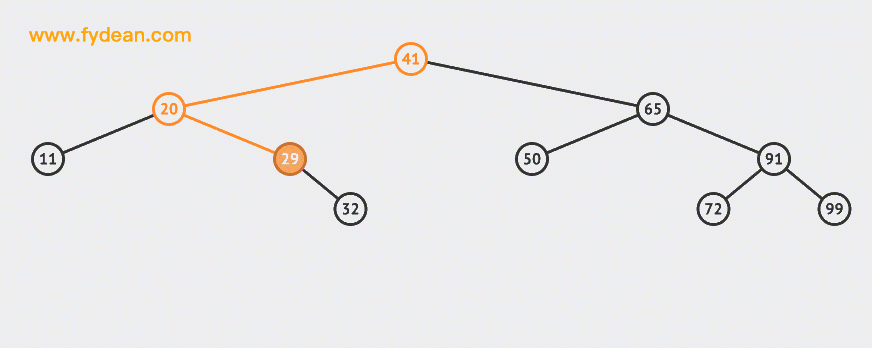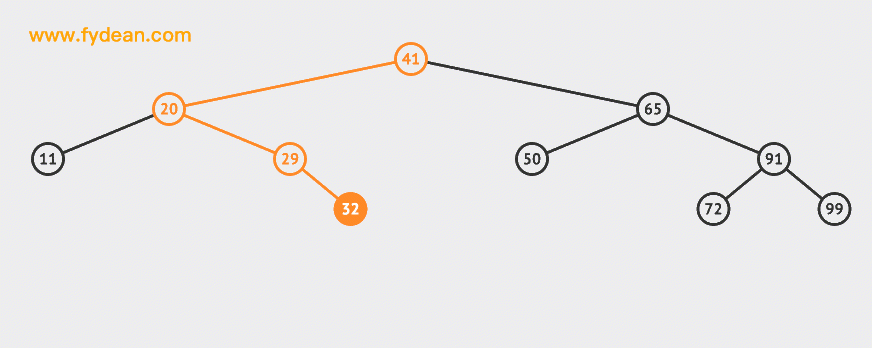
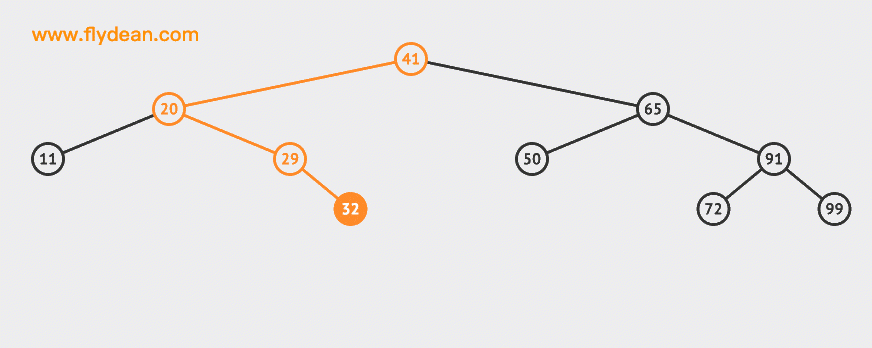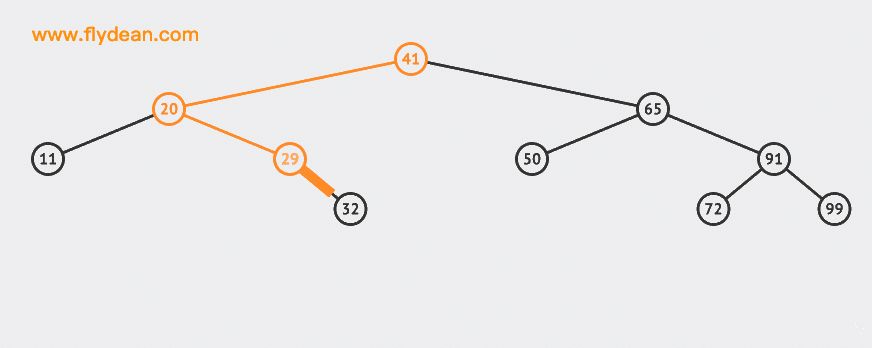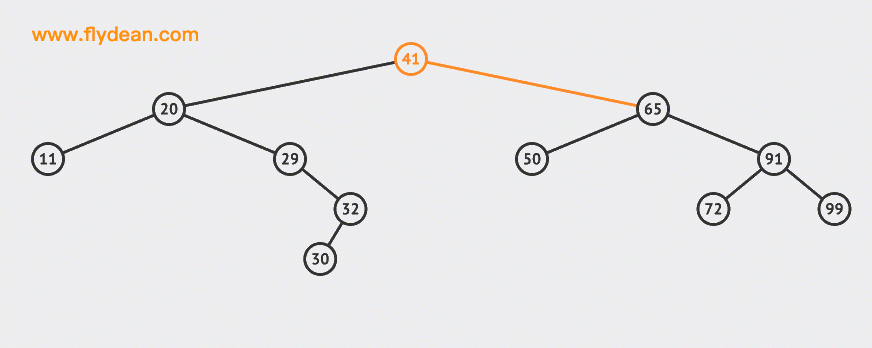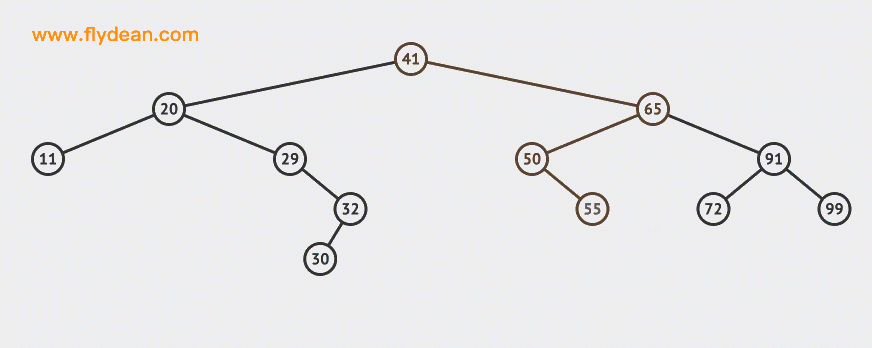
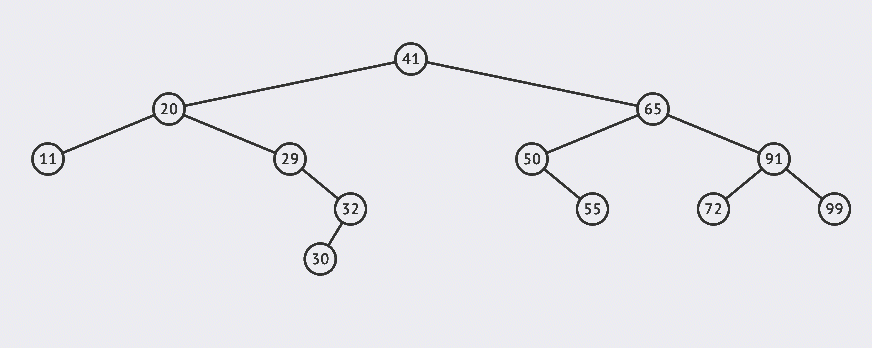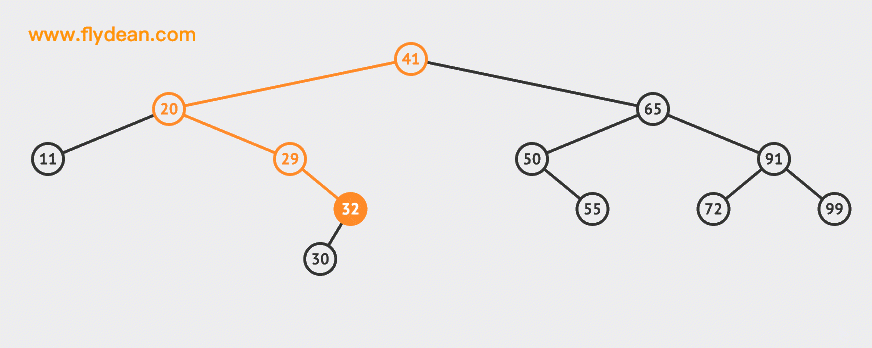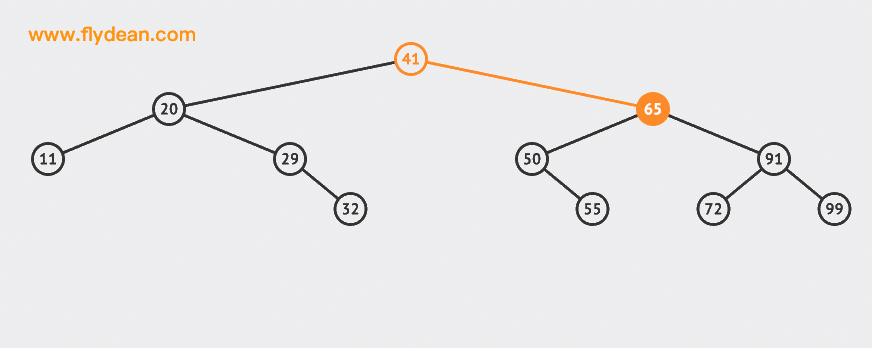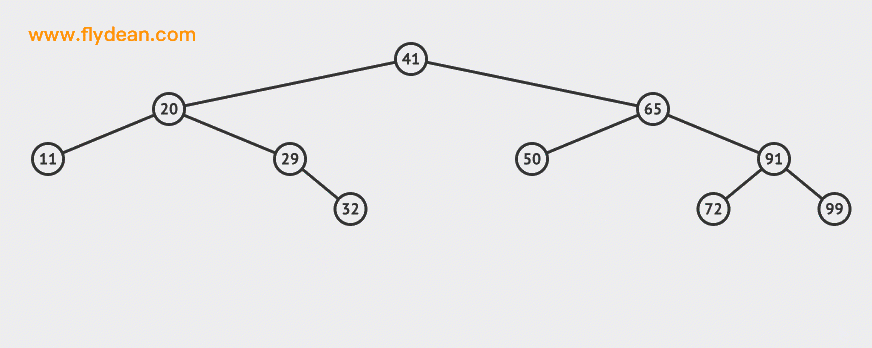
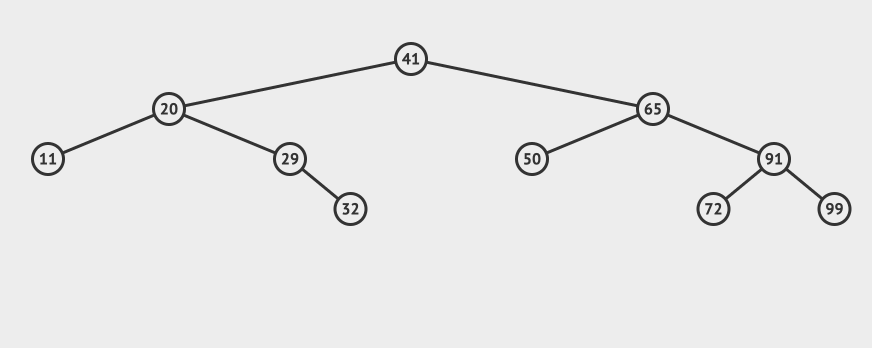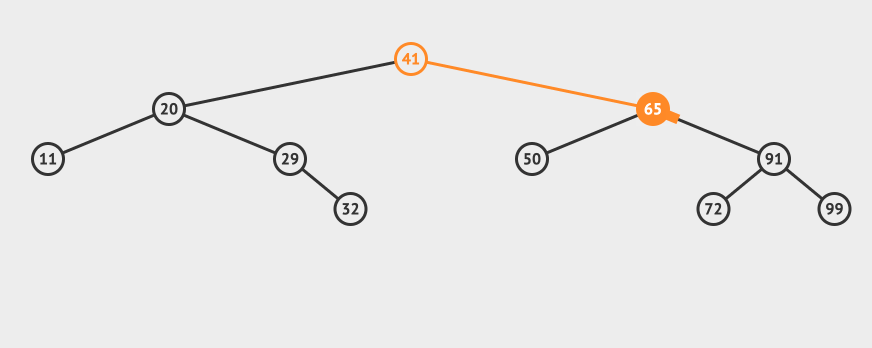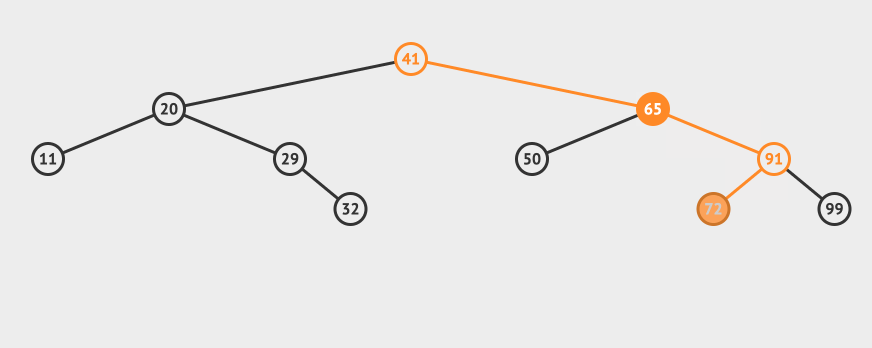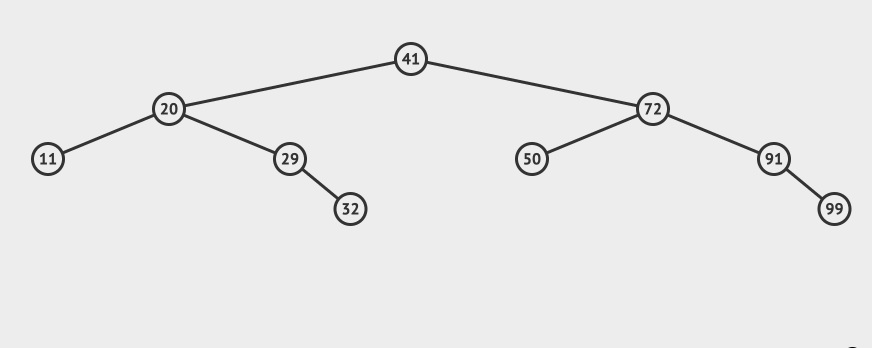
看一张图直观的感受一下BST:
BST的构建
怎么用代码来构建一个BST呢?
首先,BST是由一个一个的节点Node组成的,Node节点除了保存节点的数据之外,还需要指向左右两个子节点,这样我们的BST完全可以由Node连接而成。
另外我们还需要一个root节点来表示BST的根节点。
相应的代码如下:
public class BinarySearchTree { //根节点 Node root; class Node { int data; Node left; Node right; public Node(int data) { this.data = data; left = right = null; } } }
BST的搜索
先看下BST的搜索,如果是上面的BST,我们想搜索32这个节点应该是什么样的步骤呢?
先上图:
搜索的基本步骤是:
- 从根节点41出发,比较根节点和搜索值的大小
- 如果搜索值小于节点值,那么递归搜索左侧树
- 如果搜索值大于节点值,那么递归搜索右侧树
- 如果节点匹配,则直接返回即可。
相应的java代码如下:
//搜索方法,默认从根节点搜索 public Node search(int data){ return search(root,data); } //递归搜索节点 private Node search(Node node, int data) { // 如果节点匹配,则返回节点 if (node==null || node.data==data) return node; // 节点数据大于要搜索的数据,则继续搜索左边节点 if (node.data > data) return search(node.left, data); // 如果节点数据小于要搜素的数据,则继续搜索右边节点 return search(node.right, data); }
BST的插入
搜索讲完了,我们再讲BST的插入。
先看一个动画:
上的例子中,我们向BST中插入两个节点30和55。
插入的逻辑是这样的:
- 从根节点出发,比较节点数据和要插入的数据
- 如果要插入的数据小于节点数据,则递归左子树插入
- 如果要插入的数据大于节点数据,则递归右子树插入
- 如果根节点为空,则插入当前数据作为根节点
相应的java代码如下:
// 插入新节点,从根节点开始插入 public void insert(int data) { root = insert(root, data); } //递归插入新节点 private Node insert(Node node, int data) { //如果节点为空,则创建新的节点 if (node == null) { node = new Node(data); return node; } //节点不为空,则进行比较,从而递归进行左侧插入或者右侧插入 if (data < node.data) node.left = insert(node.left, data); else if (data > node.data) node.right = insert(node.right, data); //返回插入后的节点 return node; }
BST的删除
BST的删除要比插入复杂一点,因为插入总是插入到叶子节点,而删除可能删除的是非叶子节点。
我们先看一个删除叶子节点的例子:
上面的例子中,我们删除了30和55这两个节点。
可以看到,删除叶子节点是相对简单的,找到之后删除即可。
我们再来看一个比较复杂的例子,比如我们要删除65这个节点:
可以看到需要找到65这个节点的右子树中最小的那个,替换掉65这个节点即可(当然也可以找到左子树中最大的那个)。
所以删除逻辑是这样的:
- 从根节点开始,比较要删除节点和根节点的大小
- 如果要删除节点比根节点小,则递归删除左子树
- 如果要删除节点比根节点大,则递归删除右子树
- 如果节点匹配,又有两种情况
- 如果是单边节点,直接返回节点的另外一边
- 如果是双边节点,则先找出右边最小的值,作为根节点,然后将删除最小值过后的右边的节点,作为根节点的右节点
看下代码的实现:
// 删除新节点,从根节点开始删除 void delete(int data) { root = delete(root, data); } //递归删除节点 Node delete(Node node, int data) { //如果节点为空,直接返回 if (node == null) return node; //遍历左右两边的节点 if (data < node.data) node.left = delete(node.left, data); else if (data > root.data) node.right = delete(node.right, data); //如果节点匹配 else { //如果是单边节点,直接返回其下面的节点 if (node.left == null) return node.right; else if (node.right == null) return node.left; //如果是双边节点,则先找出右边最小的值,作为根节点,然后将删除最小值过后的右边的节点,作为根节点的右节点 node.data = minValue(node.right); // 从右边删除最小的节点 node.right = delete(node.right, node.data); } return node; }
这里我们使用递归来实现的删除双边节点,大家可以考虑一下有没有其他的方式来删除呢?
本文的代码地址: