在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合 [1] ,最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。
矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中。 [2] 在物理学中,矩阵于电路学、力学、光学和量子物理中都有应用;计算机科学中,三维动画制作也需要用到矩阵。 矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。对一些应用广泛而形式特殊的矩阵,例如稀疏矩阵和准对角矩阵,有特定的快速运算算法。关于矩阵相关理论的发展和应用,请参考《矩阵理论》。在天体物理、量子力学等领域,也会出现无穷维的矩阵,是矩阵的一种推广。
数值分析的主要分支致力于开发矩阵计算的有效算法,这是一个已持续几个世纪以来的课题,是一个不断扩大的研究领域。 矩阵分解方法简化了理论和实际的计算。 针对特定矩阵结构(如稀疏矩阵和近角矩阵)定制的算法在有限元方法和其他计算中加快了计算。 无限矩阵发生在行星理论和原子理论中。 无限矩阵的一个简单例子是代表一个函数的泰勒级数的导数算子的矩阵 [3]
二维数组的打印。
package 案例回顾47; import java.util.Scanner; /** * * @author MZFAITHDREAM * */ public class 二维数组的打印 { int [] []arrays=null; private void init() { Scanner scanner=new Scanner(System.in); int n=scanner.nextInt(); scanner.close(); arrays=new int [n][n]; int num=0; for (int i = 0; i < arrays.length; i++) { for (int j = 0; j < arrays.length; j++) { arrays[i][j]=++num; System.out.print(arrays[i][j]+"\t"); } System.out.println(); } } public static void main(String[] args) { new 二维数组的打印().init(); } }
矩阵顺时针針打印。
package 第四章矩阵知识讲解; import java.util.Scanner; /** * 1.随机给定一个二维数组,要求按照顺时针打印数字 * @author lenovo-1 * * 顺时针針打印 * */ public class Demo1 { int[][] nums=null; private void init() { System.out.println("输入二维数组的阶数:"); Scanner scanner=new Scanner(System.in); int n=scanner.nextInt(); scanner.close(); nums=new int[n][n]; int num=0; for (int i = 0; i < nums.length; i++) { for (int j = 0; j < nums[i].length; j++) { nums[i][j]=++num; System.out.print(nums[i][j]+"\t"); } System.out.println(); } print(); } private void print() { System.out.println("结果为:"); //确定好当前二维数组的范围 int x1=0,y1=0,x2=nums.length-1,y2=nums[0].length-1; //控制移动的圈数 while (x1<=x2&&y1<=y2) { //定义一个移动点坐标 int x=x1,y=y1; //向右移动,x不动,y在增加,但不能超出y2的边界 while (y<=y2) { System.out.print(nums[x][y++]+"\t"); } //将移动点的纵坐标赋值为y2 y=y2; //x=x+1; x++; //向下移动 while (x<=x2) { System.out.print(nums[x++][y]+"\t"); } x=x2; y--; //向左移动 while (y>=y1) { System.out.print(nums[x][y--]+"\t"); } y=y1; x--; //向上移动 while (x>x1) { System.out.print(nums[x--][y]+"\t"); } //让范围缩小 x1++;y1++;x2--;y2--; } } public static void main(String[] args) { new Demo1().init(); } }
矩阵逆時針打印
package 第四章矩阵知识讲解; import java.util.Scanner; /** * 逆時針 * @author lenovo * */ public class Demo2 { int[][] nums=null; private void init() { // TODO Auto-generated method stub System.out.println("输入二维数组的阶数:"); Scanner scanner=new Scanner(System.in); int n=scanner.nextInt(); scanner.close(); nums=new int[n][n]; int num=0; for (int i = 0; i < nums.length; i++) { for (int j = 0; j < nums[i].length; j++) { nums[i][j]=++num; System.out.print(nums[i][j]+"\t"); } System.out.println(); } print(); } private void print() { System.out.println("结果:"); //確定二維數組的范围 int x1=0,y1=0,x2=nums.length-1,y2=nums[0].length-1; while (x1<=x2&&y1<=y2) { //定义一个移动点坐标 int x=x1,y=y1; //向下移动,在同一列移动,x在增加,y不变 while (x<=x2) { System.out.print(nums[x++][y]+"\t"); } x=x2; y++; //向右走,同一行,x不变,y在增加 while (y<=y2) { System.out.print(nums[x][y++]+"\t"); } y=y2; x--; //向上走,同一列,y不变,x在递减 while (x>=x1) { System.out.print(nums[x--][y]+"\t"); } x=x1; y--; //向左走,同一行,x不变,y在递减 while (y>y1) { System.out.print(nums[x][y--]+"\t"); } x1++;y1++;x2--;y2--; } } public static void main(String[] args) { // TODO Auto-generated method stub new Demo2().init(); } }
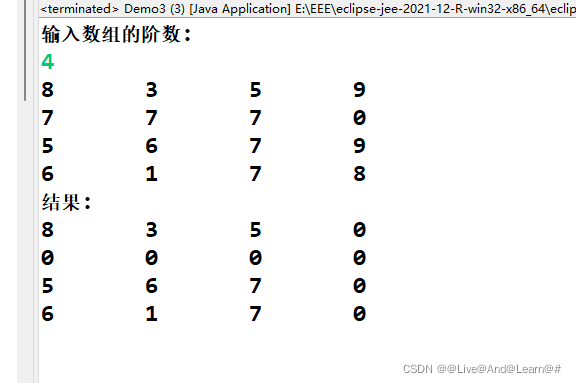
矩阵中一个为0XY全部为0.
package 第四章矩阵知识讲解; import java.util.Random; import java.util.Scanner; public class Demo3 { int[][] nums=null; private void init() { System.out.println("输入数组的阶数:"); Scanner scanner=new Scanner(System.in); int n=scanner.nextInt(); scanner.close(); nums=new int[n][n]; for (int i = 0; i < nums.length; i++) { for (int j = 0; j < nums[i].length; j++) { //随机性产生0 nums[i][j]=Math.random()>0.1?new Random().nextInt(9)+1:0; System.out.print(nums[i][j]+"\t"); } System.out.println(); } print(); } private void print() { System.out.println("结果:"); //创建两个一维数组,分别用于记录为0的横纵坐标 int[] row=new int[nums.length]; int[] col=new int[nums[0].length]; //循环遍历所有的点 for (int i = 0; i < nums.length; i++) { for (int j = 0; j < nums[i].length; j++) { if (nums[i][j]==0) { row[i]=1; col[j]=1; } } } //判断两个一维数组中记录的下标的位置所在的整行和整列清零 for (int i = 0; i < nums.length; i++) { for (int j = 0; j < nums[i].length; j++) { if (row[i]==1||col[j]==1) { nums[i][j]=0; } System.out.print(nums[i][j]+"\t"); } System.out.println(); } } public static void main(String[] args) { new Demo3().init(); } }