机器学习:在梯度下降法中为什么梯度的方向是变化最快的方向
基础概念
一阶导数
在一阶函数中,一阶导数表示函数值与自变量的变化关系,我们把函数从一个点到另一个点变化的函数值与变化的自变量的比值称为函数这两点之间自变量方向的变化率,可以用$\frac{\Delta y}{\Delta x}$表示,当自变量x的变化趋近于0的时候,他们的比值叫做函数的导数,也可以叫做在函数某点沿着自变量变化的斜率。用$tan\Theta$表示。 $$\begin{aligned}f'\left( x\right) =\lim _{\Delta x\rightarrow 0}\dfrac{f\left( x+\Delta x\right) -f\left( x\right) }{\Delta \chi }\end{aligned}$$
$$\begin{aligned}f'\left( x\right) =\lim _{\Delta x\rightarrow 0}\dfrac{f\left( x+\Delta x\right) -f\left( x\right) }{\Delta \chi }\end{aligned}$$
偏导数
接下来,我们把自变量的格局打开(升维),从一元函数上升到多元函数,$z = f(x,y)$,现在我们对一个自变量求导,它反映了多元函数与其中一个自变量的变化关系,也叫做偏导数,他表示函数值在这个点$\Delta x$方向上的变化率。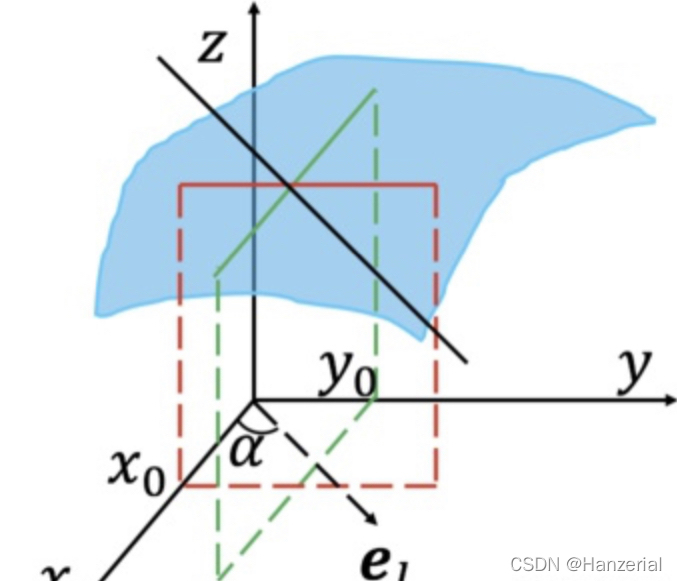
方向导数
看到这里,我们可能会有一个疑问,求导的那个点的方向一定是沿着坐标轴的吗?如图所示,他可以是任意方向。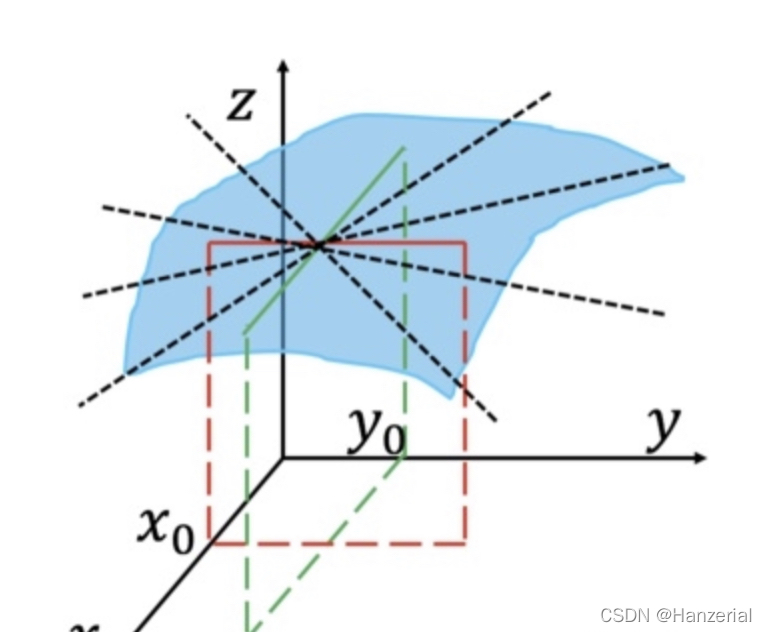
假设有一个向量l,步长为t,角度为$\Theta$我们要求得函数在l方向上的方向导数,有下图可知,向量l在x轴方向上的改变量为$t sin\Theta$,y轴的改变量为$t cos\Theta$,所以公式可表示为:$$f\left( x\right) ^{'}=\lim _{t\rightarrow 0}\dfrac{f\left( x+t\sin \theta ,y+t\cos \theta \right) -f\left( x,y\right) }{t}$$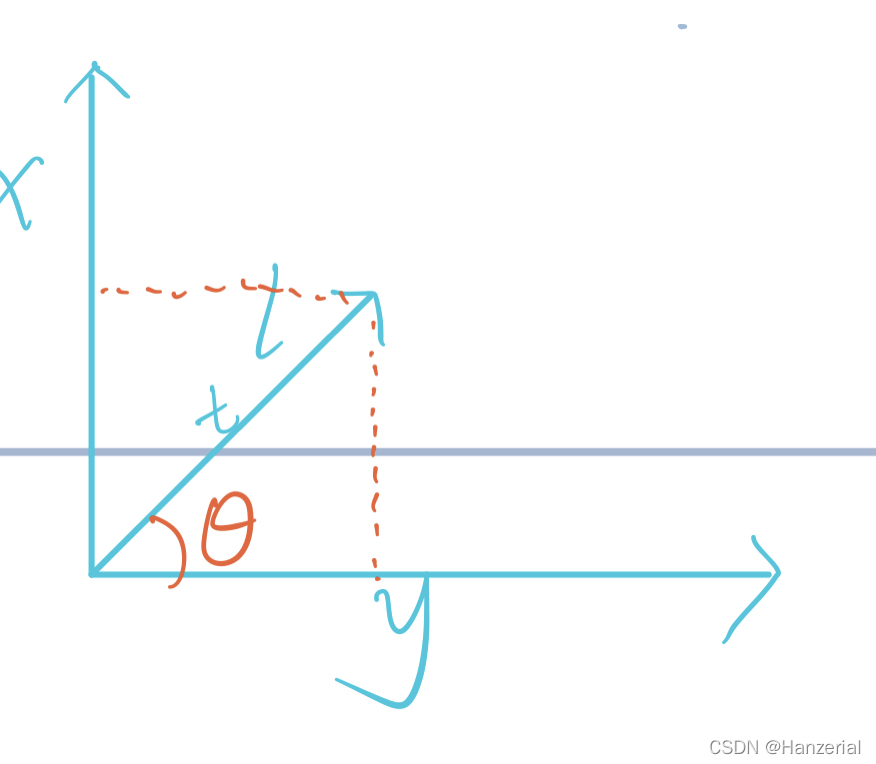
梯度
梯度是导数对多远函数的推广,他是对各个自变量偏导数形成的向量,其作用相当于一元函数的导数,之前我们介绍了导数与偏导数,偏导数是一个标量。某个点的梯度代表某个点在多元函数在这点变化方向。
$$\nabla f\left( x\right) =\begin{pmatrix} \dfrac{\partial f}{\partial x_{1}} & \ldots & \dfrac{\partial f}{\partial x_{n}} \end{pmatrix}^{T}$$
验证
接下来到了最激动人心的时刻,我们来验证为什么函数在这个点的梯度的方向是函数在这个点梯度增加最快的方向。设在某一点在向量l方向的方向导数:
$$f\left( x\right) ^{'}=\lim _{t\rightarrow 0}\dfrac{f\left( x+t\sin \theta ,y+t\cos \theta \right) -f\left( x,y\right) }{t}$$
通过链式法则,化简如下:
$$\begin{aligned}=\dfrac{\partial f}{\partial x}\cdot \dfrac{\partial x}{\partial t}+\dfrac{\partial f}{\partial y}\dfrac{\partial y}{\partial t}\\ =\sin \theta \dfrac{\partial f }{\partial x}+\cos \theta \dfrac{\partial f}{\partial y}\end{aligned}$$

