AI 助理
备案控制台
开发者社区 云计算 文章 正文

数据结构之AVL

2022-06-07 307
版权
版权声明：
本文内容由阿里云实名注册用户自发贡献，版权归原作者所有，阿里云开发者社区不拥有其著作权，亦不承担相应法律责任。具体规则请查看《 阿里云开发者社区用户服务协议》和 《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容，填写 侵权投诉表单进行举报，一经查实，本社区将立刻删除涉嫌侵权内容。
简介： AVL

AVL

平衡二叉树

平衡二叉查找树：简称平衡二叉树。由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962 年提出的高度平衡的二叉树，根据科学家的英文名也称为 AVL 树。它具有如下几个性质：


  1. 可以是空树。
  2. 假如不是空树，任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过 1。


二叉搜索树一定程度上可以提高搜索效率，但是当原序列有序时，例如序列 {1，2，3，4，5，6}，构造二叉搜索树。依据此序列构造的二叉搜索树为右斜树，同时二叉树退化成单链表，搜索效率降低为 O(n)。

1654601973006.png

在此二叉搜索树中查找元素 6 需要查找 6 次。


二叉搜索树的查找效率取决于树的高度，因此保持树的高度最小，即可保证树的查找效率。同样的序列 A，将其改为图中的方式存储，查找元素 6 时只需比较 3 次，查找效率提升一倍。

1654602037660.png

可以看出当节点数目一定，保持树的左右两端保持平衡，树的查找效率最高。


这种左右子树的高度相差不超过 1 的树为平衡二叉树。


平衡因子

某节点的左子树与右子树的高度(深度)差即为该节点的平衡因子（BF：Balance Factor）。


节点为2的深度为1，由于没有子节点所有平衡因子是0，节点为4的深度为2，平衡因子是左孩子减去右孩子所以是1-0 = 1 ，平衡因子为1。依次类推，当有节点大于1的时候就说明不是平衡二叉树。

1654602230796.png

public class AVLTree<K extends Comparable<K>, V> {
    private class Node{
        public K key;
        public V value;
        public Node left, right;
        public int height;
        public Node(K key, V value){
            this.key = key;
            this.value = value;
            left = null;
            right = null;
            height = 1;
        }
    }
    private Node root;
    private int size;
    public AVLTree(){
        root = null;
        size = 0;
    }
    public int getSize(){
        return size;
    }
    public boolean isEmpty(){
        return size == 0;
    }
    // 获得节点node的高度
    private int getHeight(Node node){
        if(node == null) {
            return 0;
        }
        return node.height;
    }
    // 获得节点node的平衡因子
    private int getBalanceFactor(Node node){
        if(node == null) {
            return 0;
        }
        return getHeight(node.left) - getHeight(node.right);
    }
    // 向二分搜索树中添加新的元素(key, value)
    public void add(K key, V value){
        root = add(root, key, value);
    }
    // 向以node为根的二分搜索树中插入元素(key, value)，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, K key, V value){
        if(node == null){
            size ++;
            return new Node(key, value);
        }
        if(key.compareTo(node.key) < 0) {
            node.left = add(node.left, key, value);
        } else if(key.compareTo(node.key) > 0) {
            node.right = add(node.right, key, value);
        } else // key.compareTo(node.key) == 0
        {
            node.value = value;
        }
        // 更新height
        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
        // 计算平衡因子
        int balanceFactor = getBalanceFactor(node);
        if(Math.abs(balanceFactor) > 1) {
            System.out.println("unbalanced : " + balanceFactor);
        }
        return node;
    }
    // 返回以node为根节点的二分搜索树中，key所在的节点
    private Node getNode(Node node, K key){
        if(node == null) {
            return null;
        }
        if(key.equals(node.key)) {
            return node;
        } else if(key.compareTo(node.key) < 0) {
            return getNode(node.left, key);
        } else // if(key.compareTo(node.key) > 0)
        {
            return getNode(node.right, key);
        }
    }
    public boolean contains(K key){
        return getNode(root, key) != null;
    }
    public V get(K key){
        Node node = getNode(root, key);
        return node == null ? null : node.value;
    }
    public void set(K key, V newValue){
        Node node = getNode(root, key);
        if(node == null) {
            throw new IllegalArgumentException(key + " doesn't exist!");
        }
        node.value = newValue;
    }
    // 返回以node为根的二分搜索树的最小值所在的节点
    private Node minimum(Node node){
        if(node.left == null) {
            return node;
        }
        return minimum(node.left);
    }
    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMin(Node node){
        if(node.left == null){
            Node rightNode = node.right;
            node.right = null;
            size --;
            return rightNode;
        }
        node.left = removeMin(node.left);
        return node;
    }
    // 从二分搜索树中删除键为key的节点
    public V remove(K key){
        Node node = getNode(root, key);
        if(node != null){
            root = remove(root, key);
            return node.value;
        }
        return null;
    }
    private Node remove(Node node, K key){
        if( node == null ) {
            return null;
        }
        if( key.compareTo(node.key) < 0 ){
            node.left = remove(node.left , key);
            return node;
        }
        else if(key.compareTo(node.key) > 0 ){
            node.right = remove(node.right, key);
            return node;
        }
        else{   // key.compareTo(node.key) == 0
            // 待删除节点左子树为空的情况
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size --;
                return rightNode;
            }
            // 待删除节点右子树为空的情况
            if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size --;
                return leftNode;
            }
            // 待删除节点左右子树均不为空的情况
            // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
            // 用这个节点顶替待删除节点的位置
            Node successor = minimum(node.right);
            successor.right = removeMin(node.right);
            successor.left = node.left;
            node.left = node.right = null;
            return successor;
        }
    }
}

二分搜索树性质和平衡性

判断该树是否是一颗二分搜索树


所谓的二分搜索树，就是任意一个节点满足，大于左孩子，小于右孩子。所以二分搜索树满足这样的一个性质：中序遍历之后的二叉树是顺序的。所以我们这里实现的思路是，改写二叉树的非递归版本的，来校验当前值和前一个值的大小关系。

//判断该二叉树是否是一颗二分搜索树
    public boolean isBST() {
        List<K> keys = new ArrayList<>();
        inOrder(root, keys);
        for (int i = 0; i < keys.size(); i++) {
            if (keys.get(i - 1).compareTo(keys.get(i)) > 0) {
                return false;
            }
        }
        return true;
    }
    private void inOrder(Node node, List<K> keys) {
        if (node == null) {
            return;
        }
        inOrder(node.left, keys);
        keys.add(node.key);
        inOrder(node.right, keys);
    }

判断该树是否是一颗平衡二叉树


  • 1.判断以根结点的树是否为平衡二叉树。求出左右子树的高度，判断它们的高度差是否超过了1。
  • 2.递归判断根的左子树是否为平衡二叉树
  • 3.递归判断根的右子树是否为平衡二叉树
    注意：空树也是平衡二叉树

   

//判断该二叉树是否是一颗平衡二叉树
    public boolean isBalanced() {
        return isBalanced(root);
    }
    //判断以Node为根的二叉树是否是一颗平衡二叉树，递归算法
    private boolean isBalanced(Node node) {
        if (node == null) {
            return true;
        }
        int balanceFactor = getBalanceFactor(node);
        if (Math.abs(balanceFactor) > 1) {
            return false;
        }
        return isBalanced(node.left) && isBalanced(node.right);
    }

旋转操作的基本原理


我们在插入数据的时候可能会打破平衡性，所以我们需要沿着节点向上维护平衡性。


在什么时候维护平衡？


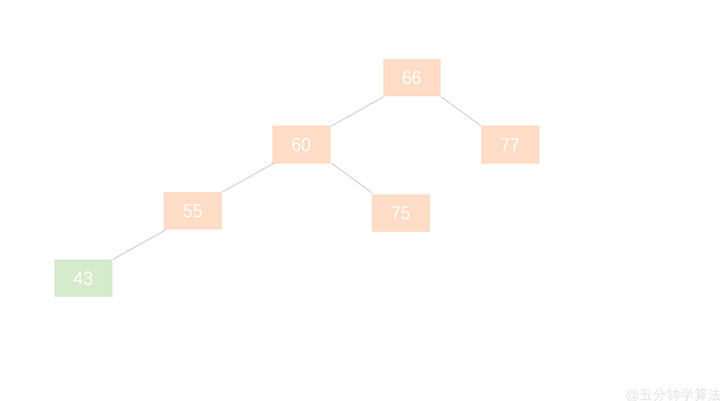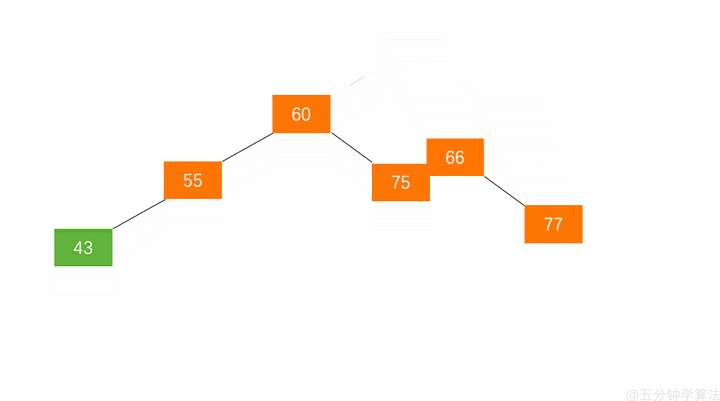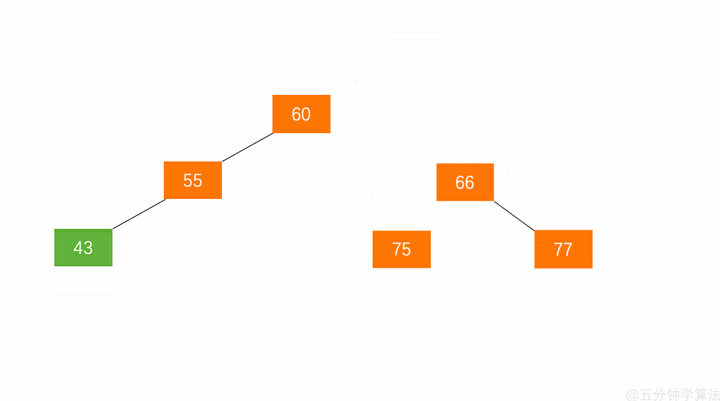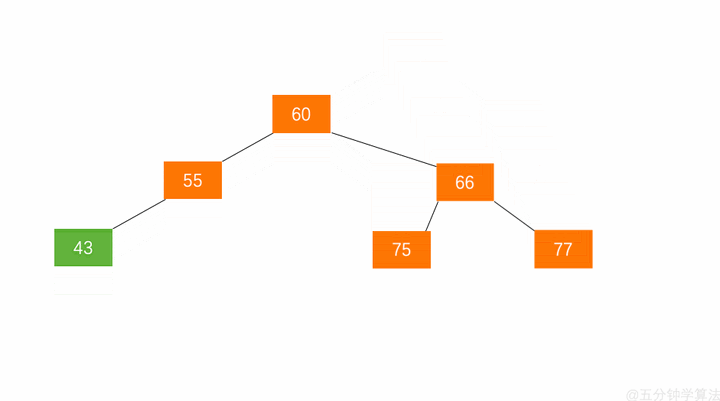
在一开始，我们添加一个节点12，平衡因子是0。

1654602466884.png

然后添加一个节点8，这时候平衡因子是0，而12的平衡因子是1。

1654602507994.png

然后添加一个节点5，这时候平衡因子是0，而8的平衡因子是1，12的平衡因子就变为了2。


这时候就不再是平衡二叉树。

1654602570291.png

右旋（LL）

  1. 根节点（Y）的左孩子代表根节点
  2. （X）节点的右子树变为（Y）的左子树
  3. 将此节点（Y）变为（X）根节点的右子树


代码逻辑为：

x.right = y
y.left = T3

1654602699741.png

动图引用于此

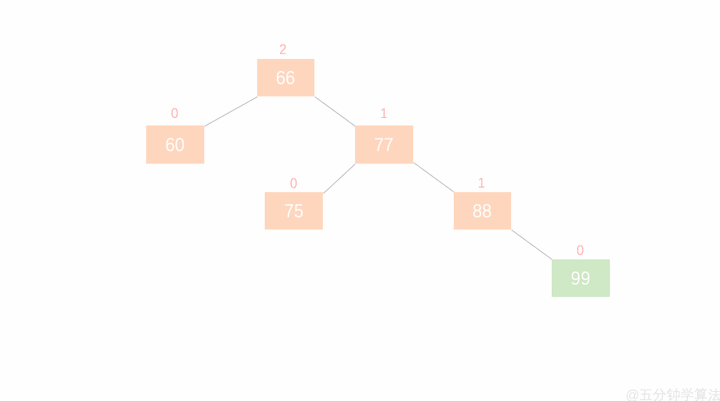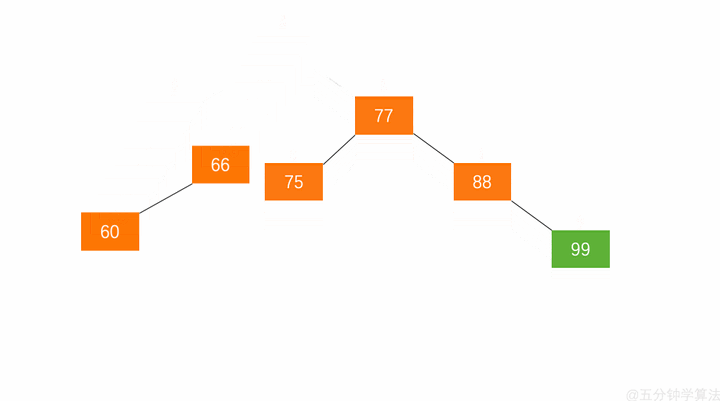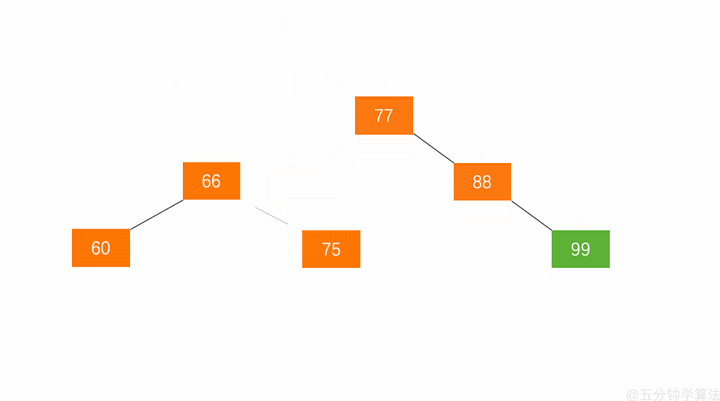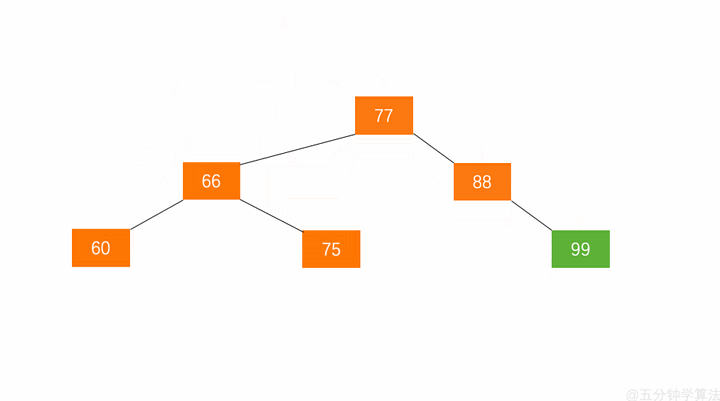
具体动画演示如下：

v2-05246384c1c16537ca6176983bdb2627_b.gif

当旋转之后，我们这棵树依旧保持二分搜索树和平衡二叉树的性质。

  

// 向以node为根的二分搜索树中插入元素(key, value)，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, K key, V value) {
        if (node == null) {
            size++;
            return new Node(key, value);
        }
        if (key.compareTo(node.key) < 0) {
            node.left = add(node.left, key, value);
        } else if (key.compareTo(node.key) > 0) {
            node.right = add(node.right, key, value);
        } else // key.compareTo(node.key) == 0
        {
            node.value = value;
        }
        // 更新height
        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
        // 计算平衡因子
        int balanceFactor = getBalanceFactor(node);
        if (Math.abs(balanceFactor) > 1) {
            System.out.println("unbalanced : " + balanceFactor);
        }
        //平衡维护
        if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
            return rightRotate(node);
        }
        return node;
    }
    // 对节点y进行向右旋转操作，返回旋转后新的根节点x
    //        y                              x
    //       / \                           /   \
    //      x   T4     向右旋转 (y)        z     y
    //     / \       - - - - - - - ->    / \   / \
    //    z   T3                       T1  T2 T3 T4
    //   / \
    // T1   T2
    private Node rightRotate(Node y) {
        Node x = y.left;
        Node t3 = x.right;
        x.right = y;
        y.left = t3;
        //更新x和y的高度
        y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
        x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
        return x;
    }

左旋（RR）

  1. 根节点（Y）的右孩子替代根节点位置
  2. （X）的左子树变为（Y）的右子树
  3. （Y）本身变为（X）的左子树


代码逻辑为：

x.left = y;
y.right = t3;

1654602870450(1).png

动图如下：

v2-db1cdb0da952a71f9b6d64b2608467eb_b.gif

LR和RL

LR的情况


如下图这样的情况，我们插入一个节点10，这个时候10和12都比8大，我们不管是使用LL还是RR都无法达到效果。

1654602925696.png

我们首先可以对x节点进行左旋，得到如下图所示，这样我就会发现当前树结构已经变成了LL的情况，我们进行右旋即可。

1654602942306.png

动图演示：

1654603063617.png

RL的情况

RL和LR其实是对称的关系。

我们首先将x进行右旋，然后转换为RR的情况，再进行左旋即可。

1654603110701.png

// 向以node为根的二分搜索树中插入元素(key, value)，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, K key, V value) {
        if (node == null) {
            size++;
            return new Node(key, value);
        }
        if (key.compareTo(node.key) < 0) {
            node.left = add(node.left, key, value);
        } else if (key.compareTo(node.key) > 0) {
            node.right = add(node.right, key, value);
        } else // key.compareTo(node.key) == 0
        {
            node.value = value;
        }
        // 更新height
        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
        // 计算平衡因子
        int balanceFactor = getBalanceFactor(node);
        if (Math.abs(balanceFactor) > 1) {
            System.out.println("unbalanced : " + balanceFactor);
        }
        //平衡维护  LL
        if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
            return rightRotate(node);
        }
        //平衡维护  RR
        if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
            return leftRotate(node);
        }
        //平衡维护  LR
        if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }
        //平衡维护  RL
        if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }
        return node;
    }

从AVL中删除元素

删除和添加代码类似，具体也是删除元素后进行平衡维护。


// 从二分搜索树中删除键为key的节点
    public V remove(K key) {
        Node node = getNode(root, key);
        if (node != null) {
            root = remove(root, key);
            return node.value;
        }
        return null;
    }
    private Node remove(Node node, K key) {
        if (node == null) {
            return null;
        }
        Node retNode;
        if (key.compareTo(node.key) < 0) {
            node.left = remove(node.left, key);
            retNode = node;
        } else if (key.compareTo(node.key) > 0) {
            node.right = remove(node.right, key);
            retNode = node;
        } else {   // key.compareTo(node.key) == 0
            // 待删除节点左子树为空的情况
            if (node.left == null) {
                Node rightNode = node.right;
                node.right = null;
                size--;
                retNode = rightNode;
            }
            // 待删除节点右子树为空的情况
            else if (node.right == null) {
                Node leftNode = node.left;
                node.left = null;
                size--;
                retNode = leftNode;
            } else {
                // 待删除节点左右子树均不为空的情况
                // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
                // 用这个节点顶替待删除节点的位置
                Node successor = minimum(node.right);
                successor.right = remove(node.right, successor.key);
                successor.left = node.left;
                node.left = node.right = null;
                retNode = successor;
            }
        }
        if(retNode == null){
            return null;
        }
        // 更新height
        retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
        // 计算平衡因子
        int balanceFactor = getBalanceFactor(retNode);
        if (Math.abs(balanceFactor) > 1) {
            System.out.println("unbalanced : " + balanceFactor);
        }
        //平衡维护  LL
        if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
            return rightRotate(retNode);
        }
        //平衡维护  RR
        if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
            return leftRotate(retNode);
        }
        //平衡维护  LR
        if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
            node.left = leftRotate(retNode.left);
            return rightRotate(retNode);
        }
        //平衡维护  RL
        if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
            node.right = rightRotate(retNode.right);
            return leftRotate(retNode);
        }
        return retNode;
    }
文章标签：
存储
关键词：
数据结构avl
jackcode0323
目录
相关文章
Echo_Wish
|
8月前
|
编译器 数据库 索引
Python高级数据结构——AVL树
Python高级数据结构——AVL树
Echo_Wish
141 2
慕斯(˘▽˘)っ
|
8月前
|
C++
【数据结构】—AVL树（C++实现）
【数据结构】—AVL树（C++实现）
慕斯(˘▽˘)っ
88 0
java冯坚持
|
3月前
|
存储 算法 数据管理
数据结构与算法学习二零：二叉排序树（BST）、平衡二叉树（AVL）
这篇文章通过需求分析、代码实现和测试验证，详细介绍了二叉排序树的创建、遍历和删除操作，以及二叉平衡树（AVL）的自平衡特性和单旋转操作，旨在提高树结构在数据管理中的效率和性能。
java冯坚持
65 0
数据结构与算法学习二零：二叉排序树（BST）、平衡二叉树（AVL）
是店小二呀
|
3月前
【高阶数据结构】二叉树进阶探秘：AVL树的平衡机制与实现详解（三）
【高阶数据结构】二叉树进阶探秘：AVL树的平衡机制与实现详解
是店小二呀
37 1
是店小二呀
|
3月前
【高阶数据结构】二叉树进阶探秘：AVL树的平衡机制与实现详解（二）
【高阶数据结构】二叉树进阶探秘：AVL树的平衡机制与实现详解
是店小二呀
60 1
是店小二呀
|
3月前
|
存储
【高阶数据结构】二叉树进阶探秘：AVL树的平衡机制与实现详解（一）
【高阶数据结构】二叉树进阶探秘：AVL树的平衡机制与实现详解
是店小二呀
63 1
大柏怎么被偷了
|
5月前
|
C++ 容器
【数据结构】AVL树
【数据结构】AVL树
大柏怎么被偷了
53 0
小蜗牛~向前冲
|
8月前
[数据结构]-AVL树
[数据结构]-AVL树
小蜗牛~向前冲
54 4
[数据结构]-AVL树
东洛的克莱斯韦克
|
6月前
|
存储
【数据结构】AVL树——平衡二叉搜索树
【数据结构】AVL树——平衡二叉搜索树
东洛的克莱斯韦克
42 0
sumith
|
7月前
数据结构篇：旋转操作在AVL树中的实现过程
数据结构篇：旋转操作在AVL树中的实现过程
sumith
50 0

热门文章

最新文章

  • 1
    Python编程数据结构的深入理解
  • 2
    掌握Pandas核心数据结构：Series与DataFrame的四种创建方式
  • 3
    K-means聚类算法是机器学习中常用的一种聚类方法，通过将数据集划分为K个簇来简化数据结构
  • 4
    Python 中的数据结构与其他编程语言数据结构的区别
  • 5
    C语言因高效灵活被广泛应用于软件开发。本文探讨了优化C语言程序性能的策略，涵盖算法优化、代码结构优化、内存管理优化、编译器优化、数据结构优化、并行计算优化及性能测试与分析七个方面
  • 6
    Python 中的数据结构和算法优化策略
  • 7
    Python 中数据结构和算法的关系
  • 8
    在C语言中，数据结构是构建高效程序的基石。本文探讨了数组、链表、栈、队列、树和图等常见数据结构的特点、应用及实现方式
  • 9
    探索局域网电脑监控软件：Python算法与数据结构的巧妙结合
  • 10
    Pandas数据结构：Series与DataFrame
  • 1
    【Python进阶（七）】——Series数据结构
    191
  • 2
    Redis数据结构精讲：选择与应用实战指南
    1337
  • 3
    深入浅出数据结构之布隆过滤器
    76
  • 4
    数据结构/C++：位图 & 布隆过滤器
    49
  • 5
    数据结构/C++：哈希表
    87
  • 6
    数据结构/C++：红黑树
    47
  • 7
    数据结构/C++：AVL树
    50
  • 8
    栈的基本应用
    74
  • 9
    栈与队列理解
    52
  • 10
    数据结构/C++：二叉搜索树
    55

    • 相关课程

    更多
  • Go语言核心编程 - 数据结构和算法

    • 相关电子书

    更多
  • 如何使用Tair增强数据结构构建丰富在线实时场景
  • Apache Flink 流式应用中状态的数据结构定义升级
  • 低代码开发师（初级）实战教程
    • 下一篇
    DataWorks智能交互式数据开发与分析之旅