
版权声明:本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单进行举报,一经查实,本社区将立刻删除涉嫌侵权内容。
当问题规模即要处理的数据增⻓时,基本操作要重复执⾏的次数必定也会增⻓,那么我们关⼼地是这个执⾏次数以什么 样的数量级增⻓。
我们⽤⼤O表示法表示⼀下常⻅的时间复杂度量级:
常数阶O(1) 线性阶O(n) 对数阶O(logn) 线性对数阶O(nlogn) 平⽅阶O(n²)
当然还有指数阶和阶乘阶这种⾮常极端的复杂度量级,我们就不讨论了。
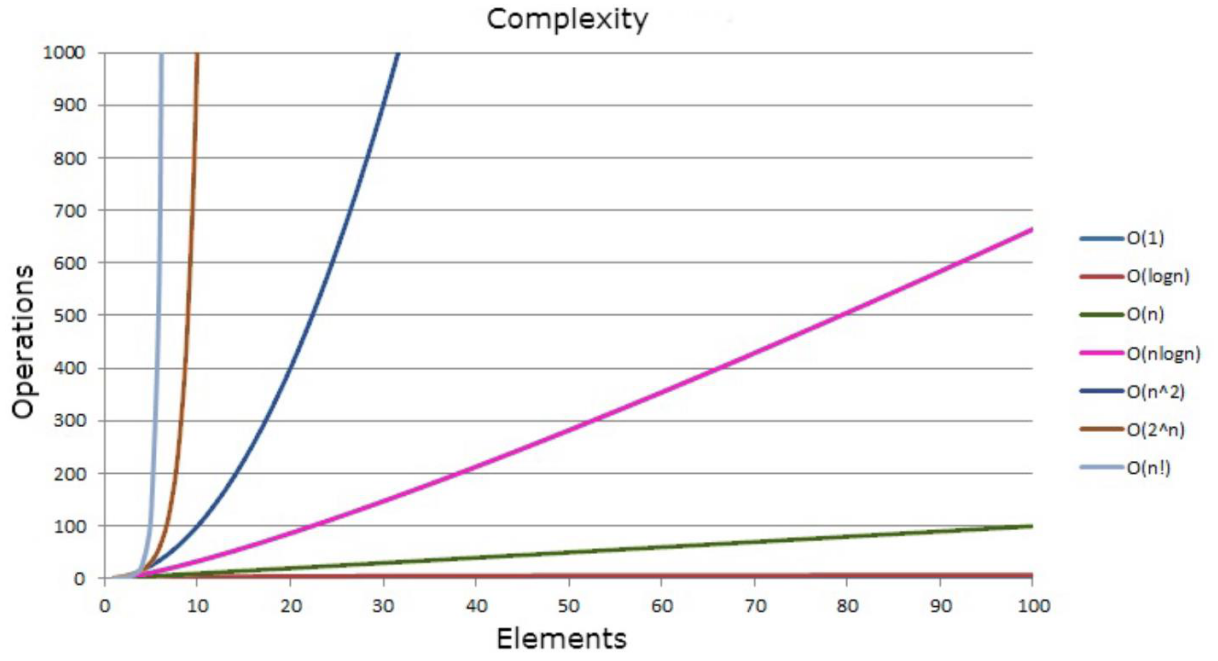
传说中的常数阶的复杂度,这种复杂度⽆论数据规模n如何增⻓,计算时间是不变的。
举⼀个简单的例⼦:
const increment = n => n++
不管n如何增⻓,都不会影响到这个函数的计算时间,因此这个代码的时间复杂度都是O(1)。
线性复杂度,随着数据规模n的增⻓,计算时间也会随着n线性增⻓。
典型的O(n)的例⼦就是线性查找。
const linearSearch = (arr, target) => {
for (let i = 0; i < arr.length; i++) {
if (arr[i] === target) {
return i
}
}
return -1
}
线性查找的时间消化与输⼊的数组数量n成⼀个线性⽐例,随着n规模的增⼤,时间也会线性增⻓。
对数复杂度,随着问题规模n的增⻓,计算时间也会随着n对数级增⻓。
典型的例⼦是⼆分查找法。
functions binarySearch(arr, target) {
let max = arr.length - 1
let min = 0
while (min <= max) {
let mid = Math.floor((max + min) / 2)
if (target < arr[mid]) {
max = mid - 1
} else if (target > arr[mid]) {
min = mid + 1
} else {
return mid
}
}
return -1
}
在⼆分查找法的代码中,通过while循环,成 2 倍数的缩减搜索范围,也就是说需要经过 log2^n 次即可跳出循环。
事实上在实际项⽬中, O(logn) 是⼀个⾮常好的时间复杂度,⽐如当 n=100 的数据规模时,⼆分查找只需要7次,线性查找需要100次,这对于计算机⽽⾔差距不⼤,但是当有10亿的数据规模的时候,⼆分查找依然只需要30次,⽽线性查找需要惊⼈的10亿次, O(logn) 时间复杂度的算法随着数据规模的增⼤,它的优势就越明显。
线性对数复杂度,随着数据规模n的增⻓,计算时间也会随着n呈线性对数级增⻓。
这其中典型代表就是归并排序,我们会在对应⼩节详细分析它的复杂度。
const mergeSort = array => {
const len = array.length
if (len < 2) {
return len
}
const mid = Math.floor(len / 2)
const first = array.slice(0, mid)
const last = array.slice(mid)
return merge(mergeSort(fist), mergeSort(last))
function merge(left, right) {
var result = [];
while (left.length && right.length) {
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length)
result.push(left.shift());
while (right.length)
result.push(right.shift());
return result;
}
}
平⽅级复杂度,典型情况是当存在双重循环的时候,即把 O(n) 的代码再嵌套循环⼀遍,它的时间复杂度就是O(n²)了,代表应⽤是冒泡排序算法。
function bubleSort(arra){
var temp;
for(var i=0;i<arra.length;i++){
for(var j=0;j<arra.length-i-1;j++){
if(arra[j]>arra[j+1]){
temp=arra[j];
arra[j]=arra[j+1];
arra[j+1]=temp;
}
}
};
return arra;
}