【算法社区】从零开始的DS生活轻松从0基础写出Huffman树与红黑树-阿里云开发者社区

1.子孙结点和祖先结点：根的子树中任意节点称为该结点的子孙，结点的祖先是从根到该结点所经分支上的所有节点。
2.父结点,子结点,兄弟节点,堂兄弟节点：有子树的结点是其子树的根结点的父结点(双亲)；若A是B的父结点，B就是A的子结点；3.同双亲的孩子互称为兄弟；双亲是兄弟关系的节点称为堂兄弟（双亲在同层）。
4.结点的度：结点的子树个数。

5.树的度：树中所有结点中最大的度（树的叉）。

6.叶结点：度大于0的结点称为分支节点，度为0称为叶子节点又称终端节点。

7.路径和路径长度：树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的，而路径长度是路径上所经过的边的个数。

8.结点的层次,结点的深度,结点的高度,树的高度：结点的层次从树根开始定义，根结点为第1层，他的子结点尾第2层，以此类推。结点的深度是从根节点开始自顶向下逐层累加的。结点的高度是从叶结点开始自底向上逐层累加的。树的高度（深度）是树中结点的最大层数。

9.有序树和无序树：树中结点的各子树从左到右是有次序的，不能互换，称该树为有序树，否则称为无序树。

树的性质：

1.树中的结点数等于所有结点的度数加1

2.度为m的树中第i层至多有m^i-1个节点(i≥1)

3.高度为h的m叉树至多有(m^h - 1)/(m - 1)个结点

4.具有n各结点的m叉树的最小高度为 [logm(n(m - 1) + 1)]

5.一个N个结点的树只有N-1条边
6.除了根结点之外，每个结点之有且只有一个父结点

二叉树及其性质；普通树与二叉树的转换；

二叉树的定义：①度为2的树（树中所有结点中最大的度），②子树有左右顺序之分

// Definition for a binary tree node.
public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

二叉树的性质：

性质1:二叉树第i层上的结点数目最多为2^(i - 1) (i≥1)。

性质2:深度为k的二叉树至多有2^(k) - 1个结点(k≥1)。

性质3:包含n个结点的二叉树的高度至少为log2 (n+1)。

性质4:在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0 = n2 + 1。

满二叉树:

1.一棵深度为k且有2^k - 1个结点的二叉树

2.可以对满二叉树的结点进行连续编号，约定编号从根开始，自上而下，自左而右

完全二叉树:

深度为k的，有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应时，称为完全二叉树

完全二叉树特点:

1.叶子结点只可能出现在层次最大的两层上

2.对任一结点，若其右分支下子孙的最大层次为1，其左下分支的子孙的最大层次必为|或者1 + 1.

3.深度为k的完全二叉树第k层最少1个结点，最多2k - 1 - 1个结点:整棵树最少2k - 1个结点，最多2k - 2个结点

4.具有n个结点的完全二叉树的深度为[log2n] + 1

二叉树的转换；

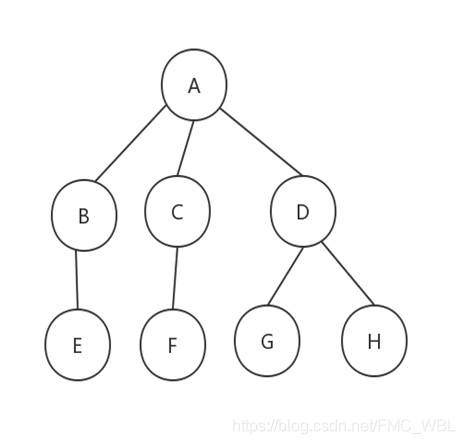
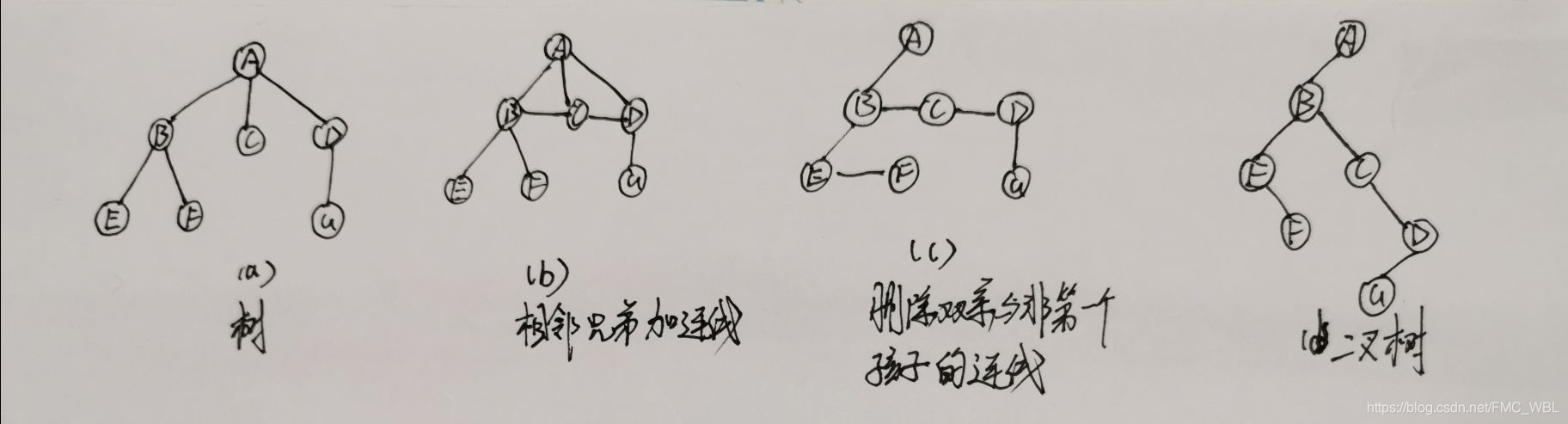
树转换为二叉树过程

1.树中所有相同双亲结点的兄弟结点之间加一条连线。

2.对树中不是双亲结点的第一个孩子的结点，只保留新添加的该结点与左兄弟结点之间的连线，删去该结点与双亲结点之间的连线。

3.整理所有保留的连线，根据连线摆放成二又树的结构，转换完成。

编辑

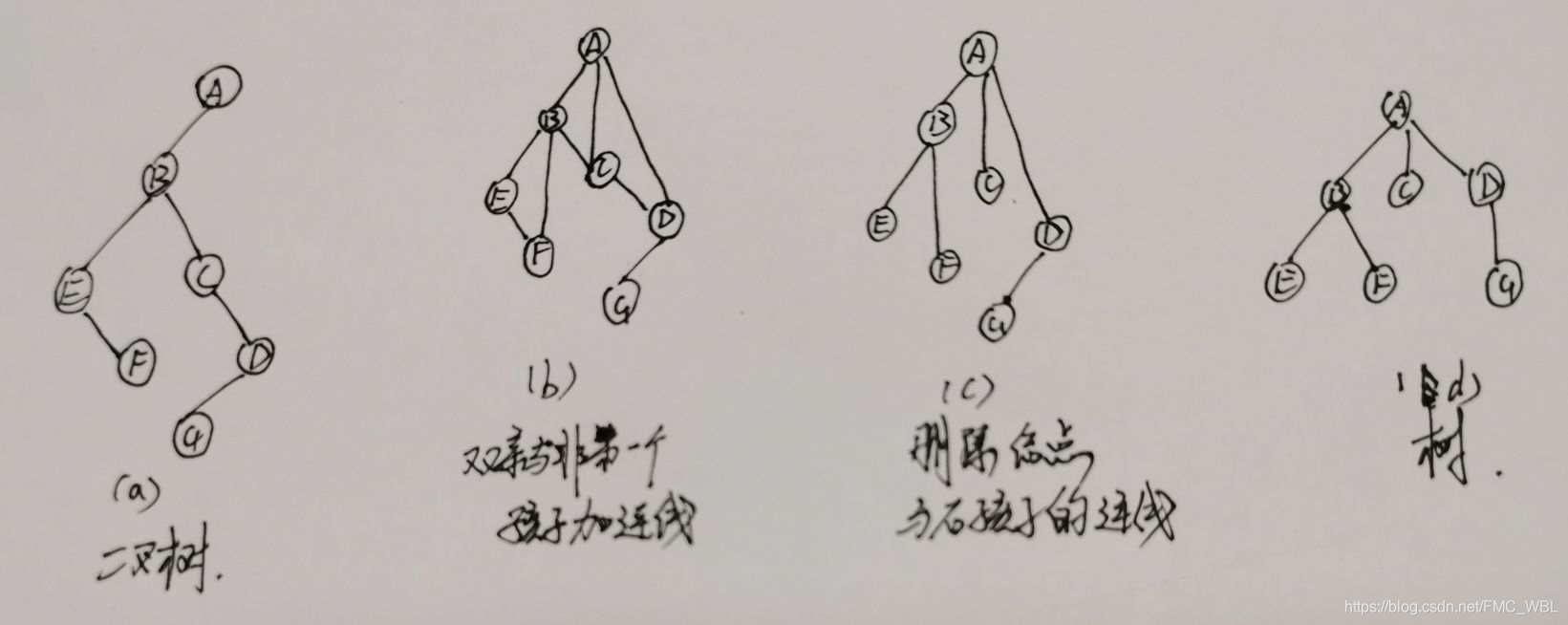
二叉树转换为树过程:

1.若某结点是其双亲结点的左孩子，则把该结点的右孩子，右孩子的右孩子都与该结点的双亲结点用线连起来:

2.删除原二叉树中所有双亲结点与右孩子结点的连线:

3.根据连线摆放成树的结构，转换完成。

编辑

树的前序，中序，后序，层次序遍历；

二叉树的遍历(traversing binary tree)按某神搜索路径寻访树中每个结点，使每个结点均被访向一次仅且一次。

1.先序遍历二叉树(根>左>右)

2.中序遍历二叉树(左>根>右)

3.后序遍历二叉树(左>右>根)

4.层序遍历二叉树

先序遍历，递归解法与非递归解法

/**
     * 首先，定义树的存储结构 TreeNode，Definition for a binary tree node.
     */
    public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int x) { val = x; }
    }
    /**
     * 递归解法
     * 思想： 先序遍历：根左右。先打印根节点，再递归左右子树，需要结合递归的函数调用栈理解
     */
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        // 输入根节点、list集合
        helper(root, list);
        return list;
    }
    // 利用 helper，加 list 条件
    private void helper(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        list.add(root.val); // 保存根节点
        if (root.left != null) {
            helper(root.left, list); // 遍历左子树
        }
        if (root.right != null) {
            helper(root.right, list); // 遍历右子树
        }
    }
    /**
     * 非递归解法-迭代法
     * 思想：迭代法，需要用到一个辅助栈
     */
    public List<Integer> preorderTraversalFunction(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<>(); // 存储节点
        List<Integer> list = new ArrayList<>(); // 保存遍历节点的顺序
        TreeNode curr = root; // 根节点
        while (curr != null || stack.size() > 0) {
            while (curr != null) {
                stack.push(curr);
                list.add(curr.val);
                curr = curr.left;
            }
            curr = stack.pop().right; // 当没有右子树时，只删除最上面节点
        }
        return list;
    }

迭代法思想图解：

编辑

树的存储结构,标准形式;完全树(complete tree)的数组形式存储；

1.双亲表示法：假设以一组连续空间存储数的结点，同时在每个结点中，附设一个指示器指示其双亲结点到链表中的位置。

data（数据域）	parent（指针域）
存储结点的数据信息存	储该结点的双亲所在数组中的下标

2.孩子表示法：把每个结点的孩子结点排列起来，以单链表作为存储结构，则n个结点有n个孩子链表，如果是叶子结点则此单链表为空。然后n个头指针又组成-个线性表，采用顺序存储结构，存放进一个一维数组中。孩子链表的孩子结点如下表1，表头数据的表头结点如下表2.

child（数据域）	next（指针域）
存储某个结点在表头数组中的下标	存储指向某结点的下一个孩子结点的指针

data（数据域）	firstchild（指针域）
存储某个结点的数据信息存	储该结点的孩子链表的头指针

3.孩子兄弟表示法：任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟存在也是唯一的。因此，设置两个指针，分别指向该结点的第一个孩子和此结点的右兄弟。

data（数据域）	firstchild（指针域）	rightsib
存储结点的数据信息	存储该结点的第一个孩子的存储地址	存储该结点的右兄弟结点的存储地址

树的应用,Huffman树的定义与应用；

Huffman树:构造一棵二叉树，该树的带权路径长度达到最小，称为最优二叉树，也称为哈夫曼树(Huffman Tree)

基本概念:

1.树的路径长度：从根到每一结点的路径长度之和。

2.结点的带权路径长度：从该结点到树根之间的路径长度与结点上权的乘积。

3.树的带权路径长度：树中所有叶子结点的带权路径长度之和，通常记做WPL。

构造方式：

每次把权值最小的两棵二叉树合并；左节点权值比右节点小；

Huffman算法：

1.由给定的n个权值{w0, w1, w2, .... wn-1},构造具有n棵二叉树的集合F= {T0,T1, T2, ... Tn-1},

其中每一棵二叉树Ti只有一个带有权值wi的根结点，其左、右子树均为空。

2.在F中选取两棵根结点的权值最小的二叉树,做为左、右子树构造一棵新的二叉树。置新的二叉

树的根结点的权值为其左、右子树，上根结点的权值之和。

3.在F中删去这两棵二叉树，加入新得的树。

4.重复(2)(3)，直到F只含一棵树为止。这棵树就是赫夫曼树

import java.util.ArrayList;
import java.util.List;
/**
 * @author 小明
 * 哈夫曼树
 */
public class HuffmanTree {
    //节点
    public static class Node<E> {
        E data; //数据
        int weight; //权重
        Node leftChild; //左子节点
        Node rightChild;//右子节点
        public Node(E data, int weight) {
            super();
            this.data = data;
            this.weight = weight;
        }
        public String toString() {
            return "Node[" + weight + ",data=" + data + "]";
        }
    }
    public static void main(String[] args) {
        List<Node> nodes = new ArrayList<Node>();
        //把节点加入至list中
        nodes.add(new Node("a", 10));
        nodes.add(new Node("b", 15));
        nodes.add(new Node("c", 12));
        nodes.add(new Node("d", 3));
        nodes.add(new Node("e", 4));
        nodes.add(new Node("f", 13));
        nodes.add(new Node("g", 1));
        //进行哈夫曼树的构造
        Node root = HuffmanTree.createTree(nodes);
        //打印哈夫曼树
        printTree(root);
    }
    /**
     * 构造哈夫曼树
     *
     * @param nodes 节点集合
     * @return 构造出来的哈夫曼树的根节点
     */
    private static Node createTree(List<Node> nodes) {
        //如果节点node列表中海油2个和2个以上的节点
        while(nodes.size()>1){
            //什么是最小的，list表进行排序，增序的方式， 0,1，
            sort(nodes);//排序方式是增序的
            Node left = nodes.get(0);//权重最小的
            Node right = nodes.get(1);//权重第二小的
            //生成一个新的节点（父节点），父节点的权重为两个子节点的之和
            Node parent = new Node(null,left.weight+right.weight);
            //树的连接，让子节点与父节点进行连接
            parent.leftChild = left;
            parent.rightChild = right;
            nodes.remove(0);//删除最小的
            nodes.remove(0);//删除第二小的。
            nodes.add(parent);
        }
        return nodes.get(0); //返回根节点
    }
    /**
     * 冒泡排序，用于对节点进行排序（增序排序）
     *
     * @param nodes
     */
    public static void sort(List<Node> nodes) {
        if (nodes.size() <= 1)
            return ;
        /*循环数组长度的次数*/
        for (int i = 0; i < nodes.size(); i++){
            /*从第0个元素开始，依次和后面的元素进行比较
             * j < array.length - 1 - i表示第[array.length - 1 - i]
             * 个元素已经冒泡到了合适的位置，无需进行比较，可以减少比较次数*/
            for (int j = 0; j < nodes.size() - 1 - i; j++){
                /*如果第j个节点比后面的第j+1节点权重大，交换两者的位置*/
                if (nodes.get(j + 1).weight < nodes.get(j).weight) {
                    Node temp = nodes.get(j + 1);
                    nodes.set(j+1,nodes.get(j));
                    nodes.set(j,temp);
                }
            }
        }
        return ;
    }
    /*
     * 递归打印哈夫曼树(先左子树，后右子树打印)
     */
    public static void printTree(Node root) {
        System.out.println(root.toString());
        if(root.leftChild !=null){
            System.out.print("left:");
            printTree(root.leftChild);
        }
        if(root.rightChild !=null){
            System.out.print("right:");
            printTree(root.rightChild);
        }
    }
}

树的高级数据结构,红黑树

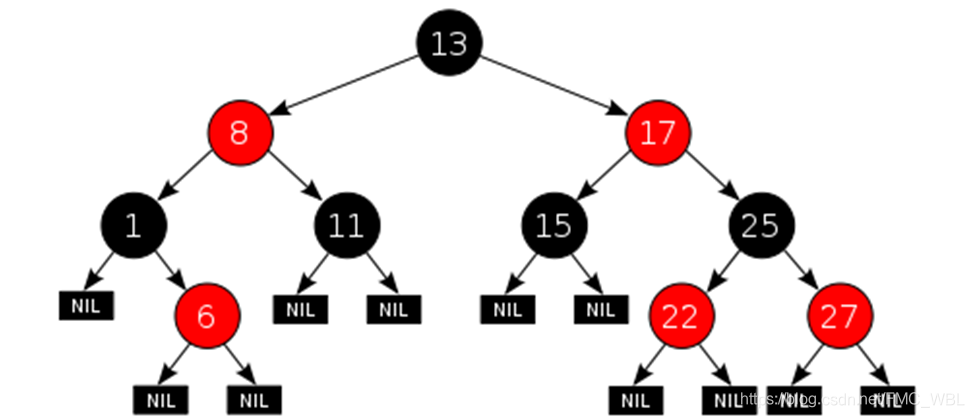
红黑树（R-B Tree，Red-Black Tree）它一种特殊的二叉查找树，同时具备以下特征：

1.节点非红即黑

2.根节点是黑色

3.所有NUll节点称为叶子节点，且认为颜色为黑

4.所有红色节点的子节点都为黑色

5.从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点

6.从根到叶子的最长的路径不多于最短的可能路径的两倍长（旋转的目的）

编辑

/**
 * @author 小明
 * 红黑树
 */
public class RBTree<T extends Comparable<T>> {
    private RBTNode<T> mRoot;    // 根结点
    private static final boolean RED   = false;//红色是false
    private static final boolean BLACK = true;//黑色是true
    public class RBTNode<T extends Comparable<T>> {
        boolean color;        // 颜色
        T key;                // 关键字(键值)
        RBTNode<T> left;    // 左孩子
        RBTNode<T> right;    // 右孩子
        RBTNode<T> parent;    // 父结点
        public RBTNode(T key, boolean color, RBTNode<T> parent, RBTNode<T> left, RBTNode<T> right) {
            this.key = key;
            this.color = color;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }
        public T getKey() {
            return key;
        }
        public String toString() {
            return ""+key+(this.color==RED?"(R)":"B");
        }
    }
    public RBTree() {
        mRoot=null;
    }
    private RBTNode<T> parentOf(RBTNode<T> node) {
        return node!=null ? node.parent : null;
    }
    private boolean colorOf(RBTNode<T> node) {
        return node!=null ? node.color : BLACK;
    }
    private boolean isRed(RBTNode<T> node) {
        return ((node!=null)&&(node.color==RED)) ? true : false;
    }
    private boolean isBlack(RBTNode<T> node) {
        return !isRed(node);
    }
    private void setBlack(RBTNode<T> node) {
        if (node!=null)
            node.color = BLACK;
    }
    private void setRed(RBTNode<T> node) {
        if (node!=null)
            node.color = RED;
    }
    private void setParent(RBTNode<T> node, RBTNode<T> parent) {
        if (node!=null)
            node.parent = parent;
    }
    private void setColor(RBTNode<T> node, boolean color) {
        if (node!=null)
            node.color = color;
    }
    /*
     * (递归实现)查找"红黑树x"中键值为key的节点
     */
    private RBTNode<T> search(RBTNode<T> x, T key) {
        if (x==null)
            return x;
        int cmp = key.compareTo(x.key);
        if (cmp < 0)
            return search(x.left, key);
        else if (cmp > 0)
            return search(x.right, key);
        else
            return x;
    }
    public RBTNode<T> search(T key) {
        return search(mRoot, key);
    }
    /*
     * (非递归实现)查找"红黑树x"中键值为key的节点
     */
    private RBTNode<T> iterativeSearch(RBTNode<T> x, T key) {
        while (x!=null) {
            int cmp = key.compareTo(x.key);
            if (cmp < 0)
                x = x.left;
            else if (cmp > 0)
                x = x.right;
            else
                return x;
        }
        return x;
    }
    public RBTNode<T> iterativeSearch(T key) {
        return iterativeSearch(mRoot, key);
    }
    /*
     * 查找最小结点：返回tree为根结点的红黑树的最小结点。
     */
    private RBTNode<T> minimum(RBTNode<T> tree) {
        if (tree == null)
            return null;
        while(tree.left != null)
            tree = tree.left;
        return tree;
    }
    public T minimum() {
        RBTNode<T> p = minimum(mRoot);
        if (p != null)
            return p.key;
        return null;
    }
    /*
     * 查找最大结点：返回tree为根结点的红黑树的最大结点。
     */
    private RBTNode<T> maximum(RBTNode<T> tree) {
        if (tree == null)
            return null;
        while(tree.right != null)
            tree = tree.right;
        return tree;
    }
    public T maximum() {
        RBTNode<T> p = maximum(mRoot);
        if (p != null)
            return p.key;
        return null;
    }
    /*
     * 找结点(x)的后继结点。即，查找"红黑树中数据值大于该结点"的"最小结点"。
     */
    public RBTNode<T> successor(RBTNode<T> x) {
        // 如果x存在右孩子，则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
        if (x.right != null)
            return minimum(x.right);
        // 如果x没有右孩子。则x有以下两种可能：
        // (01) x是"一个左孩子"，则"x的后继结点"为 "它的父结点"。
        // (02) x是"一个右孩子"，则查找"x的最低的父结点，并且该父结点要具有左孩子"，找到的这个"最低的父结点"就是"x的后继结点"。
        RBTNode<T> y = x.parent;
        while ((y!=null) && (x==y.right)) {
            x = y;
            y = y.parent;
        }
        return y;
    }
    /*
     * 找结点(x)的前驱结点。即，查找"红黑树中数据值小于该结点"的"最大结点"。
     */
    public RBTNode<T> predecessor(RBTNode<T> x) {
        // 如果x存在左孩子，则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
        if (x.left != null)
            return maximum(x.left);
        // 如果x没有左孩子。则x有以下两种可能：
        // (01) x是"一个右孩子"，则"x的前驱结点"为 "它的父结点"。
        // (01) x是"一个左孩子"，则查找"x的最低的父结点，并且该父结点要具有右孩子"，找到的这个"最低的父结点"就是"x的前驱结点"。
        RBTNode<T> y = x.parent;
        while ((y!=null) && (x==y.left)) {
            x = y;
            y = y.parent;
        }
        return y;
    }
    /*
     * 对红黑树的节点(x)进行左旋转
     *
     * 左旋示意图(对节点x进行左旋)：
     *      13                               17
     *     /  \                             /  \
     *   nul  17                          13    27
     *       / \      --(左旋)-.          / \    / \
     *     nul 27                      nul nul nul nul
     *         / \
     *      nul  nul
     */
    private void leftRotate(RBTNode<T> x) {
        // 设置x的右孩子为y
        RBTNode<T> y = x.right;
        // 将 “y的左孩子” 设为 “x的右孩子”；
        // 如果y的左孩子非空，将 “x” 设为 “y的左孩子的父亲”
        x.right = y.left;
        if (y.left != null)
            y.left.parent = x;
        // 将 “x的父亲” 设为 “y的父亲”
        y.parent = x.parent;
        if (x.parent == null) {
            this.mRoot = y;            // 如果 “x的父亲” 是空节点，则将y设为根节点
        } else {
            if (x.parent.left == x)
                x.parent.left = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
            else
                x.parent.right = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
        }
        // 将 “x” 设为 “y的左孩子”
        y.left = x;
        // 将 “x的父节点” 设为 “y”
        x.parent = y;
    }
    /*
     * 对红黑树的节点(8)进行右旋转
     *
     * 右旋示意图(对节点8进行右旋)：
     *            13                                 8
     *           /  \                             /     \
     *          8   nul                          1      13
     *         /  \      --(右旋)-              / \      / \
     *        1   nul                        nul nul nul  nul
     *       / \
     *     nul nul
     */
    private void rightRotate(RBTNode<T> y) {
        // 设置x是当前节点的左孩子。
        RBTNode<T> x = y.left;
        // 将 “x的右孩子” 设为 “y的左孩子”；
        // 如果"x的右孩子"不为空的话，将 “y” 设为 “x的右孩子的父亲”
        y.left = x.right;
        if (x.right != null)
            x.right.parent = y;
        // 将 “y的父亲” 设为 “x的父亲”
        x.parent = y.parent;
        if (y.parent == null) {
            this.mRoot = x;            // 如果 “y的父亲” 是空节点，则将x设为根节点
        } else {
            if (y == y.parent.right)
                y.parent.right = x;    // 如果 y是它父节点的右孩子，则将x设为“y的父节点的右孩子”
            else
                y.parent.left = x;    // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
        }
        // 将 “y” 设为 “x的右孩子”
        x.right = y;
        // 将 “y的父节点” 设为 “x”
        y.parent = x;
    }
    /*
     * 红黑树插入修正函数
     *
     * 在向红黑树中插入节点之后(失去平衡)，再调用该函数；
     * 目的是将它重新塑造成一颗红黑树。
     *
     * 参数说明：
     *     node 插入的结点        // 对应《算法导论》中的z
     */
    private void insertFixUp(RBTNode<T> node) {
        RBTNode<T> parent, gparent;
        // 若“父节点存在，并且父节点的颜色是红色”
        while (((parent = parentOf(node))!=null) && isRed(parent)) {
            gparent = parentOf(parent);//祖父节点
            //若“父节点”是“祖父节点的左孩子”
            if (parent == gparent.left) {
                RBTNode<T> uncle = gparent.right;
                if ((uncle!=null) && isRed(uncle)) { // 情况2：叔叔节点是红色
                    setBlack(uncle);
                    setBlack(parent);
                    setRed(gparent);
                    node = gparent;
                    continue;
                }
                // 情况5：叔叔是黑色，且当前节点是右孩子(两次旋转，先左后右)
                if (parent.right == node) {
                    RBTNode<T> tmp;
                    leftRotate(parent);  //左旋转
                    tmp = parent;
                    parent = node;
                    node = tmp;
                }
                // 情况3：叔叔是黑色，且当前节点是左孩子。（一次右旋转）
                setBlack(parent);
                setRed(gparent);
                rightRotate(gparent);
            } else {     //若“父节点”是“祖父节点的右孩子”
                RBTNode<T> uncle = gparent.left;
                if ((uncle!=null) && isRed(uncle)) {  // 情况2：叔叔节点是红色
                    setBlack(uncle);
                    setBlack(parent);
                    setRed(gparent);
                    node = gparent;
                    continue;
                }
                // 情况6：叔叔是黑色，且当前节点是左孩子(两次旋转，先右后左)
                if (parent.left == node) {
                    RBTNode<T> tmp;
                    rightRotate(parent);
                    tmp = parent;
                    parent = node;
                    node = tmp;
                }
                // 情况4：叔叔是黑色，且当前节点是右孩子。（一次左旋转）
                setBlack(parent);
                setRed(gparent);
                leftRotate(gparent);
            }
        }
        // 将根节点设为黑色
        setBlack(this.mRoot);
    }
    /*
     * 将结点插入到红黑树中
     *
     * 参数说明：
     *     node 插入的结点
     */
    private void insert(RBTNode<T> node) {
        int cmp;
        RBTNode<T> y = null;
        RBTNode<T> x = this.mRoot;
        // 1. 将红黑树当作一颗二叉查找树，将节点添加到二叉查找树中。
        while (x != null) {
            y = x;
            cmp = node.key.compareTo(x.key);
            if (cmp < 0)
                x = x.left;
            else
                x = x.right;
        }
        node.parent = y;
        if (y!=null) {
            cmp = node.key.compareTo(y.key);
            if (cmp < 0)
                y.left = node;
            else
                y.right = node;
        } else {
            this.mRoot = node;
        }
        // 2. 设置节点的颜色为红色
        node.color = RED;
        // 3. 将它重新修正为一颗二叉查找树
        insertFixUp(node);
    }
    /*
     * 新建结点(key)，并将其插入到红黑树中
     *
     * 参数说明：
     *     key 插入结点的键值
     */
    public void insert(T key) {
        RBTNode<T> node=new RBTNode<T>(key,BLACK,null,null,null);
        // 如果新建结点失败，则返回。
        if (node != null)
            insert(node);
    }
    /*
     * 红黑树删除修正函数
     *
     * 在从红黑树中删除插入节点之后(红黑树失去平衡)，再调用该函数；
     * 目的是将它重新塑造成一颗红黑树。
     *
     * 参数说明：
     *     node 待修正的节点
     */
    private void removeFixUp(RBTNode<T> node, RBTNode<T> parent) {
        RBTNode<T> other;
        while ((node==null || isBlack(node)) && (node != this.mRoot)) {
            if (parent.left == node) {
                other = parent.right;
                if (isRed(other)) {
                    // Case 1: x的兄弟w是红色的
                    setBlack(other);
                    setRed(parent);
                    leftRotate(parent);
                    other = parent.right;
                }
                if ((other.left==null || isBlack(other.left)) &&
                        (other.right==null || isBlack(other.right))) {
                    // Case 2: x的兄弟w是黑色，且w的俩个孩子也都是黑色的
                    setRed(other);
                    node = parent;
                    parent = parentOf(node);
                } else {
                    if (other.right==null || isBlack(other.right)) {
                        // Case 3: x的兄弟w是黑色的，并且w的左孩子是红色，右孩子为黑色。
                        setBlack(other.left);
                        setRed(other);
                        rightRotate(other);
                        other = parent.right;
                    }
                    // Case 4: x的兄弟w是黑色的；并且w的右孩子是红色的，左孩子任意颜色。
                    setColor(other, colorOf(parent));
                    setBlack(parent);
                    setBlack(other.right);
                    leftRotate(parent);
                    node = this.mRoot;
                    break;
                }
            } else {
                other = parent.left;
                if (isRed(other)) {
                    // Case 1: x的兄弟w是红色的
                    setBlack(other);
                    setRed(parent);
                    rightRotate(parent);
                    other = parent.left;
                }
                if ((other.left==null || isBlack(other.left)) &&
                        (other.right==null || isBlack(other.right))) {
                    // Case 2: x的兄弟w是黑色，且w的俩个孩子也都是黑色的
                    setRed(other);
                    node = parent;
                    parent = parentOf(node);
                } else {
                    if (other.left==null || isBlack(other.left)) {
                        // Case 3: x的兄弟w是黑色的，并且w的左孩子是红色，右孩子为黑色。
                        setBlack(other.right);
                        setRed(other);
                        leftRotate(other);
                        other = parent.left;
                    }
                    // Case 4: x的兄弟w是黑色的；并且w的右孩子是红色的，左孩子任意颜色。
                    setColor(other, colorOf(parent));
                    setBlack(parent);
                    setBlack(other.left);
                    rightRotate(parent);
                    node = this.mRoot;
                    break;
                }
            }
        }
        if (node!=null)
            setBlack(node);
    }
    /*
     * 删除结点(node)，并返回被删除的结点
     *
     * 参数说明：
     *     node 删除的结点
     */
    private void remove(RBTNode<T> node) {
        RBTNode<T> child, parent;
        boolean color;
        // 被删除节点的"左右孩子都不为空"的情况。
        if ( (node.left!=null) && (node.right!=null) ) {
            // 被删节点的后继节点。(称为"取代节点")
            // 用它来取代"被删节点"的位置，然后再将"被删节点"去掉。
            RBTNode<T> replace = node;
            // 获取后继节点
            replace = replace.right;
            while (replace.left != null)
                replace = replace.left;
            // "node节点"不是根节点(只有根节点不存在父节点)
            if (parentOf(node)!=null) {
                if (parentOf(node).left == node)
                    parentOf(node).left = replace;
                else
                    parentOf(node).right = replace;
            } else {
                // "node节点"是根节点，更新根节点。
                this.mRoot = replace;
            }
            // child是"取代节点"的右孩子，也是需要"调整的节点"。
            // "取代节点"肯定不存在左孩子！因为它是一个后继节点。
            child = replace.right;
            parent = parentOf(replace);
            // 保存"取代节点"的颜色
            color = colorOf(replace);
            // "被删除节点"是"它的后继节点的父节点"
            if (parent == node) {
                parent = replace;
            } else {
                // child不为空
                if (child!=null)
                    setParent(child, parent);
                parent.left = child;
                replace.right = node.right;
                setParent(node.right, replace);
            }
            replace.parent = node.parent;
            replace.color = node.color;
            replace.left = node.left;
            node.left.parent = replace;
            if (color == BLACK)
                removeFixUp(child, parent);
            node = null;
            return ;
        }
        if (node.left !=null) {
            child = node.left;
        } else {
            child = node.right;
        }
        parent = node.parent;
        // 保存"取代节点"的颜色
        color = node.color;
        if (child!=null)
            child.parent = parent;
        // "node节点"不是根节点
        if (parent!=null) {
            if (parent.left == node)
                parent.left = child;
            else
                parent.right = child;
        } else {
            this.mRoot = child;
        }
        if (color == BLACK)
            removeFixUp(child, parent);
        node = null;
    }
    /*
     * 删除结点(z)，并返回被删除的结点
     *
     * 参数说明：
     *     tree 红黑树的根结点
     *     z 删除的结点
     */
    public void remove(T key) {
        RBTNode<T> node;
        if ((node = search(mRoot, key)) != null)
            remove(node);
    }
    /*
     * 销毁红黑树
     */
    private void destroy(RBTNode<T> tree) {
        if (tree==null)
            return ;
        if (tree.left != null)
            destroy(tree.left);
        if (tree.right != null)
            destroy(tree.right);
        tree=null;
    }
    public void clear() {
        destroy(mRoot);
        mRoot = null;
    }
    /*
     * 打印"红黑树"
     *
     * key        -- 节点的键值
     * direction  --  0，表示该节点是根节点;
     *               -1，表示该节点是它的父结点的左孩子;
     *                1，表示该节点是它的父结点的右孩子。
     */
    private void print(RBTNode<T> tree, T key, int direction) {
        if(tree != null) {
            if(direction==0)    // tree是根节点
                System.out.printf("%2d(B) is root\n", tree.key);
            else                // tree是分支节点
                System.out.printf("%2d(%s) is %2d's %6s child\n", tree.key, isRed(tree)?"R":"B", key, direction==1?"right" : "left");
            print(tree.left, tree.key, -1);
            print(tree.right,tree.key,  1);
        }
    }
    public void print() {
        if (mRoot != null)
            print(mRoot, mRoot.key, 0);
    }
    /*
     * 前序遍历"红黑树"
     */
    private void preOrder(RBTNode<T> tree) {
        if(tree != null) {
            System.out.print(tree.key+" ");
            preOrder(tree.left);
            preOrder(tree.right);
        }
    }
    public void preOrder() {
        preOrder(mRoot);
    }
    /*
     * 中序遍历"红黑树"
     */
    private void inOrder(RBTNode<T> tree) {
        if(tree != null) {
            inOrder(tree.left);
            System.out.print(tree.key+" ");
            inOrder(tree.right);
        }
    }
    public void inOrder() {
        inOrder(mRoot);
    }
    /*
     * 后序遍历"红黑树"
     */
    private void postOrder(RBTNode<T> tree) {
        if(tree != null)
        {
            postOrder(tree.left);
            postOrder(tree.right);
            System.out.print(tree.key+" ");
        }
    }
    public void postOrder() {
        postOrder(mRoot);
    }
}

【算法社区】从零开始的DS生活轻松从0基础写出Huffman树与红黑树

导读（有基础的同学可以通过以下直接跳转到感兴趣的地方）

树的基本概念和术语

二叉树及其性质；普通树与二叉树的转换；

二叉树的转换；

树的前序，中序，后序，层次序遍历；

树的存储结构,标准形式;完全树(complete tree)的数组形式存储；

树的应用,Huffman树的定义与应用；

树的高级数据结构,红黑树

热门文章

最新文章

相关课程

相关电子书

相关实验场景

【算法社区】从零开始的DS生活 轻松从0基础写出Huffman树与红黑树

导读（有基础的同学可以通过以下直接跳转到感兴趣的地方）

树的基本概念和术语

二叉树及其性质；普通树与二叉树的转换；

二叉树的转换；

树的前序，中序，后序，层次序遍历；

树的存储结构,标准形式;完全树(complete tree)的数组形式存储；

树的应用,Huffman树的定义与应用；

树的高级数据结构,红黑树

热门文章

最新文章

相关课程

相关电子书

相关实验场景

【算法社区】从零开始的DS生活轻松从0基础写出Huffman树与红黑树