题注:《面试宝典》有相关习题,但思路相对不清晰,排版有错误,作者对此参考相关书籍和自己观点进行了重写,供大家参考。
(一)最短路径核心思想步骤如下:
(1)从选定的源顶点出发,先选择与该源顶点相连的权值最小且尚未标识过的顶点X,并标识X为True、记录该路径长度;
(2)然后比较经过该顶点X与其余顶点相连的路径之和是否小于源顶点到其余顶点的直接路径长度,是,则修改路径长度;否,则保持不变;
(3)循环执行(1),直至所有的顶点都标识为True。
为了便于理解,执行步骤图示如下几个表格。初始图结构表示如下:表格内值为顶点之间的权重,如(Vertex4,Vertex1)=10 代表顶点4与顶点1之间的路径权重为10。
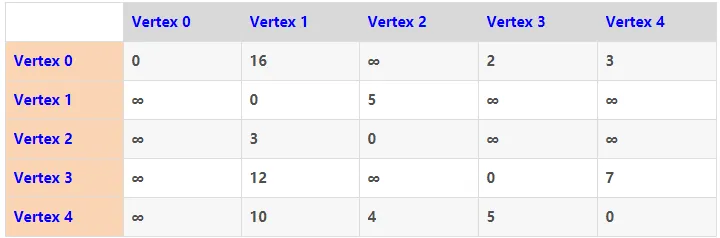
假定求解从顶点0到其余各顶点的最短路径长度。
前提:初始化操作,将0到各顶点的权重值存储到数组weights[][]中;将最小权重发现标识存储到数组weightFound[]中,并初始化weightFound[0]=true(因为0为源点)。
第1步:查找并选定顶点0到其余各顶点的最小权重值的顶点,且要求查找的点尚未被标识过true。显然,此处选择顶点Vertex3。
算法的执行步骤如下图所示:
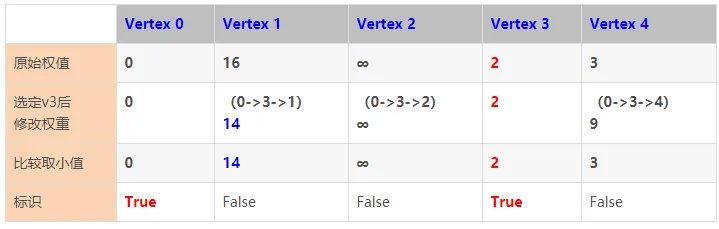
第2步:查找并选定顶点0到其余各顶点的最小权重值的顶点,且该点尚未被标识过true。
显然,此处选择顶点Vertex 4。
算法的执行步骤如下图所示:
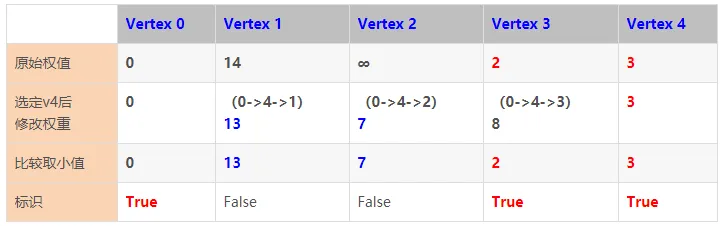
第3步:查找并选定顶点0到其余各顶点的最小权重值的顶点,且该点尚未被标识过true。
显然,此处选择顶点Vertex 2。
算法的执行步骤如下图所示:
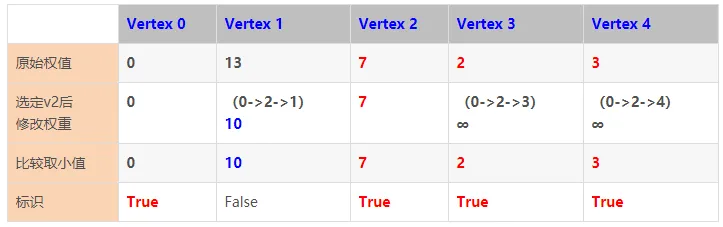
第4步:查找并选定顶点0到其余各顶点的最小权重值的顶点,且该点尚未被标识过true。
显然,此处选择顶点Vertex 1。
算法的执行步骤如下图所示:
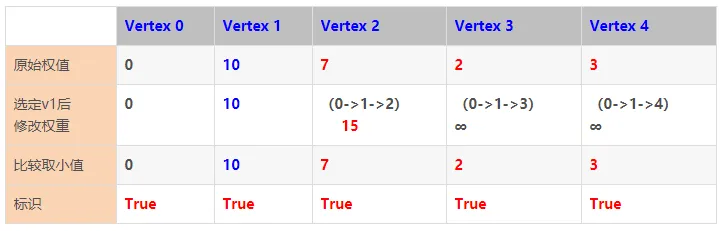
至此,所有标记都为True,比较结束。顶点0到其余各点的最短路径分别如下:

//inifinity 代表权值无穷大,即不可达。
int g_WeightMatrix[5][5] ={infinity,16,infinity,2,3,
infinity,infinity,5,infinity,infinity,
infinity,3,infinity,infinity,infinity,
infinity,12,infinity,infinity,7,
infinity,10,4,5,infinity};
template <class vType, int size>
class weightedGraphType : publicgraphType<vType, size>
{
public:
voidcreateWeightedGraph();
voidshortestPath(vType vertex);
voidprintShortestDistance(vType vertex);
protected:
intweights[size][size]; //权重矩阵
intsmallestWeight[size]; //源到其他顶点的最短路径
};1. 创建权重图
创建权重图的时候,我们做了简化处理。只是将给定的权重数组赋值过来了。[此处稍作修改,便可以改为手动输入顶点及邻接边的关系]。图的存储采用邻接矩阵的存储结构。
template <class vType, int size>
voidweightedGraphType<vType,size>::createWeightedGraph()
{
gSize= size;
for(int i = 0; i < size; i++)
{
smallestWeight[i]= 0;
for(int j =0; j < size; j++)
{
weights[i][j]= g_WeightMatrix[i][j];
cout<< weights[i][j] << "\t";
}
cout<< endl;
}
}2.求最短路径(1个源节点到其余结点Dijkstra算法)
template <class vType, int size>
voidweightedGraphType<vType,size>::shortestPath(vType vertex)
{
intv=0;
intminWeight;
//初始化 0代表到自身,infinity代表不可达.
//从结点vertex到j的权重记录在数组中
for(intj = 0; j < gSize; j++)
{
smallestWeight[j]= weights[vertex][j];
}
boolweightFound[size];
//权重是否应用标识...
for(intj = 0; j < gSize; j++)
{
weightFound[j]= false;
}
weightFound[vertex]= true; //初始设定
smallestWeight[vertex]= 0; //最小权重初始为0或infinity(不可达)
//结束标记——循环一遍(即:所有点都已经标识)。
//循环次数为gSize-2的原因是是vertex节点已经标识为true.
for(int i = 0; i < gSize-1; i++)
{
minWeight= infinity;
//从所有顶点中寻找权重最小且未被标识的顶点,
//v记录该顶点,minWeight记录权重值。
for(int j = 0; j < gSize; j++)
{
if(!weightFound[j])
{
if(smallestWeight[j]< minWeight)
{
v= j;
minWeight= smallestWeight[v];
}//endif
}//endif
}//endfor j
//标识点v已用.
weightFound[v]= true;
//利用已经标识的点v,判断经过v点的路径权重+(v->目的)
//权重值是否<已记录的smallestWeight。如果小,则替换;否则,不变。
for(int j = 0; j < gSize; j++)
{
if(!weightFound[j])
{
if(minWeight+ weights[v][j] < smallestWeight[j])
{
smallestWeight[j]= minWeight + weights[v][j];
}
}
}//endfor j(in)
}//endfor
}3.打印最短路径
//打印最短路径 源vertex结点到其余各个结点之间的路径...
template <class vType, int size>
voidweightedGraphType<vType,size>::printShortestDistance(vType vertex)
{
cout<< "Source vertex: " << vertex << endl;
cout<< "Shorest distance from source to each vertex" << endl;
cout<< "Vertex Shortest_Distance" << endl;
shortestPath(vertex);
for(int j = 0; j < gSize; j++)
{
cout<< setw(4) << j << setw(12) << smallestWeight[j]<< endl;
}
cout<< endl;
}作者:铭毅天下
来源:CSDN
原文:https://blog.csdn.net/laoyang360/article/details/7905674
版权声明:本文为博主原创文章,转载请附上博文链接!


