python高频面试问题(一)

整理一下高频率的面试问题。希望可以帮助一些朋友们。

1.python的基本数据类型

主要核心类型分为两类
不可变类型：
数字(int float bool complex),字符串(string)，元祖(tuple)，不可变集合(frozenset)。

可变类型:
列表（list），字典(dict),集合(set)
这里的可变不可变，是指内存中的值是否可以被改变

补充一点，其中不可变集合就是一个无序的不可变的集合,元素也只能是可hash的主要用来做字典的键，无序，元素不可重复，且元素只能是不可变类型。其次是元组并不是完全不可变的，如果元素含有list那么是可以添加元组里list的值的，原因就是添加元素的时候list的内存地址不会改变。另外过于字典的键值的问题，要求是可hash的所以字典的键值类型可以是int,string,tuple,和不可变集合。

2.python中的list去重复

这个就很简单了，首先转换成set，set的去重机制会完成去重然后再转回list即可，例如 去重list ,a=[1,2,3,44,5,6,5]

 new_a=list(set(a))

3.python中的集合操作问题

给定两个集合a={1,2,4,5},b={2,3,4,1,8}，求其补集，差集，并集。
首先我们先来了解set的基本运算有哪些

方法	符号	解释
a.update(b)	a|=b	并集,两个集合的去重后的合并
a.intersection_update(b)	a&=b	交集,两个集合相同的部分的集合
a.difference_update(b)	a-=b	差集a中有,b中没有的集合
a.symmetric_difference_update(b)	a^=b	对称差分,仅属于a或者仅属于b 上面的例子话是{3,5,8}
a.add(b)		加操作,这里会报错因为set是hash存储，必须存储不变的对象，例如字符串、数字、元组等。
a.remove(b)		删除操作 如果a里不包含b会引发异常
a.discard(b)		删除操作 如果a里不包含b不会引发异常，返回None
a.pop()		取出一个元素
a.clear()		清空列表

ok，上面的问题就可解决了，用符号&=,|=,-=就可以了

4.list合并

这个问题比较 需要注意的是list元素添加的区别
1.append() 向列表尾部追加一个新元素，列表只占一个索引位，在原有列表上增加
2.extend() 向列表尾部追加一个列表，将列表中的每个元素都追加进来，在原有列表上增加
3.+ 直接用+号看上去与用extend()一样的效果，但是实际上是生成了一个新的列表存这两个列表的和，只能用在两个列表相加上
4.+= 效果与extend()一样，向原列表追加一个新元素，在原有列表上增加
可以通过id属性查看内存地址的值，了解其运行状况。

5.正则表达是匹配url

import re

import requests

url="http://www.cnblogs.com"

s=requests.get(url).text()

ss=s.replace(" ","")

urls=re.findall(r"<a.*?href=.*?<\/a>",ss,re.I)

for i in urls:

print (i）

else:

print ('over')

另外附上几个网上搜到的验证Url地址的正则表达式

regex = re.compile(

r'^(?:http|ftp)s?://' # http:// or https://

r'(?:(?:[A-Z0-9](?:[A-Z0-9-]{0,61}[A-Z0-9])?\.)+(?:[A-Z]{2,6}\.?|[A-Z0-9-]{2,}\.?)|' #domain...

r'localhost|' #localhost...

r'\d{1,3}\.\d{1,3}\.\d{1,3}\.\d{1,3})' # ...or ip

r'(?::\d+)?' # optional port

r'(?:/?|[/?]\S+)$', re.IGNORECASE)

关于python使用re模块的第三个参数简单了解

re.I(re.IGNORECASE): 忽略大小写（括号内是完整写法）
re.M(re.MULTILINE): 多行模式，改变'^'和'$'的行为
re.S(re.DOTALL): 点任意匹配模式，改变'.'的行为

6.filter的使用

filter() 函数用于过滤序列，过滤掉不符合条件的元素，返回由符合条件元素组成的新列表。
该接收两个参数，第一个为函数，第二个为序列，序列的每个元素作为参数传递给函数进行判，然后返回 True 或 False，最后将返回 True 的元素放到新列表中。
以下是 filter() 方法的语法:
filter(function, iterable)

需要强调的是python3中filter返回的是一个filter对象。
下面一个例子是去除列表里面的偶数，其实map和reduce就可以实现这件事了。

def is_odd(n):

return n % 2 == 1

filter(is_odd, [1, 2, 4, 5, 6, 9, 10, 15])

#结果: [1, 5, 9, 15]

7 写一个实现斐波那契的方法

斐波那契数列的定义
f(0) = 1,f(1) = 1,f(n) = f(n-1) + f(n-2)
最好理解的写法递归时间复杂度最大的。

# 递归

def Fibonacci_Recursion_tool(n):

if n <= 0:

return 0

elif n == 1:

return 1

else:

return Fibonacci_Recursion_tool(n - 1) + Fibonacci_Recursion_tool(n - 2)

一般写的最多的是这样

def fib(n):  

x,y=0,1  

while(n):  

x,y,n=y,x+y,n-1  

return x 

yield的关键字实现

def Fibonacci_Yield_tool(n):

a, b = 0, 1

while n > 0:

yield b

a, b = b, a + b

n -= 1

def Fibonacci_Yield(n):

# return [f for i, f in enumerate(Fibonacci_Yield_tool(n))]

return list(Fibonacci_Yield_tool(n))

尾递归

def fib(n):

def fib_iter(n,x,y):

if n==0 : return x

else : return fib_iter(n-1,y,x+y)

return fib_iter(n,0,1)

上述代码简化

fib=lambda n,x=0,y=1:x if not n else f(n-1,y,x+y)

下面是效率最高矩阵实现，时间复杂度才logn，仅供参考

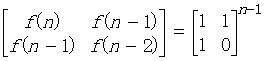
Step1: n=2时

Step2：设n=k时，公式成立，则有：

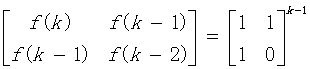
等式两边同乘以[1,1;1,0]矩阵可得：

左=右，这正是n=k+1时的形式，即当n=k+1时等式成立。

 

由Step1和Step2可知，该数学公式成立。

由此可以知道该问题转化为计算右边矩阵的n-1幂问题.
我们利用分治的算法思想可以考虑如下求解一个数A的幂。

以上内容来自:https://www.cnblogs.com/python27/archive/2011/11/25/2261980.html

python代码实现

def multi(a,b):

c=[[0,0],[0,0]]

for i in range(2):

for j in range(2):

for k in range(2):

c[i][j]=c[i][j]+a[i][k]*b[k][j]

return c

def matrix(n):

base=[[1,1],[1,0]]

ans=[[1,0],[0,1]]

while n:

if n&1:

ans=multi(ans,base)

base=multi(base,base)

n>>=1

return ans[0][1]

print(matrix(100))

8.列表排序

这里就使用时间复杂度为O(nlogn)的快速排序

def quick_sort(array, left, right):  

if left >= right:  

return  

low = left  

high = right  

key = array[low]  

while left < right:  

while left < right and array[right] > key:  

right -= 1  

array[left] = array[right]  

while left < right and array[left] <= key:  

left += 1  

array[right] = array[left]  

array[right] = key  

quick_sort(array, low, left - 1)  

quick_sort(array, left + 1, high)  

关于8大排序算法的一些比较参考:https://www.cnblogs.com/woider/p/6835466.html

9.切片的使用

切片操作要提供三个参数 [start_index: stop_index: step] 
start_index是切片的起始位置
stop_index是切片的结束位置（不包括）
step可以不提供，默认值是1，步长值不能为0，不然会报错ValueError。
当 step 是正数时，以list[start_index]元素位置开始， step做为步长到list[stop_index]元素位置（不包括）为止，从左向右截取， 
start_index和stop_index不论是正数还是负数索引还是混用都可以，但是要保证 list[stop_index]元素的【逻辑】位置
必须在list[start_index]元素的【逻辑】位置右边，否则取不出元素。

例如，如何获取一个列表的后两个元素
a=[1,2,3,4,6,8]
new_a=a[-2:]

当 step 是负数时，以list[start_index]元素位置开始， step做为步长到list[stop_index]元素位置（不包括）为止，从右向左截取，
start_index和stop_index不论是正数还是负数索引还是混用都可以，但是要保证 list[stop_index]元素的【逻辑】位置
必须在list[start_index]元素的【逻辑】位置左边，否则取不出元素。

alist = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
alist[-1: -5: -1]

假设list的长度（元素个数）是length, start_index和stop_index在符合虚拟的逻辑位置关系时，
start_index和stop_index的绝对值是可以大于length的。比如下面两个例子：
alist = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
alist[-11:11]

该部分内容来自:https://blog.csdn.net/xpresslink/article/details/77727507

10.二分法查找

二分法是一种快速查找的方法，时间复杂度低，逻辑简单易懂，总的来说就是不断的除以2除以2… 二分法查找非常快且非常常用，但是唯一要求是要求数组是有序的,关于排序请参考第8条列表排序

代码实现

#!/usr/bin/python3.6

# -*- coding: utf-8 -*-

def BinarySearch(arr, key):

# 记录数组的最高位和最低位

min = 0

max = len(arr) - 1

if key in arr:

# 建立一个死循环，直到找到key

while True:

# 得到中位数

# 这里一定要加int，防止列表是偶数的时候出现浮点数据

center = int((min + max) / 2)

# key在数组左边

if arr[center] > key:

max = center - 1

# key在数组右边

elif arr[center] < key:

min = center + 1

# key在数组中间

elif arr[center] == key:

print(str(key) + "在数组里面的第" + str(center) + "个位置")

return arr[center]

else:

print("没有该数字!")

if __name__ == "__main__":

arr = [1, 6, 9, 15, 26, 38, 49, 57, 63, 77, 81, 93]

while True:

key = input("请输入你要查找的数字：")

if key == " ":

print("谢谢使用！")

break

else:

BinarySearch(arr, int(key))

该部分内容来自:https://www.cnblogs.com/bfyin/p/6404173.html