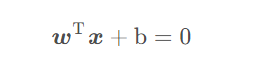支持向量机(一)+https://developer.aliyun.com/article/1544107?spm=a2c6h.13148508.setting.15.1fa24f0ewU5jCe
Demo实践 我们利用sklearn直接调用 SVM函数进行实践尝试
库函数导入
import numpy as np import matplotlib.pyplot as plt import seaborn as sns from sklearn import svm
构建数据集并进行模型训练
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]]) y_label = np.array([0, 0, 0, 1, 1, 1]) svc = svm.SVC(kernel='linear') svc = svc.fit(x_fearures, y_label)
模型参数查看
svc.coef_ svc.intercept_
模型预测
y_train_pred = svc.predict(x_fearures) y_train_pred
可视化
x_range = np.linspace(-3, 3) w = svc.coef_[0] a = -w[0] / w[1] y_3 = a*x_range - (svc.intercept_[0]) / w[1] plt.figure() plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis') plt.plot(x_range, y_3, '-c') plt.show()
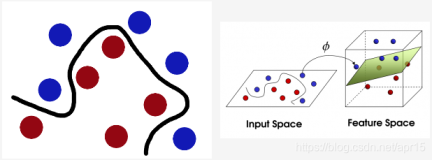
当存在线性不可分的场景时,我们需要使用核函数来提高训练样本的维度、或者将训练样本投向高维。
高斯核(RBF):一般是通过将样本投射到无限维空间,使得原来不可分的数据变得可分。
SVM 默认使用 RBF 核函数,将低维空间样本投射到高维空间。
支持向量机的总结:
优点:
- 可以解决高维数据问题,因为支持向量机通过核函数将原始数据映射到高维空间。
- 对非线性问题具有较好的处理能力,通过引入核函数,支持向量机可以处理非线性可分的数据。
- 鲁棒性较好,支持向量机只关心距离超平面最近的支持向量,对其他数据不敏感,因此对噪声数据具有较强的抗干扰能力。
缺点:
- 对于大规模数据集,支持向量机的训练时间较长,因为需要求解一个二次规划问题。
- 对参数和核函数的选择敏感,不同的参数和核函数可能导致模型性能差异较大,需要进行参数调优。
- 对于线性不可分的数据,需要引入核函数,但选择合适的核函数并不容易。
支持向量机是一种强大的机器学习算法,具有广泛的应用前景。在实际应用中,需要根据具体问题选择合适的核函数和参数,以达到最佳的预测性能。