没错,本篇是上一篇《好的,BFS,又学废了!》的姊妹篇,意在通过简单回顾拾起学了忘、又忘了学的基础数据结构;
DFS,全称是:深度优先遍历(Depth_First_Search),通常和 BFS 广度优先遍历(Breadth-first search)对比理解学习;
还记得,前篇最后小结中的一句话:
BFS,是一种利用队列实现的搜索算法。(与之相对的 DFS 是用栈来处理)
没错!再次强化理解:
- DFS 采用的是栈的形式, 即先进后出;
- BFS 则采用的是队列的形式, 即先进先出;
深度优先不需要记住所有的节点, 所以占用空间小, 而广度优先需要先记录所有的节点占用空间大;
题外话:需要的空间大,则需要的时间就更少;占用的空间小,则需要的时间就更多,时间换空间,或者空间换时间;可以联想到,在函数式编程和非函数式编程中也有这个思想,FP语言所占内存大,惰性求值,时间上,计算更快、更合理;非FP语言,所占内存小,变量频繁修改,所占内存小,但时间消耗更多;
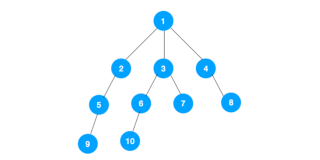
OK,一图胜千言:
可以看到,DFS 深度优先遍历不像 BFS 广度优先遍历那样逐层遍历,而是 “一条路上走到黑”、“不撞南墙不回头” 的态势纵向遍历所有的子节点,再返回兄弟节点,再遍历兄弟节点的子节点,直接全部遍历结束;
小例子仍然以遍历 DOM 树为需求,用 DFS 解:
function deepFirstSearch(node) { var nodes = []; if (node != null) { var stack = []; // 栈! stack.push(node); // 入栈 while (stack.length != 0) { var item = stack.pop(); // 将最后一个元素出栈 nodes.push(item); // 推到结果数组 var children = item.children; for (var i = children.length - 1; i >= 0; i--) stack.push(children[i]); // 子元素入栈 } } return nodes; } deepFirstSearch(document.getElementsByTagName("body")[0])
递归实现:
function deepFirstSearch(node,nodeList) { if (node) { nodeList.push(node); var children = node.children; for (var i = 0; i < children.length; i++) //每次递归的时候将 需要遍历的节点 和 节点所存储的数组传下去 deepFirstSearch(children[i],nodeList); } return nodeList; } deepFirstSearch(document.getElementsByTagName("body")[0],[])
为了更加明显的对比,贴出之前 BFS 的解:
function breadthFirstSearch(node) { var nodes = []; if (node != null) { var queue = []; queue.unshift(node); // 将初始节点放入队中 while (queue.length != 0) { var item = queue.shift(); // 提取队首元素 nodes.push(item); var children = item.children; for (var i = 0; i < children.length; i++) // 遍历全部子元素 queue.push(children[i]); // 推入队中 } } return nodes; } breadthFirstSearch(document.getElementsByTagName("body")[0])
递归实现:
function breadthFirstSearch(node,nodes) { if (!(node == null)) { nodes.push(node); breadthFirstSearch(node.nextElementSibling,nodes); // 优先遍历兄弟节点 breadthFirstSearch(node.firstElementChild,nodes); // 再遍历子节点 } return nodes; } breadthFirstSearch(document.getElementsByTagName("body")[0],[])
综上,需谨记:DFS-栈、BFS-队列;
简单来道题吧:二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例: 给定二叉树 [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 返回它的最大深度 3 。
思路:节点为空时说明高度为 0,所以返回 0;节点不为空时则分别求左右子树的高度的最大值,同时加1表示当前节点的高度,返回该数值;
递归解:
/** * Definition for a binary tree node. * function TreeNode(val) { * this.val = val; * this.left = this.right = null; * } */ /** * @param {TreeNode} root * @return {number} */ var maxDepth = function(root) { if(!root) { return 0; } else { const left = maxDepth(root.left); const right = maxDepth(root.right); return Math.max(left, right) + 1; } };
时间复杂度:O(n)
递归解二叉树,yyds!
BFS 和 DFS 是很重要的算法,BFS 的重点在于队列,而 DFS 的重点在于递归;它们在搜素领域有非常大的发挥空间。
BFS 常用于找单一的最短路线,它的特点是 "搜到就是最优解",而 DFS 用于找所有解的问题,它的空间效率高,而且找到的不一定是最优解,必须记录并完成整个搜索,故一般情况下,深搜需要非常高效的剪枝;什么是算法中的剪枝?
OK,以上就是本次分享;