🍃1. 算法思想
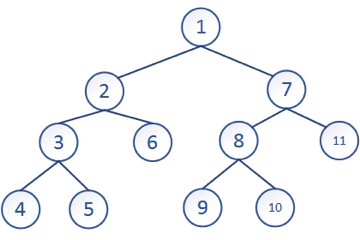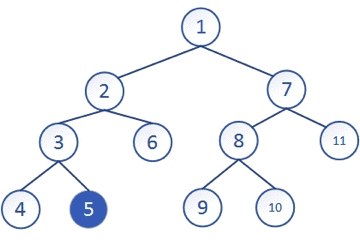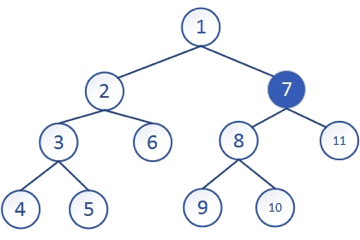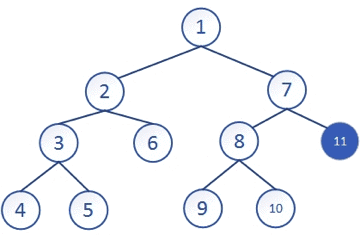
DFS算法的基本思想是从图中的某个顶点v出发,访问此顶点,然后依次从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到。若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,整个进程反复进行直到所有顶点都被访问为止。
从上图中可以直观的感受到这种思想
就是一条路走到黑的思想,走到无路可走再回退到上一层,再选择另一条路继续一直走,再回退,直到整个遍历完成,深度优先搜索一般是通过递归来实现的,“递”的过程就是往下搜的过程对应着深度,“归”的过程就是回溯,回退上一级
🍃2. 三种枚举方式
🍃2.1 指数型枚举
指数型枚举是指一共有n个数,每一个数都有两种状态,也就是选或不选,时间复杂度也就是2^n,指数级的
例如3个数的枚举时,每一个数都有选和不选两种状态,可以根据这个画出递归搜索树
接着用代码实现一下
using namespace std; int n; int vis[20]; void dfs(int x){ //表示已经n个数都被判断过了,一种方案已经搜索完成 if(x > n){ for(int i = 1;i <= n;i++){ if(vis[i] == 1) cout<<i<<" "; } cout<<'\n'; return; } vis[x] = 2;//表示不选 dfs(x+1);//继续搜下一个 vis[x] = 0;//回溯 vis[x] = 1;//表示选 dfs(x+1);//继续搜下一个 vis[x] = 0;//回溯 } int main(){ cin>>n; dfs(1); return 0; }
🍃2.2 排列型枚举
排列型枚举是一种生成给定集合所有可能排列的方法,其实在中学阶段我们就学过排列组合的问题,排列是区分顺序的,例如,同样是1 2 3三个数字,1,2, 3和 1,3,2是两种方案。
来看下面的一个例题:
很简单,就是生成n个数字的全排列方案,在用代码实现的过程中,需要另外再开一个vis数组,表示状态,以此来区分是否被选过
using namespace std; int vis[15]; int a[15]; int n; void dfs(int x){ //表示n个数字都已经选过了 if(x > n){ for(int i = 1;i <= n;i++){ cout<<setw(5)<<a[i];//题目中要求5个场宽 } cout<<'\n'; return; } for(int i = 1;i <= n;i++){ if(!vis[i]){ vis[i] = 1;//选过标记为1 a[x] = i;//表示该数字被选上了 dfs(x+1);//继续选下一个数字 vis[i] = 0;//回溯重置该数字的状态 a[x] = 0;//,也可以不写,因为数据可以直接覆盖 } } } int main(){ cin>>n; dfs(1); return 0; }
也就是依次枚举n个数,当这n个数选出一种方案之后,就回溯,再判断其它分支
🍃2.3 组合型枚举
组合是从n个不同元素中取出m(m≤n)个元素的所有取法,组合不考虑元素的顺序。也就是 1 2 3 和 1 3 2是同一种方案
这次的dfs中采用了两个参数,一个表示枚举了几个数,一个表示从哪个数开始往后选,因为这次是组合型枚举,例如,在选了1 3 2之前,1 2 3肯定也已经选过了,所以不会有1 3 2这种情况出现,从哪个数开始往后选,都是选的比这个数字典序大的数,不存在字典数大的数排在字典数小的之前的情况,所以要记录从哪个数开始往后选
using namespace std; int a[25]; int n,r; void dfs(int x,int start){ //已经选够的情况 if(x > r){ for(int i = 1;i<=r;i++){ cout<<setw(3)<<a[i]; } cout<<'\n'; return; } for(int i = start;i<=n;i++){ a[x] = i; dfs(x+1,i+1);//选下一个数字,并且下一个数字的字典序要比本次大,也就是从i+1开始往后选 a[x] = 0; } } int main(){ cin>>n>>r; dfs(1,1); return 0; }
🍃3. 剪枝优化
在深度优先搜索(DFS)中,剪枝是一种常用的优化技术,用于减少不必要的搜索空间,从而提高搜索效率。剪枝的核心思想是在搜索过程中,尽早地识别和排除那些不可能产生解的路径或状态,从而避免在这些无效路径上浪费时间和资源。
dfs(深度优先搜索)其实是一种特别暴力的算法,也就是我们常说的暴力搜索,时间复杂度一般都是指数级或阶乘级的这样,这时,剪枝就显得尤为重要,不然特别容易超时
来看一道洛谷的典型题:P1088:火星人
这题是不是就是我们之前讲到的全排列类型的题,意思就是给出一个排列方式,按照字典序求这种方式以后的第几种排列
这次用Java实现一下:
public class Main { static int n = 0, r = 0;//n个数字,求第r中排列方式 static int cnt = 0;//记录次数 static int[] arr = new int[10010]; static int[] mars = new int[10010];//火星人的排列 static boolean[] vis = new boolean[10010];//记录状态 static boolean falg = false;//记录状态,后面用于剪枝 public static void main(String[] args) { Scanner sc = new Scanner(System.in); n = sc.nextInt(); r = sc.nextInt(); for (int i = 1; i <= n; i++) { mars[i] = sc.nextInt(); } dfs(1); } public static void dfs(int x) { //剪枝,后面的不用再去排列了 if (falg) { return; } if (x > n) { cnt++; if (cnt == r + 1) { //表示已经找到了答案 falg = true; for (int i = 1; i <= n; i++) { System.out.print(arr[i] + " "); } System.out.println(); } return; } //和之前写的排列模板一样 for (int i = 1; i <= n; i++) { //表示从火星人给出的排列方案开始往后搜索 if (cnt == 0) { i = mars[x]; } if (!vis[i]) { arr[x] = i; vis[i] = true; dfs(x + 1); vis[i] = false; } } } }
这道题我们就很好的利用了剪枝进行优化,不然按照原来算法的时间复杂度肯定是会超时的,当我们找到目标方案之后,后面的方案就没必要进行搜索了,此时直接退出函数,也就是剪枝
每一题的剪枝方案需要具体题目具体分析。
🍃4. 图的搜索
步骤:
1.选择起始点:从图的某个顶点v开始。
2.标记当前顶点:将当前顶点v标记为已访问,以避免重复访问。
3.遍历邻接点:对于v的每个未访问的邻接点w,递归地执行DFS,从w开始。
4.回溯:当没有更多的邻接点可以遍历时,返回到上一步的顶点。
下面看一道例题:
图的存储:通过二维数组进行存储
怎么往四个方向进行搜索:定义两个方向数组
using namespace std; const int N = 25; char arr[N][N]; bool vis[N][N]; int res; int x, y; //方向数组,四个方向进行搜索 int dx[4] = { -1,0,1,0 }; int dy[4] = { 0,1,0,-1 }; void dfs(int m,int n){ for(int i = 0;i < 4;i++){ int a = m + dx[i]; int b = n + dy[i]; if(vis[a][b]) continue; if(arr[a][b] != '.')continue;//只能走"." if(a < 0 || a >= x) continue;//不能越界 if(b < 0 || b >= y) continue; vis[a][b] = true; res++; dfs(a,b);//本题不需要回溯,直接往下搜 } } int main(){ ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); cin >> y >> x; for (int i = 0; i < x; i++) { for (int j = 0; j < y; j++) { cin >> arr[i][j]; } } for (int i = 0; i < x; i++) { for (int j = 0; j < y; j++) { //从起点开始搜索 if (arr[i][j] == '@') { vis[i][j] = true; dfs(i, j); } } } cout << res + 1;//加上起点 return 0; }
🍃5. 来几道题试试手
🍃5.1 选数
做题点这里👉 : 洛谷P1036
这道题其实还是之前讲过的组合型枚举,例如样例中是4个数里边选3个进行组合,只不过最后多了一个求和和素数判断
还用Java来实现一下:
public class Main { static int n = 0,k = 0; static int cnt = 0; static int[] arr = new int[50]; static int[] res = new int[20]; public static void main(String[] args) { Scanner sc = new Scanner(System.in); n = sc.nextInt(); k = sc.nextInt(); for(int i = 1;i <= n;i++){ arr[i] = sc.nextInt(); } dfs(1,1); System.out.println(cnt); } public static boolean isPrime(int num){ for(int i=2;i*i<=num;i++){ if(num%i==0) return false; } return true; } public static void dfs(int x, int start){ if(x == k + 1){ int sum = 0; //求和 for(int i =1;i <= k;i++){ sum += res[i]; } //判断素数,方案数+1 if(isPrime(sum)){ cnt++; } return; } for(int i = start;i <= n;i ++){ res[x] = arr[i]; dfs(x + 1,i + 1); res[x] = 0; } } }
🍃5.2 火柴棒等式
做题点这里👉 : 洛谷1149
我们来实现一下:
import java.util.Scanner; public class Main { static int[] match = new int[1000]; static int[] arr = new int[1000]; static int n = 0, cnt = 0; public static void main(String[] args) { Scanner sc = new Scanner(System.in); n = sc.nextInt(); n -= 4;//等号和加号用的火柴棒 match[0] = 6; match[1] = 2; match[2] = 5; match[3] = 5; match[4] = 4; match[5] = 5; match[6] = 6; match[7] = 3; match[8] = 7; match[9] = 6; //计算10以后的数字用到的火柴帮数量 for (int i = 10; i < 1000; i++) { match[i] = match[i % 10] + match[i / 10]; } dfs(1, 0); System.out.println(cnt); } public static void dfs(int x, int sum) { //超过给出的数量,剪枝 if (sum > n) { return; } if (x > 3) { if (sum == n && arr[1] + arr[2] == arr[3]) { cnt++; } return; } for (int i = 0; i < 1000; i++) { arr[x] = i; dfs(x + 1, sum + match[i]); arr[x] = 0; } } }