
如何使用叉积来计算一个平面的法向量?
版权声明:本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单进行举报,一经查实,本社区将立刻删除涉嫌侵权内容。
在三维空间中,一个平面的法向量可以通过计算两个不共线的向量的叉积来获得。以下是计算平面法向量的步骤:
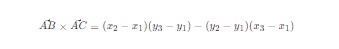
然后,单位化这个叉积向量: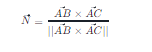
其中 (||\vec{AB} \times \vec{AC}||) 是叉积向量的模。
最终得到的 (\vec{N}) 就是平面的法向量。
首先选取平面上的两个非共线向量(例如,通过平面上的三个点v1, v2, v3,可以构造向量ab = v2 - v1和ac = v3 - v1)。然后,计算这两个向量的叉积得到一个新的向量,该向量即为平面的法向量。注意,叉积的结果需要除以自身的模长来得到单位法向量。例如:
java
Vertex ab = new Vertex(v2.x - v1.x, v2.y - v1.y, v2.z - v1.z);
Vertex ac = new Vertex(v3.x - v1.x, v3.y - v1.y, v3.z - v1.z);
// 法向量
Vertex norm = new Vertex(
ab.y ac.z - ab.z ac.y,
ab.z ac.x - ab.x ac.z,
ab.x ac.y - ab.y ac.x
);
double normalLength = Math.sqrt(norm.x norm.x + norm.y norm.y + norm.z * norm.z);
norm.x /= normalLength;
norm.y /= normalLength;
norm.z /= normalLength;