
如何找到合适的 a、b 值:抛物线的最低端?
版权声明:本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单进行举报,一经查实,本社区将立刻删除涉嫌侵权内容。
以线性函数为例,训练算法实际上就是在寻找合适的 a,b 值。如果我们在茫茫的数字海洋中随机寻找 a,b 的值那应该是永远找不到的了。这时候我们就需要用到梯度下降算法来寻找 a,b 值了。
再明确一下目标,将上述的损失值计算公式替换为:y=ax+b // 函数 2 const cost = (((ax1+b)-y1)^2 + ((ax2+b)-y2)^2 + ((ax3+b)-y3)^2 + ((ax4+b)-y4)^2 + ((ax5+b)-y5)^2 + ((ax6+b)-y6)^2 )/ 6 目标是找到一组 a、b 的值使得 cost 最小。有了这个目标就好办多了。 初中的抛物线函数,也就是一元二次方程:y = ax^2+bx+c 而我们上述的 cost 函数虽然看起来很长,但是正好也是一个二次函数。它的图大概是这样的: 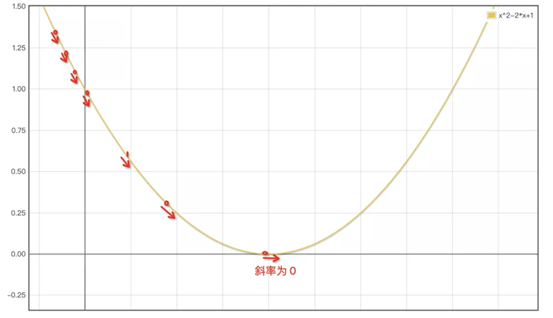
只要我们找到最低点的 a,b 值就完成我们的目标了。