
由零个或多个数据元素组成的有限序列
注意:

请问公司的组织架构是否属于线性关系?
分析:一般公司的总经理管理几个总监,每个总监管理几个经理,每个经理都有各自的下属和员工。
那这样的组织架构当然不是线性关系了,事实上后面你就会知道,这是一个树状结构。
注意线性关系的条件是如果存在多个元素,则”第一个元素无前驱,而最后一个元素无后继,其他元素都有且只有一个前驱和后继。“
那么班里同学之间的友谊是否属于线性关系?
当然也不是了,因为每个人都会跟许多同学建立纯纯的友谊关系。
情侣之间的爱情关系呢?
哈哈,当然是扯淡,这要是线性关系,也就不会有所谓的第三者插足了。。。你们的爱情关系定会是线性关系!
最后一题,一个班级的点名册,是不是线性表?
是啦,看下表:
| 学号 | 姓名 | 性别 | 职位 |
|---|---|---|---|
| 1 | 景禹 | 男 | 班长 |
| 2 | 哒哒 | 女 | 副班长 |
| 3 | 花花 | 女 | 音乐课代表 |
| 4 | 素素 | 女 | 美术课代表 |
| 5 | 明明 | 男 | 小组长 |
数据类型: 是指一组性质相同的值的集合及定义在此集合上的一些操作的总称。(官方定义)
例如很多编程语言的整型,浮点型,字符型这些指的就是数据类型
当年那些设计计算机语言的人,为什么会考虑到数据类型呢?
比如,大家需要住房子,也都希望房子越大越好。但显然,没有多少钱的话考虑房子是没啥意义的。于是商品房出现了各种各样的房型,有别墅的,有错层的,有单层的,甚至在北京还出现了胶囊公寓--只有两平米的房间。这样子就满足了大家的不同需求。
同样,在计算机中,内存也不是无限大的,你要计算1+1=2这样的整型数字的加减乘除运算,显然不需要开辟很大的内存空间。而如果要计算1.23456789+2.987654321这样带大量小数的,就需要开辟比较大的空间才能存放的下。于是,计算机的研究者们就考虑,要对数据类型进行分类,分出多种数据类型来适应各种不同的计算条件差异。
例如在C语言中,按照取值的不同,数据类型可以分为两类:
抽象:是指抽取出事物具有的普遍性的本质。他要求抽出问题的特征而忽略非本质的细节,是对具体事物的一个概括。抽象是一种思考问题的方式,它隐藏了繁杂的细节。
抽象数据类型(Abstract Data Type,ADT) 是指一个数据模型及定义在该模型上的一组操作,就相当于高级语言当中类的概念。
抽象数据类型的定义仅取决于它的一组逻辑特性,而与其在计算机内部如何表示和实现无关。
比如1+1=2这样的一个操作,在不同CPU的处理上可能不一样,但由于其定义的数学特性相同,所以在计算机编程者看来,它们都是相同的。
“抽象” 的意义在于数据类型的数学抽象特性。而且,抽象数据类型不仅仅指那些已经定义并实现的数据类型,还可以是计算机编程者在设计软件程序时自己定义的数据类型(类等)。
例如一个3D游戏中,要定位角色的位置,那么总会出现x,y,z三个整型数据组合在一起的坐标。我们就可以定义一个point的抽象数据类型,他拥有x,y,z三个整型变量,这样我们就可以方便的对一个角色的位置进行操作。

描述抽象数据类型的标准格式:
ADT 抽象数据类型
Data
数据元素之间逻辑关系的定义
Operation
操作
endADT
所谓抽象数据类型就是把数据类型和相关操作捆绑在一起。
线性表的抽象数据类型定义:
ADT 线性表(List)
Data
线性表的数据对象集合为{$a_1$,$a_2$,...,$a_n$},每个元素的类型均为DataType。其中,除第一个元素$a_1$外,每个元素有且只有一个直接前驱元素,除了最后一个元素$a_n$外,每一个元素有且只有一个直接后继元素。数据元素之间的关系是一对一的关系。
Operation
InitList(*L):初始化操作,建立一个空的线性表L.
ListEmpty(L):判断线性表是否为空表,若线性表为空表,返回true,否则返回false
ClearList(*L):将线性表清空。
GetElem(L,i,*e):将线性表L中的第i个位置的元素返回给e。
LocateElem(L,e):在线性表L中查找与给定值e相等的元素,如果查找成功,返回该元素在表中序号表示成功;否则,返回0表示失败。
ListInsert(*L,i,e):在线性表L中第i个位置插入新元素e。
ListDelete(*L,i,*e):删除线性表L中第i个位置元素,并用e返回其值。
ListLength(L):返回线性表L的元素个数。
endADT
实现两个线性表A、B的并集操作,即要使得集合 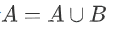
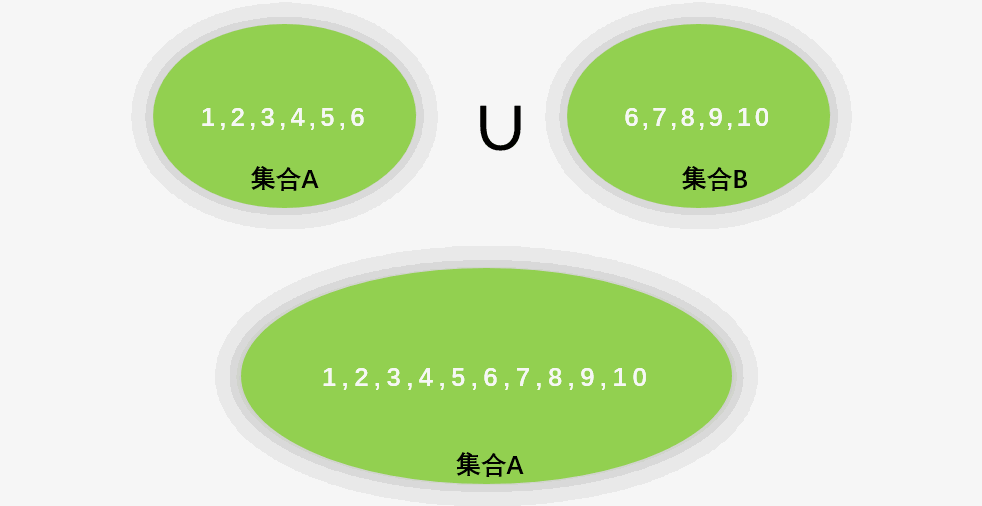
其实仔细思考一下,我们只需要循环遍历集合B中的每一个元素,判断当前元素是否在A中存在,若不存在,则插入A中即可。
综合分析,我们需要运用几个基本的操作组合即可:
参考代码实现:
//union.c
void unionL(List *La, list Lb)
{
int La_len, Lb_len, i;
ElemType e;
La_len=ListLength(*La);
Lb_len=ListLength(Lb);
for( i=1; i <= Lb_len; i++)
{
GetElem(Lb, i, &e);
if( !LocateElem(*La, e)){
ListInsert(La, ++La_len, e);
}
}
}
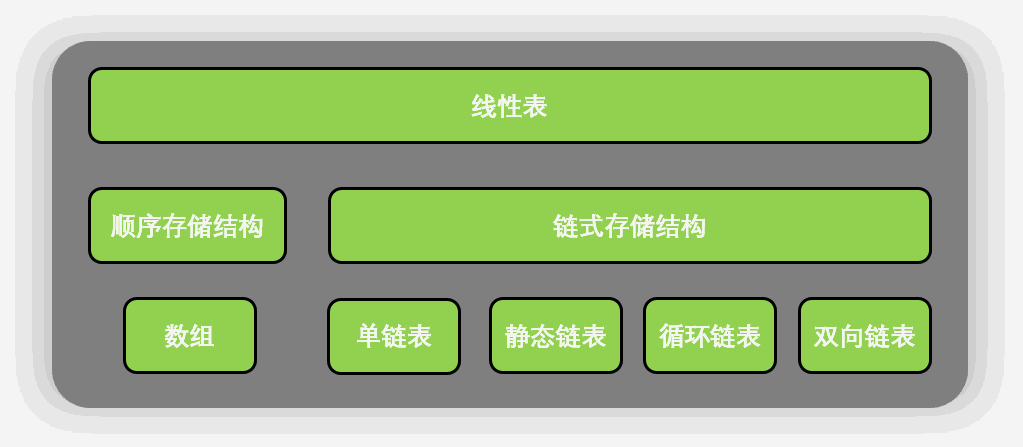
线性表有两种物理存储结构:顺序存储结构和链式存储结构。
线性表的顺序存储结构,指的是用一段地址连续的存储单元依次存储线性表的数据元素。

物理上的存储方式事实上就是在内存中找个初始地址,然后通过占位的形式,把一定的内存空间给占了,然后把相同数据类型的数据元素依次放在这块空地中。
线性表的顺序存储结构的结构代码:
#define MAXSIZE 20
typedef int ElemType;
typedef struct
{
ElemType data[MAXSIZE];
int length;
} SqList;
总结,顺序存储结构封装需要的三个属性:
注意,数组的长度和线性表的当前长度需要区分一下:数组长度是存放线性表的存储空间的总长度,一般初始化后不变。而线性表的当前长度是线性表中元素的个数,是会变化的。
习惯上数组是从0开始的计算方法
假设ElemType占用的是c个存储单元(字节),那么线性表中第i+1个数据元素和第i个数据元素的存储位置的关系是(LOC表示获得存储位置的函数):
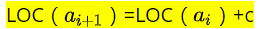
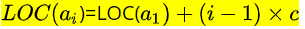
//getElem.c
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;
Status GetElem(SqList L, int i, ElemType *e)
{
if( L.length==0 || i<1 || i>L.length )
{
return ERROR;
}
*e = L.data[i-1];
return OK;
}
Status ListInsert(SqList *L, int i, ElemType e)
{
int k;
if( L->length == MAXSIZE )
{
return ERROR;
}
if ( i<1 || i>L->Length+1)
{
return ERROR;
}
if( i <= L->Length ) {
for( k=L->Length-1; k >= i-1; k-- ){
L->data[k+1] = L->data[k];
}
}
L->data[i-1] = e;
L->Length++;
return OK;
}
** **
删除操作
Status ListDelete(SqList *L, int i, ElemType *e) {
int k;
if( L->length == 0){
return ERROR;
}
if( i < 1 || i > L->length){
return ERROR;
}
*e = L->data[i-1]; //e用于保存第i个位置的值,并返回
if( i < L->Length){
for( k=i; k < L->length; k++){
L->data[k-1]=L->data[k];
}
}
L->length--;
return OK;
}
插入和删除的时间复杂度:
最好的情况:插入和删除操作刚好要求在最后一个位置操作,因为不需要移动任何元素,所以此时的时间复杂度为O(1)
最坏的情况: 如果插入和删除的位置是第一个元素,那就意味着要移动所有的元素向后或者向前,所以这个时间复杂度为O(n)
平均情况: 去取中值
线性表顺序存储结构的优缺点
内存碎片:


来源 | 景禹
作者 | 景禹
版权声明:本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单进行举报,一经查实,本社区将立刻删除涉嫌侵权内容。