K-Means聚类和主成分分析
K-Means聚类和主成分分析
K-Means聚类和主成分分析（PCA），K-Means和PCA都是无监督学习技术的例子，无监督学习问题没有为我们提供任何标签或者目标去学习做出预测，所以无监督算法试图从数据本身中学习一些有趣的结构，我们将首先实现k-means，并了解如何使用它来压缩图像。我们还将用PCA进行实验，以发现面部图像的低维度表示。
写回答
-
K-Means聚类
首先，我们在一个简单的二维数据集上实现并应用k-means，以了解它如何工作。k-means是一种迭代的、无监督的聚类算法，它将类似的实例组合成集群。该算法通过猜测每个集群的初始centroid，反复向最近的集群分配实例，并重新计算该集群的centroid。首先我们要实现一个函数，它为数据中的每个实例找到最接近的centroid。import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sb from scipy.io import loadmat %matplotlib inline def find_closest_centroids(X, centroids): m = X.shape[0] k = centroids.shape[0] idx = np.zeros(m) for i in range(m): min_dist = 1000000 for j in range(k): dist = np.sum((X[i,:] - centroids[j,:]) ** 2) if dist < min_dist: min_dist = dist idx[i] = j return idx测试函数确保它像预期的那样工作，我们使用练习中的测试案例。
data = loadmat('data/ex7data2.mat') X = data['X'] initial_centroids = initial_centroids = np.array([[3, 3], [6, 2], [8, 5]]) idx = find_closest_centroids(X, initial_centroids) idx[0:3]array([0., 2., 1.])输出与文本中的预期值相匹配(我们的数组是zero-indexed而不是one-indexed，所以值比练习中的值要低1)。接下来，我们需要一个函数来计算集群的centroid。centroid是当前分配给集群的所有例子的平均值。
def compute_centroids(X, idx, k): m, n = X.shape centroids = np.zeros((k, n)) for i in range(k): indices = np.where(idx == i) centroids[i,:] = (np.sum(X[indices,:], axis=1) / len(indices[0])).ravel() return centroids compute_centroids(X, idx, 3)array([[ 2.42830111, 3.15792418], [ 5.81350331, 2.63365645], [ 7.11938687, 3.6166844 ]])此输出也与该练习的预期值相匹配。目前为止一切都很顺利。下一部分涉及到实际运行算法的迭代次数和可视化结果。我们在练习中实现了这一步骤，它没有那么复杂，我将从头开始构建它。为了运行这个算法，我们只需要在分配到最近集群的示例和重新计算集群的centroids之间进行交替操作。
def run_k_means(X, initial_centroids, max_iters): m, n = X.shape k = initial_centroids.shape[0] idx = np.zeros(m) centroids = initial_centroids for i in range(max_iters): idx = find_closest_centroids(X, centroids) centroids = compute_centroids(X, idx, k) return idx, centroids idx, centroids = run_k_means(X, initial_centroids, 10)我们现在可以使用颜色编码表示集群成员。
cluster1 = X[np.where(idx == 0)[0],:] cluster2 = X[np.where(idx == 1)[0],:] cluster3 = X[np.where(idx == 2)[0],:] fig, ax = plt.subplots(figsize=(12,8)) ax.scatter(cluster1[:,0], cluster1[:,1], s=30, color='r', label='Cluster 1') ax.scatter(cluster2[:,0], cluster2[:,1], s=30, color='g', label='Cluster 2') ax.scatter(cluster3[:,0], cluster3[:,1], s=30, color='b', label='Cluster 3') ax.legend()
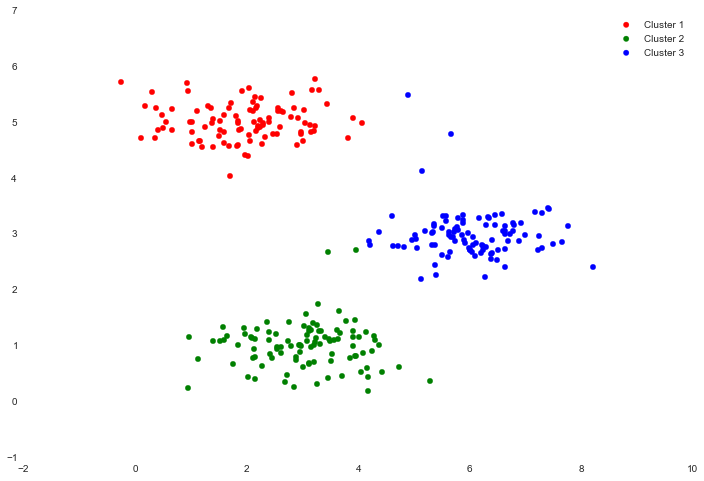
我们跳过了初始化centroid的过程。这可能会影响算法的收敛性。
接下来创建一个可以选择随机例子的函数，并将这些例子作为初始的centroid。
def init_centroids(X, k): m, n = X.shape centroids = np.zeros((k, n)) idx = np.random.randint(0, m, k) for i in range(k): centroids[i,:] = X[idx[i],:] return centroids init_centroids(X, 3)array([[ 1.15354031, 4.67866717], [ 6.27376271, 2.24256036], [ 2.20960296, 4.91469264]])我们的下一任务是应用K-means实现图像压缩。我们可以使用集群来查找图像中最具有代表性的少量的颜色，并使用集群分配将原来的24位颜色映射到一个低维度的颜色空间。这是我们要压缩的图像。
原始像素数据已经预加载了，把它输入进来。
image_data= loadmat('data/bird_small.mat') image_data{'A': array([[[219, 180, 103], [230, 185, 116], [226, 186, 110], ..., [ 14, 15, 13], [ 13, 15, 12], [ 12, 14, 12]], ..., [[ 15, 19, 19], [ 20, 20, 18], [ 18, 19, 17], ..., [ 65, 43, 39], [ 58, 37, 38], [ 52, 39, 34]]], dtype=uint8), '__globals__': [], '__header__': 'MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Tue Jun 5 04:06:24 2012', '__version__': '1.0'}我们可以快速查看数据的形状，以验证它是否像我们预期的图像。
A= image_data['A'] A.shape(128L,128L,3L)现在我们需要对数据进行预处理，并将它输入到k-means算法中。
# normalize value ranges A = A / 255. # reshape the array X = np.reshape(A, (A.shape[0] * A.shape[1], A.shape[2])) # randomly initialize the centroids initial_centroids = init_centroids(X, 16) # run the algorithm idx, centroids = run_k_means(X, initial_centroids, 10) # get the closest centroids one last time idx = find_closest_centroids(X, centroids) # map each pixel to the centroid value X_recovered = centroids[idx.astype(int),:] # reshape to the original dimensions X_recovered = np.reshape(X_recovered, (A.shape[0], A.shape[1], A.shape[2])) plt.imshow(X_recovered)
我们在压缩中创建了一些artifact，尽管将原始图像映射到仅16种颜色，但图像的主要特征仍然存在。这是关于k-means的部分，接下来我们来看关于主成分分析的部分。
主成分分析
PCA是一个可以在数据集中找到“主成分”或者最大方差方向的线性变换。它可以用于其他事物的维度减少。在这个练习中，我们需要实现PCA，并将其应用于一个简单的二维数据集，观察它是如何工作的。从加载和可视化数据集开始。data = loadmat('data/ex7data1.mat') X = data['X'] fig, ax = plt.subplots(figsize=(12,8)) ax.scatter(X[:, 0], X[:, 1])
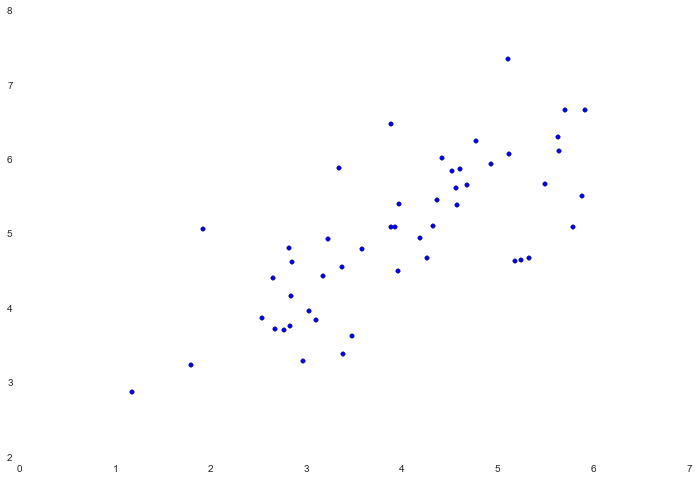
PCA的算法相当简单。在保证数据正规化后，输出只是原始数据协方差矩阵的单值分解。由于numpy已经有内置函数来计算矩阵协方差和SVD，我们将利用这些函数而不是从头开始。def pca(X): # normalize the features X = (X - X.mean()) / X.std() # compute the covariance matrix X = np.matrix(X) cov = (X.T * X) / X.shape[0] # perform SVD U, S, V = np.linalg.svd(cov) return U, S, V U, S, V = pca(X) U, S, V(matrix([[-0.79241747, -0.60997914], [-0.60997914, 0.79241747]]), array([ 1.43584536, 0.56415464]), matrix([[-0.79241747, -0.60997914], [-0.60997914, 0.79241747]]))现在我们已经有了主成分（矩阵U），我们可以利用它把原始数据投入到一个更低维度的空间，对于这个任务，我们将实现一个函数，它计算投影并只选择顶部K成分，有效地减少了维度的数量。
def project_data(X, U, k): U_reduced = U[:,:k] return np.dot(X, U_reduced) Z = project_data(X, U, 1) Zmatrix([[-4.74689738], [-7.15889408], [-4.79563345], [-4.45754509], [-4.80263579], ..., [-6.44590096], [-2.69118076], [-4.61386195], [-5.88236227], [-7.76732508]])我们也可以通过改变采取的步骤来恢复原始数据。
def recover_data(Z, U, k): U_reduced = U[:,:k] return np.dot(Z, U_reduced.T) X_recovered = recover_data(Z, U, 1) X_recoveredmatrix([[ 3.76152442, 2.89550838], [ 5.67283275, 4.36677606], [ 3.80014373, 2.92523637], [ 3.53223661, 2.71900952], [ 3.80569251, 2.92950765], ..., [ 5.10784454, 3.93186513], [ 2.13253865, 1.64156413], [ 3.65610482, 2.81435955], [ 4.66128664, 3.58811828], [ 6.1549641 , 4.73790627]])如果我们尝试去可视化恢复的数据，会很容易的发现算法的工作原理。
fig, ax= plt.subplots(figsize=(12,8)) ax.scatter(X_recovered[:,0], X_recovered[:,1])
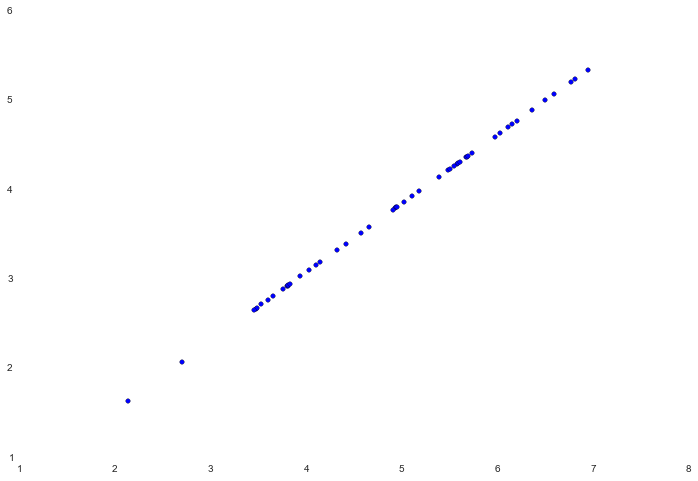
注意这些点如何被压缩成一条虚线。虚线本质上是第一个主成分。当我们将数据减少到一个维度时，我们切断的第二个主成分可以被认为是与这条虚线的正交变化。由于我们失去了这些信息，我们的重建只能将这些点与第一个主成分相关联。我们这次练习的最后一项任务是将PCA应用于脸部图像。通过使用相同降维技术，我们可以使用比原始图像少得多的数据来捕捉图像的“本质”。
faces= loadmat('data/ex7faces.mat') X= faces['X'] X.shape(5000L,1024L)该练习代码包含一个函数，它将在网格中的数据集中渲染前100个脸部图像。你可以在练习文本中找到它们，不需要重新生成。
face= np.reshape(X[3,:], (32,32)) plt.imshow(face)
只有32 x 32灰度图像。下一步我们要在脸部图像数据集上运行PCA，并取得前100个主成分。U, S, V= pca(X) Z= project_data(X, U,100)现在尝试恢复原来的结构并重新渲染它。
X_recovered= recover_data(Z, U,100) face= np.reshape(X_recovered[3,:], (32,32)) plt.imshow(face)
结果并没有像预期的维度数量减少10倍，可能是因为我们丢失了一些细节部分。2019-11-27 17:42:30赞同 1 展开评论 打赏
版权声明：本文内容由阿里云实名注册用户自发贡献，版权归原作者所有，阿里云开发者社区不拥有其著作权，亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容，填写侵权投诉表单进行举报，一经查实，本社区将立刻删除涉嫌侵权内容。
