softmax函数的数学推导及Python实现

softmax用于多分类过程中最后一层，将多个神经元的输出，映射到（0, 1）区间内，可以看成概率来理解，从而来进行多分类！

softmax函数如下：

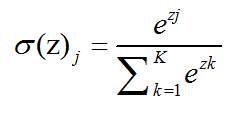
更形象的如下图表示：
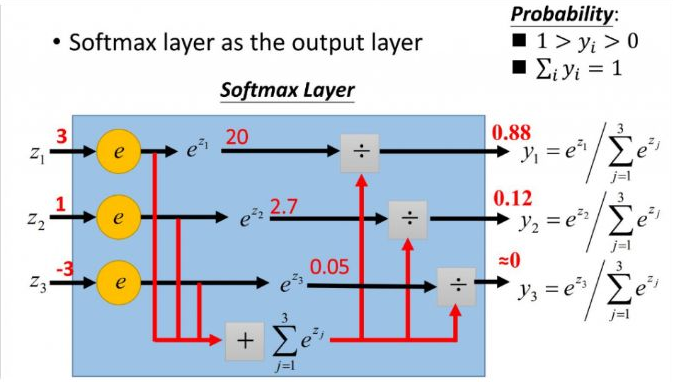softmax 直白来说就是讲原来输出是 3, 1, -3 通过 softmax 函数一作用，就映射成为（0， 1）的值，而这些值的累和为1，那么我们就可以将其理解成概率，在最后选取输出节点的时候，我们可以选取概率最大的节点，作为我们的预测目标！

Python代码实现：

# _*_coding:utf-8_*_
import tensorflow as tf
import numpy as np
import math
 
 
# softmax函数，或称归一化指数函数
def softmax(x, axis=1):
    # 为了避免求 exp(x) 出现溢出的情况，一般需要减去最大值
    # 计算每行的最大值
    row_max = x.max(axis=axis)
    # 每行元素都需要减去对应的最大值，否则求exp(x)会溢出，导致INF情况
    row_max = row_max.reshpae(-1, 1)
    x = x - row_max
 
    x_exp = np.exp(x)
    # 如果是列向量，则axis=0
    x_sum = np.sum(x_exp, axis=1, keepdims=True)
    s = x_exp / x_sum
    return s
 
# 简单一些
def softmax(x):
    """Compute softmax values for each sets of scores in x."""
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum()
 
# 使用 tf的softmax函数
with tf.Session() as sess:
    tf_s2 = tf.nn.softmax(x, axis=axis)
    s2 = sess.run(tf_s2)

　　下面我们分析一下，减去最大值和不减去最大值是否有必要吗？首先看代码：

import numpy as np
 
def softmax(x):
    """Compute softmax values for each sets of scores in x."""
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum()
 
def softmax1(x):
    """Compute softmax values for each sets of scores in x."""
    return np.exp(x) / np.sum(np.exp(x), axis=0)
 
scores = [3.0, 1.0, 0.2]
print(softmax(scores))
print(softmax1(scores))
'''
结果输出如下：
[0.8360188  0.11314284 0.05083836]
[0.8360188  0.11314284 0.05083836]
'''

其实两个结果输出是一样的，即使第一个实现了每列和最大值的差异，然后除以总和，但是问题来了，实现在代码和时间复杂度方面是否相似？哪一个更有效率？
当然，他们都是正确的，但是从数值稳定性的角度来看，第一个是正确的，因为我们避免了求 exp(x) 出现溢出的情况，这里减去了最大值。我们推导一下：

# 转化公式： a ^(b – c)=(a ^ b)/(a ^ c)
 
e ^ (x - max(x)) / sum(e^(x - max(x))
 
= e ^ x / (e ^ max(x) * sum(e ^ x / e ^ max(x)))
 
= e ^ x / sum(e ^ x)