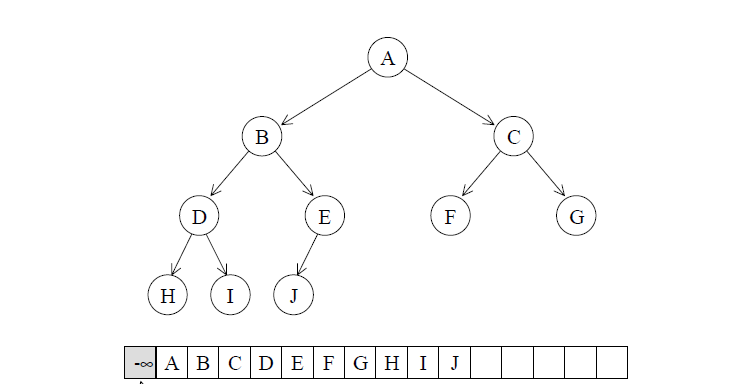
binary heap 是一种 Complete binary tree, 也就是,整棵 binary tree 除叶子节点之外,是填满的,而最底层的叶节点由左至右又不得有空隙。
heap 的实现
假设动用 一 个小技巧 3 ,将 array 的 #0 元素保留(或设为无限大值或无限小值),那么当 complete binary tree 中 的某个节点位 于 array 的i 处,其左子节点必位于 array 的2i 处,其右子节点必位于 array 的2i+1 处,其父节点必位于「i/2 」处 (此处的「」权且代表高斯符号,取其整数)。通过这么简单的位置规则,array 可以轻易实作出 complete binary tree 。这种以array 表述 tree 的方式,我们称为隐式表述法(implicit representation )。
注意: STL 中并未使用此技巧,此点需要特别注意,后面的所有的下标都与此有关。
heap 的分类
根据元素排列方式, heap 可分为 max-heap 和min-heap 两种,前者每个节点的键值( key )都大于或等于其子节点键值,后者的每个节点键值( key )都小于或等于其子节点键值。因此, max-heap 的最大值在根节点,并总是位于底层 array 或 vector 的 起 头 处 ; min-heap 的 最 小 值 在 根 节 点 , 亦 总 是 位 于 底 层 array 或 vector 的起头处。
注意: STL 提供的是 max-heap
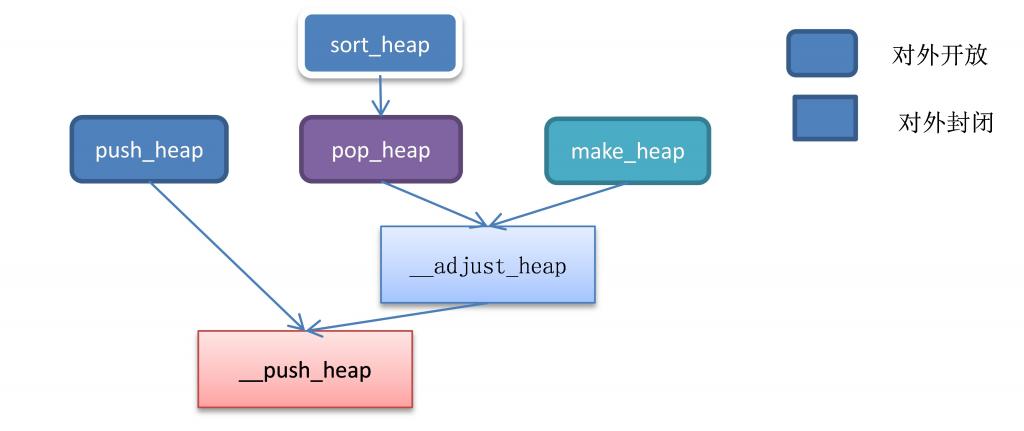
heap 算法依赖关系
push_heap 算法
为了满足 complete binary tree 的条件,新加入的元素 ㆒ 定要放在最 下一 层做为叶节点,并填补在由左至右的第 一 个空格,也就是把新元素安插在底层 vector 的 end() 处。新元素是否适合于其现有位置呢?为满足 max-heap 的条件(每个节点的键值都大于或等于其子节点键值),我们执行 一 个所谓的 percolate up ( 上 溯)程序:将新节点拿来与其父节点比较,如果其键值( key )比父节点大,就父子对换位置。如此 一 直 上 溯,直到不需对换或直到根节点为止。
//first: 底层容器的起始位置 iterator //holeIndex: 新值将被置于的位置 //topIndex: 根节点在容器中的索引 //value: 新值的值 template <class RandomAccessIterator, class Distance, class T> void __push_heap (RandomAccessIterator first, Distance holeIndex, Distance topIndex, T value) { Distance parent = (holeIndex - 1) / 2; // 找出父节点 while (holeIndex > topIndex && *(first + parent) < value) { // 当尚未到达顶端,且父节点小于新值(于是不符合 heap 的次序特性) // 由于以 上 使用 operator< ,可知 STL heap 是 ㆒ 种 max-heap (大者为父)。 *(first + holeIndex) = *(first + parent); // 令洞值为父值 holeIndex = parent; // percolate up :调整洞号,向 上 提升至父节点。 parent = (holeIndex - 1) / 2; // 新洞的父节点 } // 持续至顶端,或满足 heap 的次序特性为止。 *(first + holeIndex) = value; // 令洞值为新值,完成安插动作。 }
pop_heap 算法
pop 动作取走根节点(其实是移至底部容器 vector 的最后一个元素)之后,为了满足 complete binary tree 的条件,必须割舍最下层最右边的叶节点,并将其值安插至 max_heap (安插时用到 __push_heap )。(取走根节点后)为满足 max-heap 的条件(每个节点的键值都大于或等于其子节点键值),我们执行一个所谓的 percolate down (下溯)程序:将根节点取走(最大值被取走后,形成一个「 hole 」),然后比较其两个子节点键值( key ),并与较大子节点对调位置。如此一直下放,直到这个「 hole 」的键值大于左右两个子节点,或直到下放至叶节点为止。
//first: 底层容器的起始位置 iterator //holeIndex: 被取走的根植形成 hole 位置的索引 //len: 指定了排序的区域大小 //value: 割舍之叶节点之值 template <class RandomAccessIterator, class Distance, class T> void __adjust_heap (RandomAccessIterator first, Distance holeIndex, Distance len, T value) { Distance topIndex = holeIndex; Distance secondChild = 2 * holeIndex + 2; // 洞节点之右子节点 // 注意以下的比较,仅仅是左右子节点的比较,并且以两者较大者填充 hole ,然后查找新的 hole ,直至将 hole 下放到 // 叶节点。如果在此过程中割舍点的值同时大于左右两个节点,则不满足 max_heap ,这是最后需要执行一次 //__push_heap 的原因所在,所以 __push_heap 必不可少 while (secondChild < len) { // 比较洞节点之左右两个子值,然后以 secondChild 代表较大子节点。 if (*(first + secondChild) < *(first + (secondChild - 1))) secondChild--; // Percolate down :令较大子值为洞值,再令洞号 下 移至较大子节点处。 *(first + holeIndex) = *(first + secondChild); holeIndex = secondChild; // 找出新洞节点的右子节点 secondChild = 2 * (secondChild + 1); } if (secondChild == len) { // 没有右子节点,只有左子节点 // Percolate down :令左子值为洞值,再令洞号 下 移至左子节点处。 *(first + holeIndex) = *(first + (secondChild - 1)); holeIndex = secondChild - 1; } __push_heap (first, holeIndex, topIndex, value); }
sort_heap 算法
既然每次 pop_heap 可获得 heap 之 中 键值最大的元素,如果持续对整个 heap 做pop_heap 动作,每次将操作范围从后向前缩减 一 个元素(因为 pop_heap 会把键值最大的元素放在底部容器的最尾端),当整个程序执行完毕,我们便有了㆒个递增序列。
template <class RandomAccessIterator> void sort_heap (RandomAccessIterator first, RandomAccessIterator last) { // 以 下 ,每执行 一 次 pop_heap() ,极值(在 STL heap 中 为极大值)即被放在尾端。 // 扣除尾端再执行 一 次 pop_heap() ,次极值又被放在新尾端。 一 直 下 去,最后即得 // 排序结果。 while (last - first > 1) pop_heap (first, last--); // 每执行 pop_heap() 一 次,操作范围即退缩 一 格。 }
make_heap 算法
这个算法用来将一段现有的数据转化为一个heap 。其主要依据就是 complete binary tree 的隐式表述( implicit representation )。
template <class RandomAccessIterator, class T, class Distance> void __make_heap (RandomAccessIterator first, RandomAccessIterator last, T*, Distance*) { if (last - first < 2) return; // 如果长度为 0 或 1 ,不必重新排列。 Distance len = last - first; // 找出第一个需要重排的子树头部,以 parent 标示出。由于任何叶节点都不需执行 // perlocate down ,所以有以下计算。 parent 命名不佳,名为 holeIndex 更好。 Distance parent = (len - 2)/2; while (true) { // 重排以 parent 为首的子树。 len 是为了让 __adjust_heap() 判断操作范围 // 再次分析一下 __adjust_heap 的作用:每次 while 循环 确保且仅仅确保 了 first 到 parent 之间的数据满足 heap 。 //__adjust_heap 下溯的 while 循环确保了其下溯路线上的节点都大于和其共父节点的节点, //__adjust_heap 上溯的 __push_heap 确保了上述下溯路线上节点父节点大于子节点 // 综上所诉, __adjust_heap 确保了且仅仅确保了 first 到 parent 之间的数据满足 heap 。 __adjust_heap (first, parent, len, T(*(first + parent))); if (parent == 0) return; parent--; // 走完根节点,就结束。 // (即将重排之子树的)头部向前一个节点 } }
本文作者 : cyningsun
本文地址 : https://www.cyningsun.com/04-04-2011/stl-heap.html
版权声明 :本博客所有文章除特别声明外,均采用 CC BY-NC-ND 3.0 CN 许可协议。转载请注明出处!