题目概述(简单难度)
给定一个二叉树,检查它是否是镜像对称的。
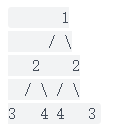
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1 / \ 2 2 / \ / \ 3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1 / \ 2 2 \ \ 3 3
题目链接:
思路与代码
思路展现
这道题目的思路也是非常简单的:
对称二叉树前两层的比较都是一样的,当到了第三层的时候,比较的是左子树的左节点和右子树的右节点是否相同,如下图所示:
代码示例
class Solution { public boolean isSameTree(TreeNode p, TreeNode q) { if(p == null && q != null || p !=null && q == null) { return false; } if(p == null && q == null) { return true; } if(p.val != q.val) { return false; } //return这里发生变化 return isSameTree(p.left,q.right) && isSameTree(p.right,q.left); } public boolean isSymmetric(TreeNode root) { if(root == null) { return true; } if(isSameTree(root.left,root.right)) { return true; } return false; } }
总结
考察对于二叉树的掌握,也是入门的经典题目
时间复杂度:O(n),这里属于同步遍历左右两棵互为镜像的子树,所以时间复杂度为O(n)
空间复杂度:这里的空间复杂度和递归使用的栈空间有关,而栈空间与二叉树的深度有关,这里两棵互为镜像的左右子树的深度都是相等的,假设都为n,所以这里递归层数不超过 n,故渐进空间复杂度为 O(n).