KD-tree 原理
kd树(k-dimensional树的简称),是一种分割k维数据空间的数据结构。主要应用于多维空间关键数据的搜索(如:范围搜索和最近邻搜索)。
其实KDTree就是二叉搜索树的变种。这里的K = 3.
Kd-tree的原理是这样的:不比较全部的k维数据,而是选择其中某一个维度比较,根据这个维度进行空间划分。
只需要判断出在哪一个维度比较 然后判断以哪个数据条目分依据划分。 就可以构造一个KD tree了
确定划分维度:这里维度的确定需要注意的是尽量要使得这个维度上所有数据项数值的分布尽可能地有大方差,也就是说,数据在这个维度上尽可能分散。这就好比是我们切东西,如果你切的是一根黄瓜,当让横着切要比竖着切更容易。所以我们应该先对所有维度的数值计算方差,选择方差最大的那个维度;
选择充当切割标准的数据项:那么只需要求得这个维度上所有数值的中位数即可;
快速邻域搜索
求一个点的最紧邻点
在pcl中可以通过对点云建立 kdtree ,然后求一个点的 最紧邻点

需要包含的头文件 注意里面一个头文件 必须按这种 路径
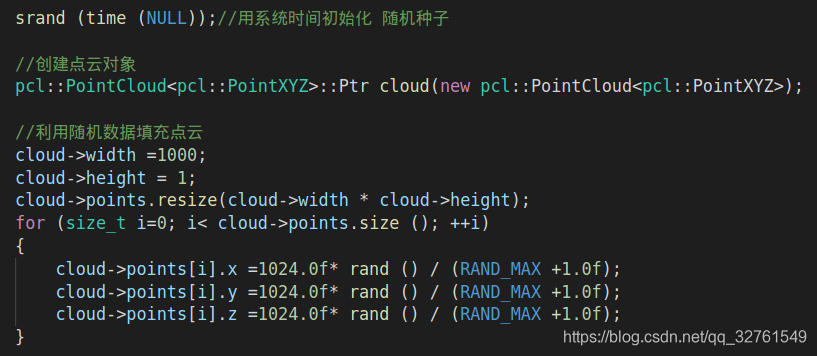
循环构建 一个 1000个点 的 点云

创建KdTreeFLANN 对象
这个就是 一个空的 kdtree 模型 , 之后 将点云 输入进去 就可以了 。

将随机生成的 1000个点的点云,输入到 kdtree ,这样就构建好了。
操作还是很简单的。不需要知道如何构建的。原理就在上面。

创建一个查询点 同样分配随机坐标

创建两个向量 存储搜索到的k紧邻 一个存点的索引 一个存点的距离平方

终端输出 相关 信息
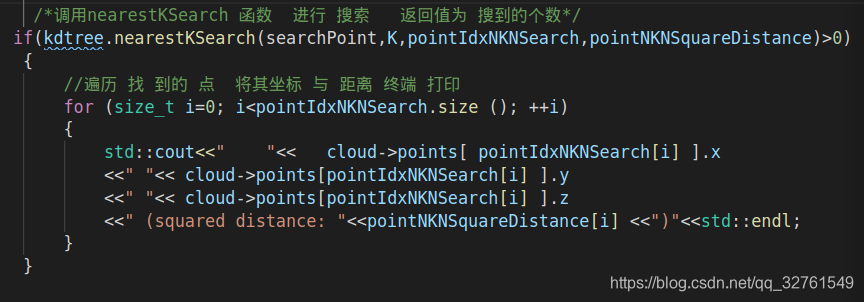
调用nearestKSearch 函数 进行 搜索 返回值为 搜到的个数
遍历 找 到的 点 将其坐标 与 距离 终端 打印
这里要重点说下 nearestKSearch 函数 这个是 查询点最近邻的核心函数
通过构建好的ketree 调用。然后参数
- 要查询的点
- 查询返回的个数
- 查询到的点的索引存放向量
- 查询到的点的距离平方存放向量
这个函数的返回值 是 查询到的个数。
Code
#include <pcl/point_cloud.h>
//其它资料给的 是 #include <pcl/kdtree/kdtree_flann.h> 也有这个文件 但是会报错
#include <pcl/kdtree/impl/kdtree_flann.hpp>
#include <iostream>
#include <vector>
#include <ctime>
int main(int argc, char**argv)
{
srand (time (NULL));//用系统时间初始化 随机种子
//创建点云对象
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
//利用随机数据填充点云
cloud->width =1000;
cloud->height = 1;
cloud->points.resize(cloud->width * cloud->height);
for (size_t i=0; i< cloud->points.size (); ++i)
{
cloud->points[i].x =1024.0f* rand () / (RAND_MAX +1.0f);
cloud->points[i].y =1024.0f* rand () / (RAND_MAX +1.0f);
cloud->points[i].z =1024.0f* rand () / (RAND_MAX +1.0f);
}
/*创建KdTreeFLANN 对象*/
pcl::KdTreeFLANN<pcl::PointXYZ> kdtree;
/*把上面建立的点云 设置为 KDTREE的输入*/
kdtree.setInputCloud(cloud);
//创建一个查询点 同样分配随机坐标
pcl::PointXYZ searchPoint;
searchPoint.x=1024.0f* rand () / (RAND_MAX +1.0f);
searchPoint.y=1024.0f* rand () / (RAND_MAX +1.0f);
searchPoint.z=1024.0f* rand () / (RAND_MAX +1.0f);
//创建两个向量 存储搜索到的k紧邻 一个存点的索引 一个存点的距离平方
int K = 10;
std::vector<int> pointIdxNKNSearch(K);
std::vector<float> pointNKNSquareDistance(K);
//终端输出 相关 信息
std::cout<<"K nearest neighbor search at ("<<searchPoint.x
<<" "<<searchPoint.y
<<" "<<searchPoint.z
<<") with K="<< K <<std::endl;
/*调用nearestKSearch 函数 进行 搜索 返回值为 搜到的个数*/
if(kdtree.nearestKSearch(searchPoint,K,pointIdxNKNSearch,pointNKNSquareDistance)>0)
{
//遍历 找 到的 点 将其坐标 与 距离 终端 打印
for (size_t i=0; i<pointIdxNKNSearch.size (); ++i)
{
std::cout<<" "<< cloud->points[ pointIdxNKNSearch[i] ].x
<<" "<< cloud->points[pointIdxNKNSearch[i] ].y
<<" "<< cloud->points[pointIdxNKNSearch[i] ].z
<<" (squared distance: "<<pointNKNSquareDistance[i] <<")"<<std::endl;
}
}
return 0;
}Result

求一个半径内的最紧邻点
还有上面的工程的基础,生成随机的1000个点云,建立kdtree。
建立搜索点

创建两个向量 存储搜索到的近邻邻 一个存点的索引 一个存点的距离平方

创建一个随机半径

打印搜索点和半径 的 信息
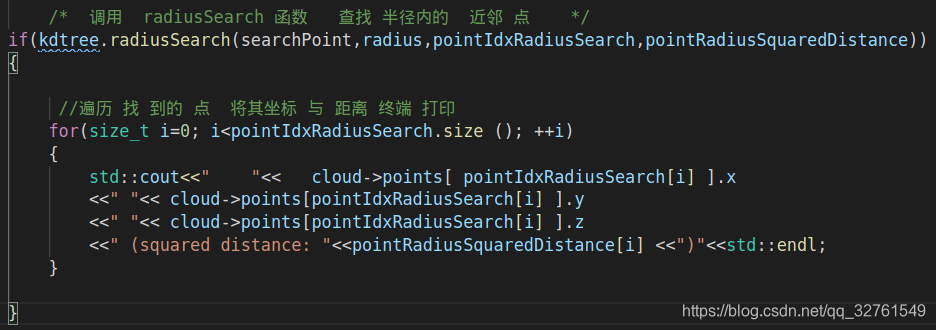
调用 radiusSearch 函数 查找 半径内的 近邻 点
遍历 找 到的 点 将其坐标 与 距离 终端 打印
这里要重点说下 radiusSearch 函数 这个是 查询点半径内最近邻的核心函数
通过构建好的ketree 调用。然后参数
- 要查询的点
- 查询的半径范围
- 查询到的点的索引存放向量
- 查询到的点的距离平方存放向量
这个函数的返回值 是 查询到的个数。
Code
//创建两个向量 存储搜索到的近邻邻 一个存点的索引 一个存点的距离平方
std::vector<int> pointIdxRadiusSearch;
std::vector<float>pointRadiusSquaredDistance;
//创建一个随机半径
float radius = 256.0*rand()/(RAND_MAX+1.0f);
//打印搜索点和半径 的 信息
std::cout<<"Neighbors within radius search at ("<<searchPoint.x
<<" "<<searchPoint.y
<<" "<<searchPoint.z
<<") with radius="<< radius <<std::endl;
/* 调用 radiusSearch 函数 查找 半径内的 近邻 点 */
if(kdtree.radiusSearch(searchPoint,radius,pointIdxRadiusSearch,pointRadiusSquaredDistance)>0)
{
//遍历 找 到的 点 将其坐标 与 距离 终端 打印
for(size_t i=0; i<pointIdxRadiusSearch.size (); ++i)
{
std::cout<<" "<< cloud->points[ pointIdxRadiusSearch[i] ].x
<<" "<< cloud->points[pointIdxRadiusSearch[i] ].y
<<" "<< cloud->points[pointIdxRadiusSearch[i] ].z
<<" (squared distance: "<<pointRadiusSquaredDistance[i] <<")"<<std::endl;
}
}Result






