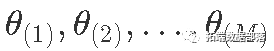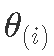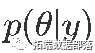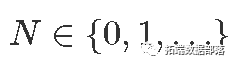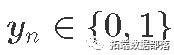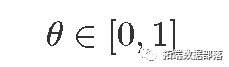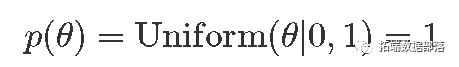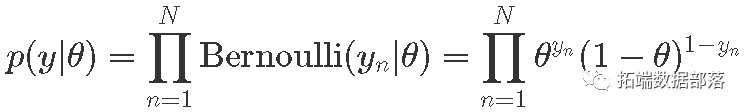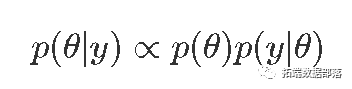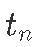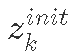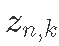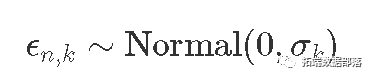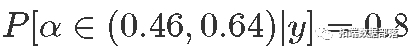原文链接:http://tecdat.cn/?p=19737
Stan是一种用于指定统计模型的概率编程语言。Stan通过马尔可夫链蒙特卡罗方法(例如No-U-Turn采样器,一种汉密尔顿蒙特卡洛采样的自适应形式)为连续变量模型提供了完整的贝叶斯推断。
可以通过R使用rstan 包来调用Stan,也可以 通过Python使用 pystan 包。这两个接口都支持基于采样和基于优化的推断,并带有诊断和后验分析。
在本文中,简要展示了Stan的主要特性。还显示了两个示例:第一个示例与简单的伯努利模型相关,第二个示例与基于常微分方程的Lotka-Volterra模型有关。
什么是Stan?
- Stan是命令式概率编程语言。
- Stan程序定义了概率模型。
- 它声明数据和(受约束的)参数变量。
- 它定义了对数后验。
- Stan推理:使模型拟合数据并做出预测。
- 它可以使用马尔可夫链蒙特卡罗(MCMC)进行完整的贝叶斯推断。
- 使用变分贝叶斯(VB)进行近似贝叶斯推断。
- 最大似然估计(MLE)用于惩罚最大似然估计。
Stan计算什么?
- 得出后验分布 。
- MCMC采样。
- 绘制 ,其中每个绘制 都按后验概率 的边缘分布。
- 使用直方图,核密度估计等进行绘图
点击标题查阅往期内容
01
02
03
04
安装 rstan
要在R中运行Stan,必须安装 rstan C ++编译器。在Windows上, Rtools 是必需的。
最后,安装 rstan:
install.packages(rstan)
Stan中的基本语法
定义模型
Stan模型由六个程序块定义 :
- 数据(_必填_)。
- 转换后的数据。
- 参数(_必填_)。
- 转换后的参数。
- 模型(_必填_)。
- 生成的数量。
数据块读出的外部信息。
data { int N; int x\[N\]; int offset; }
变换后的数据 块允许数据的预处理。
transformed data { int y\[N\]; for (n in 1:N) y\[n\] = x\[n\] - offset; }
参数 块定义了采样的空间。
parameters { real<lower=0> lambda1; real<lower=0> lambda2; }
变换参数 块定义计算后验之前的参数处理。
transformed parameters { real<lower=0> lambda; lambda = lambda1 + lambda2; }
在 模型 块中,我们定义后验分布。
model { y ~ poisson(lambda); lambda1 ~ cauchy(0, 2.5); lambda2 ~ cauchy(0, 2.5); }
最后, 生成的数量 块允许进行后处理。
generated quantities { int x_predict; x\_predict = poisson\_rng(lambda) + offset; }
类型
Stan有两种原始数据类型, 并且两者都是有界的。
- int 是整数类型。
- real 是浮点类型。
int<lower=1> N;real<upper=5> alpha;real<lower=-1,upper=1> beta;real gamma;real<upper=gamma> zeta;
实数扩展到线性代数类型。
vector\[10\] a; // 列向量matrix\[10, 1\] b;row_vector\[10\] c; // 行向量matrix\[1, 10\] d;
整数,实数,向量和矩阵的数组均可用。
real a\[10\]; vector\[10\] b; matrix\[10, 10\] c;
Stan还实现了各种 约束 类型。
simplex\[5\] theta; // sum(theta) = 1ordered\[5\] o; // o\[1\] < ... < o\[5\]positive_ordered\[5\] p;corr_matrix\[5\] C; // 对称和cov_matrix\[5\] Sigma; // 正定的
关于Stan的更多信息
所有典型的判断和循环语句也都可用。
if/then/elsefor (i in 1:I)while (i < I)
有两种修改 后验的方法。
y ~ normal(0, 1);target += normal_lpdf(y | 0, 1);# 新版本的Stan中已弃用:increment\_log\_posterior(log_normal(y, 0, 1))
而且许多采样语句都是 _矢量化的_。
parameters { real mu\[N\]; real<lower=0> sigma\[N\]; }model { // for (n in 1:N) // y\[n\] ~ normal(mu\[n\], sigma\[n\]); y ~ normal(mu, sigma); // 向量化版本}
贝叶斯方法
概率是 认知的。例如, 约翰·斯图亚特·米尔 (_John Stuart Mill)_说:
事件的概率不是事件本身,而是我们或其他人期望发生的情况的程度。每个事件本身都是确定的,不是可能的;如果我们全部了解,我们应该或者肯定地知道它会发生,或者它不会。
对我们来说,概率表示对它发生的期望程度。
概率可以量化不确定性。
Stan的贝叶斯示例:重复试验模型
我们解决一个小例子,其中的目标是给定从伯努利分布中抽取的随机样本,以估计缺失参数的后验分布 (成功的机会)。
步骤1:问题定义
在此示例中,我们将考虑以下结构:
数据:
- ,试用次数。
- ,即试验_n的_结果 (已知的建模数据)。
参数:
- 先验分布
- 概率
- 后验分布
步骤2:Stan
我们创建Stan程序,我们将从R中调用它。
data { int<lower=0> N; // 试验次数 int<lower=0, upper=1> y\[N\]; // 试验成功}model { theta ~ uniform(0, 1); // 先验 y ~ bernoulli(theta); // 似然}
步骤3:数据
在这种情况下,我们将使用示例随机模拟一个随机样本,而不是使用给定的数据集。
# 生成数据y = rbinom(N, 1, 0.3)y ## \[1\] 0 0 0 1 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 根据数据计算 _MLE_作为样本均值: ## \[1\] 0.25
步骤4:rstan使用贝叶斯后验估计
最后一步是使用R中的Stan获得我们的估算值。
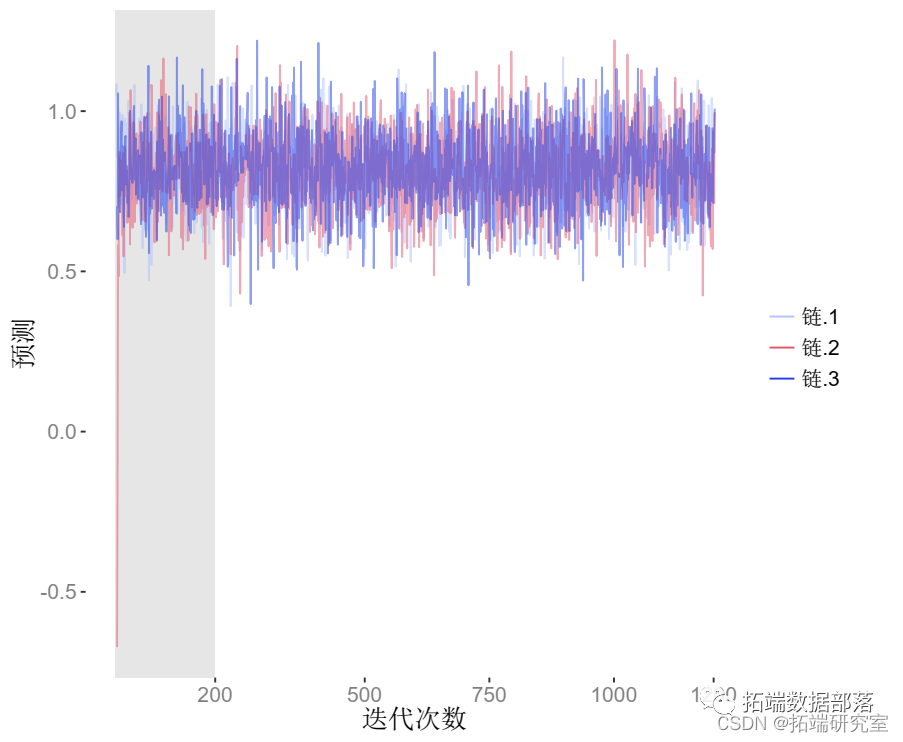
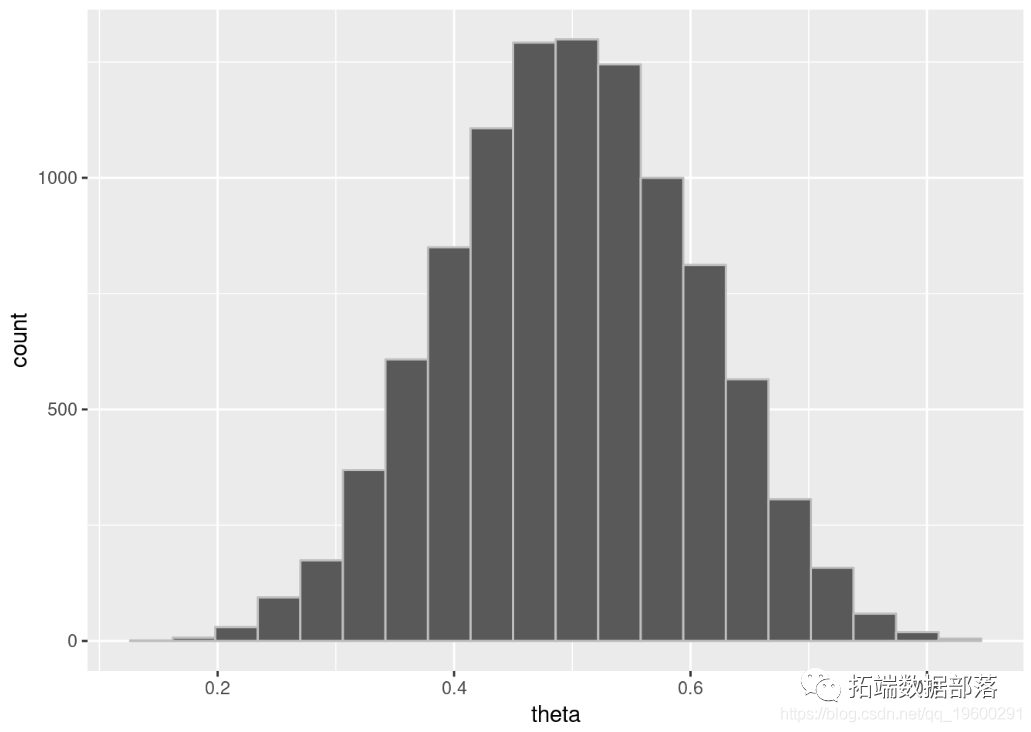
## ## SAMPLING FOR MODEL '6dcfbccbf2f063595ccc9b93f383e221' NOW (CHAIN 1). ## Chain 1: ## Chain 1: Gradient evaluation took 7e-06 seconds ## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.07 seconds. ## Chain 1: Adjust your expectations accordingly! ## Chain 1: ## Chain 1: ## Chain 1: Iteration: 1 / 5000 \[ 0%\] (Warmup) ## Chain 1: Iteration: 500 / 5000 \[ 10%\] (Warmup) ## Chain 1: Iteration: 1000 / 5000 \[ 20%\] (Warmup) ## Chain 1: Iteration: 1500 / 5000 \[ 30%\] (Warmup) ## Chain 1: Iteration: 2000 / 5000 \[ 40%\] (Warmup) ## Chain 1: Iteration: 2500 / 5000 \[ 50%\] (Warmup) ## Chain 1: Iteration: 2501 / 5000 \[ 50%\] (Sampling) ## Chain 1: Iteration: 3000 / 5000 \[ 60%\] (Sampling) ## Chain 1: Iteration: 3500 / 5000 \[ 70%\] (Sampling) ## Chain 1: Iteration: 4000 / 5000 \[ 80%\] (Sampling) ## Chain 1: Iteration: 4500 / 5000 \[ 90%\] (Sampling) ## Chain 1: Iteration: 5000 / 5000 \[100%\] (Sampling) ## Chain 1: ## Chain 1: Elapsed Time: 0.012914 seconds (Warm-up) ## Chain 1: 0.013376 seconds (Sampling) ## Chain 1: 0.02629 seconds (Total) ## Chain 1: ... ## SAMPLING FOR MODEL '6dcfbccbf2f063595ccc9b93f383e221' NOW (CHAIN 4). ## Chain 4: ## Chain 4: Gradient evaluation took 3e-06 seconds ## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds. ## Chain 4: Adjust your expectations accordingly! ## Chain 4: ## Chain 4: ## Chain 4: Iteration: 1 / 5000 \[ 0%\] (Warmup) ## Chain 4: Iteration: 500 / 5000 \[ 10%\] (Warmup) ## Chain 4: Iteration: 1000 / 5000 \[ 20%\] (Warmup) ## Chain 4: Iteration: 1500 / 5000 \[ 30%\] (Warmup) ## Chain 4: Iteration: 2000 / 5000 \[ 40%\] (Warmup) ## Chain 4: Iteration: 2500 / 5000 \[ 50%\] (Warmup) ## Chain 4: Iteration: 2501 / 5000 \[ 50%\] (Sampling) ## Chain 4: Iteration: 3000 / 5000 \[ 60%\] (Sampling) ## Chain 4: Iteration: 3500 / 5000 \[ 70%\] (Sampling) ## Chain 4: Iteration: 4000 / 5000 \[ 80%\] (Sampling) ## Chain 4: Iteration: 4500 / 5000 \[ 90%\] (Sampling) ## Chain 4: Iteration: 5000 / 5000 \[100%\] (Sampling) ## Chain 4: ## Chain 4: Elapsed Time: 0.012823 seconds (Warm-up) ## Chain 4: 0.014169 seconds (Sampling) ## Chain 4: 0.026992 seconds (Total) ## Chain 4: ## Inference for Stan model: 6dcfbccbf2f063595ccc9b93f383e221. ## 4 chains, each with iter=5000; warmup=2500; thin=1; ## post-warmup draws per chain=2500, total post-warmup draws=10000.## ## mean se\_mean sd 10% 90% n\_eff Rhat ## theta 0.27 0.00 0.09 0.16 0.39 3821 1## lp__ -13.40 0.01 0.73 -14.25 -12.90 3998 1## # 提取后验抽样# 计算后均值(估计)mean(theta_draws) ## \[1\] 0.2715866 # 计算后验区间 ## 10% 90% ## 0.1569165 0.3934832 ggplot(theta\_draws\_df, aes(x=theta)) + geom_histogram(bins=20, color="gray")
RStan:MAP,MLE
Stan的估算优化;两种观点:
- _最大后验_估计_(MAP)_。
- _最大_似然估计(_MLE_)。
optimizing(model, data=c("N", "y")) ## $par ## theta ## 0.4 ## ## $value ## \[1\] -3.4## ## $return_code ## \[1\] 0
种群竞争模型 ---Lotka-Volterra模型
- 洛特卡(Lotka,1925)和沃尔泰拉(Volterra,1926)制定了参数化微分方程,描述了食肉动物和猎物的竞争种群。
- 完整的贝叶斯推断可用于估计未来(或过去)的种群数量。
- Stan用于对统计模型进行编码并执行完整的贝叶斯推理,以解决从噪声数据中推断参数的逆问题。
在此示例中,我们希望根据公司每年收集的毛皮数量,将模型拟合到1900年至1920年之间各自种群的加拿大猫科食肉动物和野兔猎物。
数学模型
我们表示U(t)和V(t)作为猎物和捕食者种群数量 分别。与它们相关的微分方程为:
这里:
- α:猎物增长速度。
- β:捕食引起的猎物减少速度。
- γ:自然的捕食者减少速度。
- δ:捕食者从捕食中增长速度。
stan中的Lotka-Volterra
real\[\] dz_dt(data real t, // 时间 real\[\] z, // 系统状态 real\[\] theta, // 参数 data real\[\] x_r, // 数值数据 data int\[\] x_i) // 整数数据{ real u = z\[1\]; // 提取状态 real v = z\[2\];
观察到已知变量:
:表示在时间 的 物种数量
必须推断未知变量):
初始状态: :k的初始物种数量。
后续状态 :在时间t的物种数量k。
参量 。
假设误差是成比例的(而不是相加的):
等效:
与
建立模型
已知常数和观测数据的变量。
data { int<lower = 0> N; // 数量测量 real ts\[N\]; // 测量次数>0 real y0\[2\]; // 初始数量 real<lower=0> y\[N,2\]; // 后续数量} 未知参数的变量。 parameters { real<lower=0> theta\[4\]; // alpha, beta, gamma, delta real<lower=0> z0\[2\]; // 原始种群 real<lower=0> sigma\[2\]; // 预测误差} 先验分布和概率。 model { // 先验 sigma ~ lognormal(0, 0.5); theta\[{1, 3}\] ~ normal(1, 0.5); // 似然(对数正态) for (k in 1:2) { y0\[k\] ~ lognormal(log(z0\[k\]), sigma\[k\]);
我们必须为预测的总体定义变量 :
- 初始种群(
z0)。 - 初始时间(
0.0),时间(ts)。 - 参数(
theta)。 - 最大迭代次数(
1e3)。
Lotka-Volterra参数估计 print(fit, c("theta", "sigma"), probs=c(0.1, 0.5, 0.9)) 获得结果: mean se\_mean sd 10% 50% 90% n\_eff Rhat ## theta\[1\] 0.55 0 0.07 0.46 0.54 0.64 1168 1## theta\[2\] 0.03 0 0.00 0.02 0.03 0.03 1305 1## theta\[3\] 0.80 0 0.10 0.68 0.80 0.94 1117 1## theta\[4\] 0.02 0 0.00 0.02 0.02 0.03 1230 1## sigma\[1\] 0.29 0 0.05 0.23 0.28 0.36 2673 1## sigma\[2\] 0.29 0 0.06 0.23 0.29 0.37 2821 1
分析所得结果:
- Rhat接近1表示收敛;n_eff是有效样本大小。
- 10%,后验分位数;例如
- 后验均值是贝叶斯点估计:α=0.55。
- 后验平均估计的标准误为0。
- α的后验标准偏差为0.07。