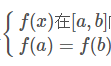高等数学的学习躲不过中值定理,而这部分内容又是有些难度,由于检索相关三大微分中值定理定理的证明并没有满意的文章,便自己整理了一篇供自己参考,希望也能为各位读者提供一些帮助!
1 罗尔定理
描述
如果 R 上的函数 f(x) 满足以下条件:(1)在闭区间 [a,b] 上连续,(2)在开区间 (a,b) 内可导,(3)f(a)=f(b),则至少存在一个 ξ∈(a,b),使得 f’(ξ)=0。
证明
因为函数 f(x) 在闭区间[a,b] 上连续,所以存在最大值与最小值,分别用M 和 m 表示,分两种情况讨论:
- 若 M=m,则函数 f(x) 在闭区间 [a,b] 上必为常函数,结论显然成立。
- 若 M>m,则因为 f(a)=f(b) 使得最大值 M 与最小值 m 至少有一个在 (a,b) 内某点ξ处取得,从而ξ是f(x)的极值点,
又条件 f(x) 在开区间 (a,b) 内可导得,f(x) 在 ξ 处取得极值,由费马引理推知:f’(ξ)=0。
助解
- 费马引理,总结就一句话:可导函数极值点为零
- 若M>m的情况借助图像,便于理解
2 拉格朗日中值定理
描述
证明
注:证法不唯一
通过一段时间的中值定理相关证明题的学习,不难发现辅助函数的构造在解题中的重要性。
3 柯西中值定理
参考链接
1. 知乎拉格朗日定理证明
2. 百度知道