归并排序 7月15日 【今日算法】

今天分享的的内容涉及以下两个问题：

1. 归并排序的迭代实现方式；
2. 实现一个原地归并排序（In-Place Merge Sort）；

归并排序的迭代实现

在正式看代码前，希望你心中清楚归并排序的递归实现方式，不熟悉也无妨，看这篇文章 [图解「归并排序」算法（修订版）]文章。

迭代和递归（Iteration & Recursion）本就心心相惜，你中有我，我中有你，任何一个算法的递归实现都可以将其变成一个迭代的实现方式，只要代价足够小，收益（获得的空间和时间效率的提升）足够高就可以。

归并排序同样可以做到，只是归并排序的迭代实现方式较为特殊，不像大多数递归与迭代的转化，归并排序并不需要程序中出现一个显式的 stack 辅助栈，但同样能够去掉递归调用，以迭代的方式实现归并排序。

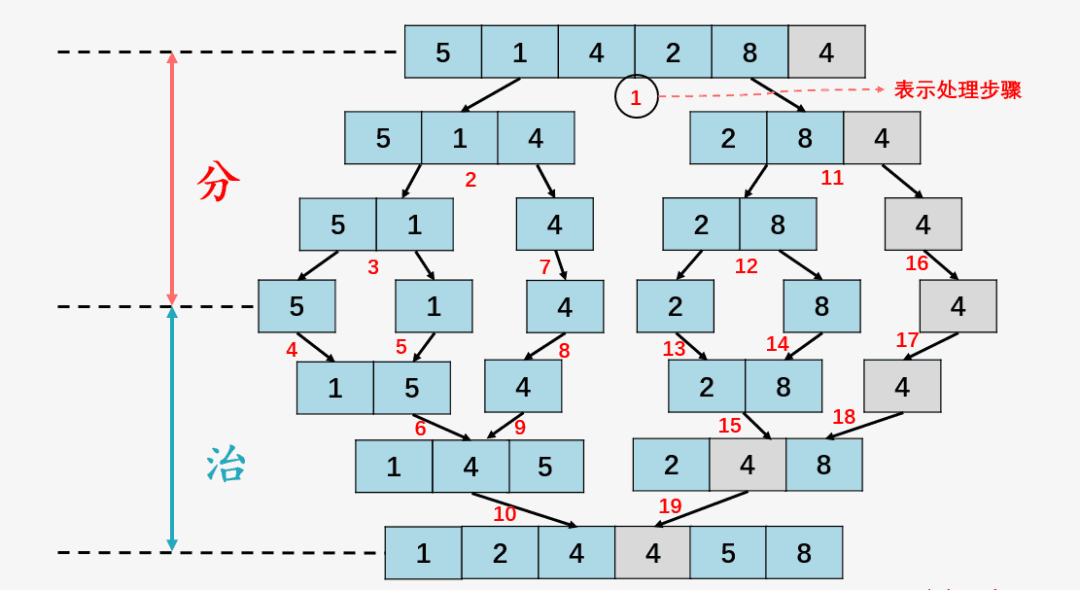
这张图一定很熟悉了，这就是标准的递归实现过程中的分与治，而采用迭代实现时，策略上有两点发生了变化：

1. 分的方式采用循环（迭代），而不是递归的方式；
2. 分的策略和递归的方式有别，依旧符合归并排序的思想；

我们依旧以下面的数组为例说明（感觉这个数组万能，哈哈）：

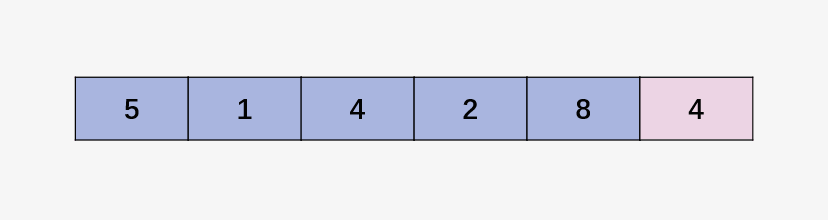
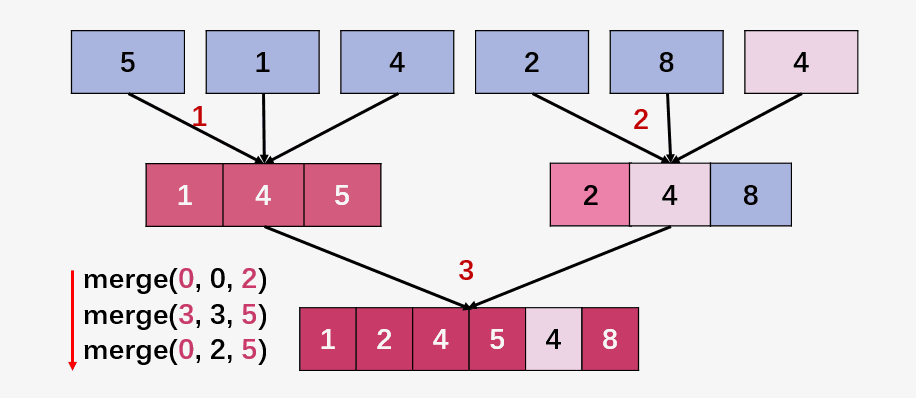
第一步：合并 5 和 1

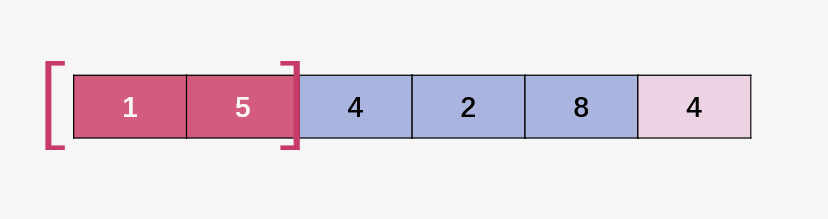
第二步：合并 4 和 2

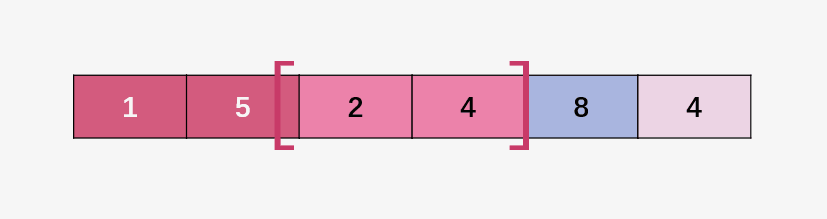
第三步：合并 8 和 4 ；

第四步：合并 [1,5,2,4]

第五步：合并 [4,8]

第六步：合并 [1,2,4,5,4,8]

看到这里，并不能清晰地看出归并排序迭代和递归之间的差异，客官莫急：

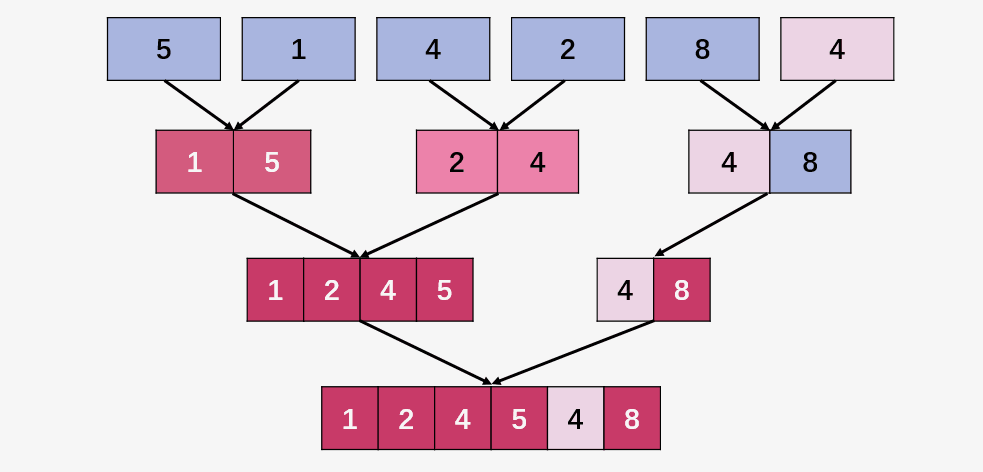
这次就会清晰可见了，归并排序的迭代实现方式中的合并顺序与递归明显不同，递归是将长度为 n 的原始数组一分为二，然后再将两个（1/2）的数组再一分为二，直到分为n个长度为1的元素。然后两两按大小合并，如此反复，直到最后形成包含 n 个数的一个有序数组。

而迭代就不同了，默认将数组当中的元素当做 n 个长度为1的元素；依次按照 2 个一组合并，4 个元素为一组进行合并（不足 4 个，比如 [4,8] ，不足 4 个就按照剩余个数 2 合并），....，最后以 n/2 个元素为一组进行合并，得到我们的有序数组。

迭代实现中，仅从图中似乎看不到分的过程，但事实上，合并前已经进行了分，只不过这个分与递归调用的分不同，而是采用迭代。

忽略合并的实现细节，我们仅看一下迭代的实现方式。

static void mergeSort(int arr[], int n) 
{ 
 
    int curr_size; //标识当前合并的子数组的大小，从 1 已知到 n/2
    int left_start; //标识当前要合并的子数组的起点
    for (curr_size = 1; curr_size <= n-1; curr_size = 2*curr_size) 
    { 
        for (left_start = 0; left_start < n-1; left_start += 2*curr_size) 
        { 
            int mid = Math.min(left_start + curr_size - 1, n-1); 
 
            int right_end = Math.min(left_start + 2*curr_size - 1, n-1);
   
            merge(arr, left_start, mid, right_end);
         } 
     } 
} 
//合并略

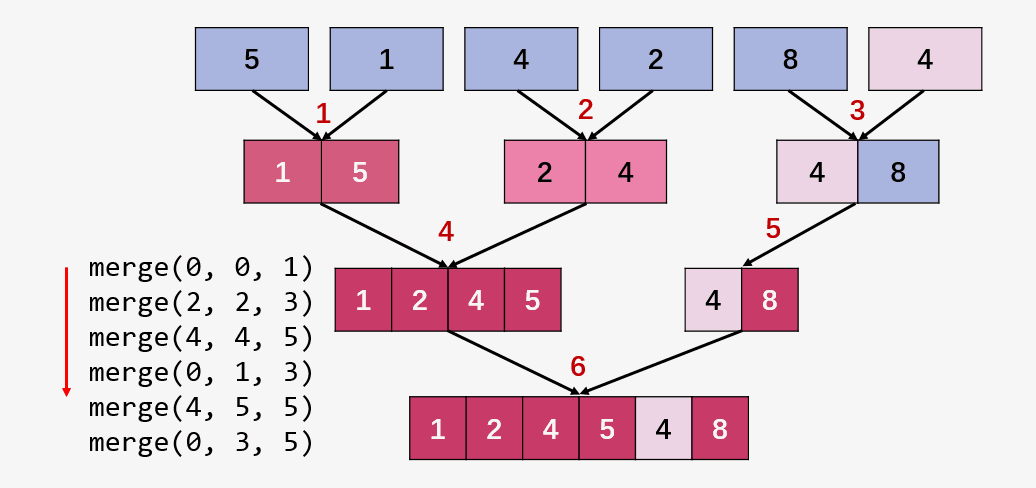
归并排序的迭代实现就是将递归中 递 的操作修改成了两层的 for 循环，为了理解这两层循环所进行的操作，建议最好自己将数组 [5,1,4,2,8,4] 代进去手动的计算一遍，下图中给出了merge(arr, left_start, mid, right_end); 函数依次调用数据：

请问如何用迭代实现三路归并排序？

答案很简单了，将上面提供的二路归并排序的迭代实现中的所有 2 替换为 3，合并过程将变成下图：

改日再详述 3 路归并排序，接着看第二个问题。

原地归并排序

所谓原地排序（In-place Sort）就是空间复杂度为O(1) 的排序算法。[图解「归并排序」算法（修订版）]中所讲的归并排序空间复杂度为O(n) ，时间复杂度为O(nlogn) ，其中O(n) 的空间复杂度是由 merge(arr, left, mid, right) 函数所造成的，所以关于这个问题的解决就是折腾 merge 函数。

该如何折腾呢？看栗子（哈哈，就是废话少）。

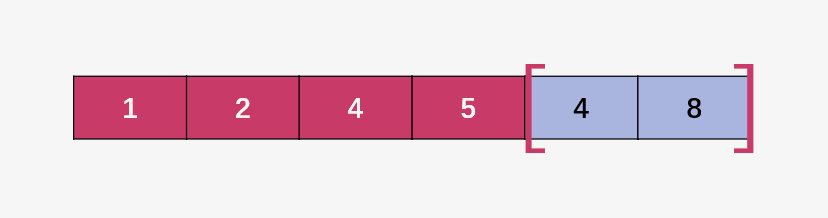
同样以最后一次合并为例：

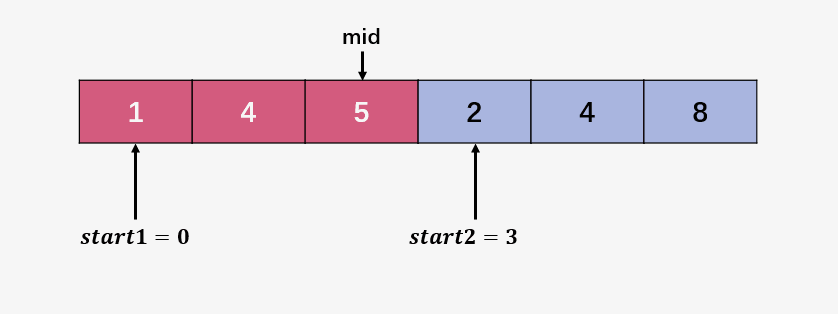
这里的 start1 、start2 还有 mid 的初始设置就不多说了，看原地合并过程即可。

第一步：比较 start1 指向的元素 1 和 start2 指向的元素 2 ，1 < 2 ，所以直接将 start1右移，即 start1++ .

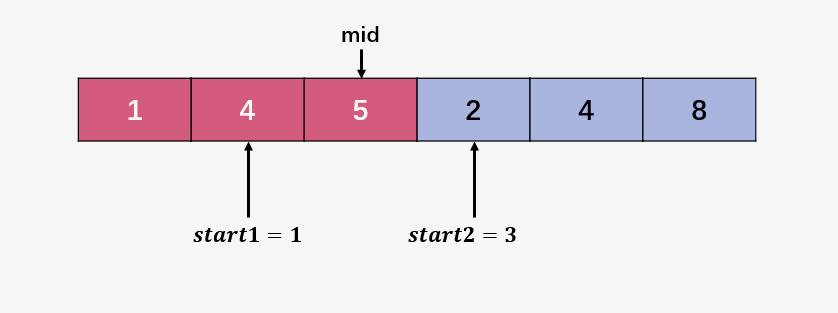
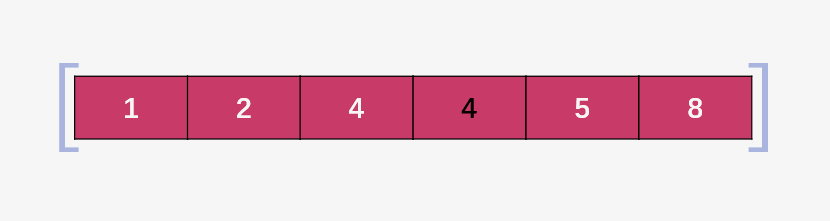
第二步：比较 start1 指向的元素 4 和 start2 指向的元素 2 ，4 > 2 ，此时不使用额外空间实现合并操作，将 start2 之前，start1 (包含 start1) 之后的元素向后移动，并将 2 拷贝到 start1 所指向的位置，然后将 start1 、start2 还有 mid 均向后移动：

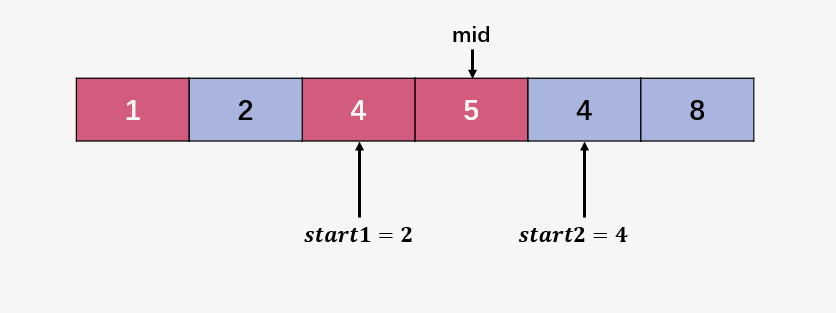
第三步：比较 start1 指向的元素 4 和 start2 指向的元素 4 ，4 = 4 ，所以直接将 start1右移，即 start1++ .

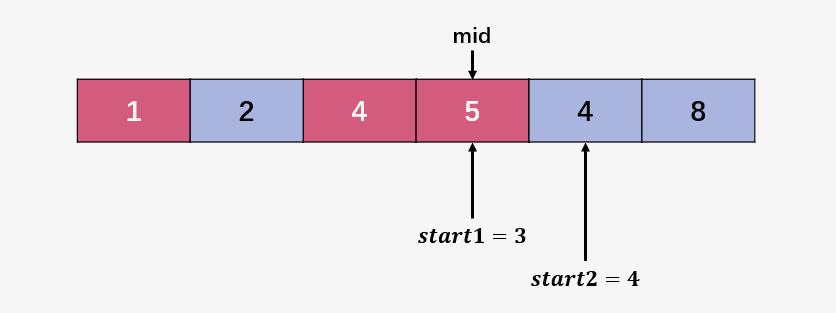
第四步：与第二步类似，比较 start1 指向的元素 5 和 start2 指向的元素 4 ，5 > 4 ，将 4向前移动，将 5 向后移动，然后将 start1 、start2 还有 mid 均向后移动：

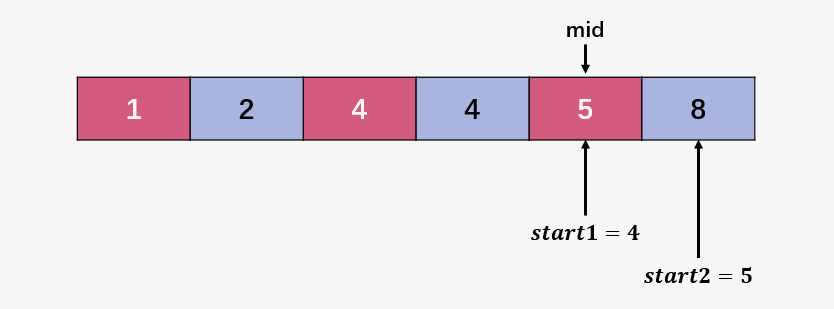
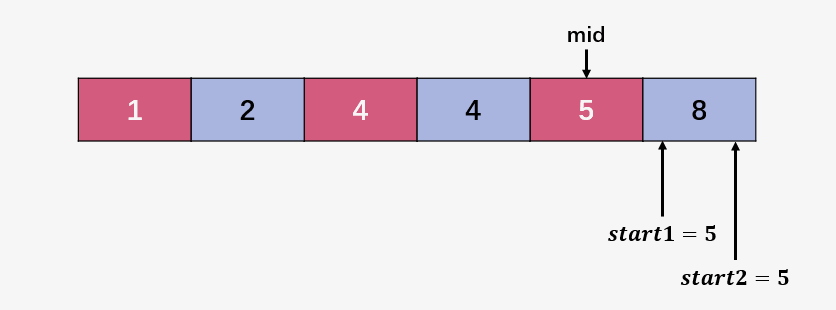
第五步：比较 start1 指向的元素 5 和 start2 指向的元素 8 ，**5 < 8 ** ，直接将 start1右移，即 start1++ ；此时 start1 > mid ,表明合并完成了。

空间复杂度为O(1) 的合并操作的实现代码：

static void merge(int arr[], int start1, int mid, int end){
    int start2 = mid + 1;
    
    //如果 mid 小于等于 mid+1 的元素，表明数组已经有序，不需要合并
    if(arr[mid] <= arr[start2]){
        return;
    }
    
    while(start1 <= mid && start2 <= end){
        if(arr[start1] <= arr[start2]){
            start1++;
        }
        else{
            int value = arr[start2];
            int index = start2;
            
            //将 [start1,start2 - 1]中的元素向后移动
            while(index != start1){
                arr[index] = arr[index - 1];
                index--;
            }
            
            arr[start1] = value;
            
            start1++;
            mid++;
            start2++;
        }
    }
}

注意这个合并操作中涉及到了两个嵌套的 while 循环，所以与空间复杂度为O(n) ，时间复杂度为O(nlogn) 的标准实现相比，这种合并策略虽然将空间复杂度降到了O(1) ，但同时也牺牲了时间复杂度，时间复杂度变成了O(n²) .

时间复杂度和空间复杂度就似阴阳之术，得失之理，生死之界；要得其一，必失其一，这个世上没有两全其美的事情！

[「归并排序：题目一」如何实现一个空间复杂度为 O(1) 的归并排序？]这篇文章中分享的就是一种空间复杂度为O(1) ，而且时间复杂度认为O(nlogn) 的方法呀！

那是因为我们使用了数学技巧，但是同时也伴随着频繁地求余和除法运算，直白点就是增加了资源消耗。

来源 | 景禹

作者 | 景禹