
Floyd 算法又称插点法,它的核心思想是动态规划,常用来求解图中任意一对顶点之间的最短路径问题。
D[n][n],其中D[i][j]表示,顶点i到顶点j的距离。D[n][n]。D[i][k] + D[k][j] < D[i][j],那说明顶点i经过顶点k再到达j,比直接到达j要近。所以更新D[i][j]:D[i][j] = D[i][k] + D[k][j]。D[i][j] = min(D[i,k]+D[k,j],D[i,j]);Floyd 核心代码:
// Floyd算法
for (int k = 0; k < n; k++) {
// n个顶点依次作为插入点
// 注意插点k是放在第一层循环,后面会解释原因
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
// 遍历各个顶点之间的距离,并用插入点进行更新
D[i][j] = min(D[i][k]+D[k][j], D[i][j]);
}
}
}
有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges 和一个整数distanceThreshold。其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和toi 两个城市之间的双向加权边,distanceThreshold 代表距离阈值。
返回能够到达其他城市数目最少、且路径距离不超过 distanceThreshold 的城市。如果有多个这样的城市,则返回编号最大的城市。
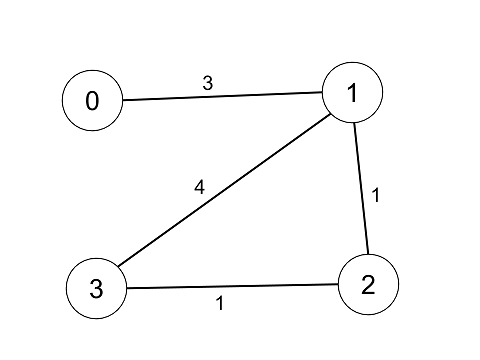
输入:n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]]
distanceThreshold = 4
输出:3
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是:
城市 0 -> [城市 1, 城市 2]
城市 1 -> [城市 0, 城市 2, 城市 3]
城市 2 -> [城市 0, 城市 1, 城市 3]
城市 3 -> [城市 1, 城市 2]
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市,但是我们必须
返回城市 3,因为它的编号最大。
D[n][n]中。D[n][n],统计各个城市在距离不超过 distanceThreshold 的情况下,能到达的其它城市的数量。ret。class Solution {
public:
int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
// 定义二维D向量,并初始化各个城市间距离为INT_MAX(无穷)
vector<vector<int>> D(n, vector<int>(n, INT_MAX));
// 根据edges[][]初始化D[][]
for (auto& e : edges) {
// 无向图两个城市间的两个方向距离相同
D[e[0]][e[1]] = e[2];
D[e[1]][e[0]] = e[2];
}
// Floyd算法
for (int k = 0; k < n; k++) {
// n个顶点依次作为插入点
for (int i = 0; i < n; i++) {
for (int j = i+1; j < n; j++) {
if (D[i][k] == INT_MAX || D[k][j] == INT_MAX) {
// 这些情况都不符合下一行的if条件,
// 单独拿出来只是为了防止两个INT_MAX相加导致溢出
continue;
}
D[i][j] = min(D[i][k]+D[k][j], D[i][j]);
D[j][i] = D[i][j];
}
}
}
// 选择出能到达其它城市最少的城市ret
int ret;
int minNum = INT_MAX;
for (int i = 0; i < n; i++) {
int cnt = 0;
for (int j = 0; j < n; j++) {
if (i != j && D[i][j] <= distanceThreshold) {
cnt++;
}
}
if (cnt <= minNum) {
minNum = cnt;
ret = i;
}
}
return ret;
}
};
这个源自 Floyd 的核心思想--动态规划,代码中的二维状态转移方程D[i][j] = min(D[i,k]+D[k,j],D[i,j]);,其实是从三维简化得到的。
我们不妨从最初的三维说起,思路和二维一样:
D[n][n][n],其中D[k][i][j]表示顶点i, 顶点j通过前k个顶点(0~k)得到的最短距离。D[k][i][j]是从D[k-1][i][j]和D[k-1][i][k] + D[k-1][k][j]两者中值较小的一个转移得到的,也就是说要在前k-1个顶点已经插入,更新距离矩阵状态之后,第k个顶点才能作为插入顶点。D[k][i][j] = min(D[k-1][i][j], D[k-1][i][k] + D[k-1][k][j])。k的作用是标志到达了第几个插入点,也就是状态数组到达了哪个状态,不用刻意记录,于是减去第一维就变成了二维。明白了 Floyd 的三维 dp 思想,根据状态转移方程在编码时就很自然的会将 k 放在第一层循环,而将k放在最后一层则是错误的编码。
因为两个城市之间是互通的,也就是无向图,那计算出了D[i][j]就没必要重复计算D[j][i]了,于是我们可以把 Floyd 算法的最后一层循环的j 改成从i+1 开始计数,同时在计算出D[i][j]后直接赋值给D[j][i]。
// Floyd算法
for (int k = 0; k < n; k++) {
// n个顶点依次作为插入点
for (int i = 0; i < n; i++) {
for (int j = i+1; j < n; j++) {
if (D[i][k] == INT_MAX || D[k][j] == INT_MAX) {
// 这些情况都不符合下一行的if条件,
// 单独拿出来只是为了防止两个INT_MAX相加导致溢出
continue;
}
D[i][j] = min(D[i][k]+D[k][j], D[i][j]);
D[j][i] = D[i][j];
}
}
}
感谢您的观看!希望您能有所收获。
来源 | 小小算法
作者 | 小小算法
版权声明:本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单进行举报,一经查实,本社区将立刻删除涉嫌侵权内容。