支持向量机内容练习

首先要做的就是研究简单的二维数据集，看看线性的SVM是如何在不同C值(类似于线性/逻辑回归中的正则化项)的数据集上工作的。

加载数据

import numpy as np  
import pandas as pd  
import matplotlib.pyplot as plt  
import seaborn as sb  
from scipy.io import loadmat  
%matplotlib inline

raw_data = loadmat('data/ex6data1.mat')  
raw_data

{'X': array([[ 1.9643  ,  4.5957  ],
        [ 2.2753  ,  3.8589  ],
        [ 2.9781  ,  4.5651  ],
        ...,
        [ 0.9044  ,  3.0198  ],
        [ 0.76615 ,  2.5899  ],
        [ 0.086405,  4.1045  ]]),
 '__globals__': [],
 '__header__': 'MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Sun Nov 13 14:28:43 2011',
 '__version__': '1.0',
 'y': array([[1],
        [1],
        [1],
        ...,
        [0],
        [0],
        [1]], dtype=uint8)}

我们将它可视化为散点图，类标签由符号表示(‘ + ‘为 positive，’ o ‘为negative)。

data = pd.DataFrame(raw_data['X'], columns=['X1', 'X2'])  
data['y'] = raw_data['y']

positive = data[data['y'].isin([1])]  
negative = data[data['y'].isin([0])]

fig, ax = plt.subplots(figsize=(12,8))  
ax.scatter(positive['X1'], positive['X2'], s=50, marker='x', label='Positive')  
ax.scatter(negative['X1'], negative['X2'], s=50, marker='o', label='Negative')  
ax.legend()

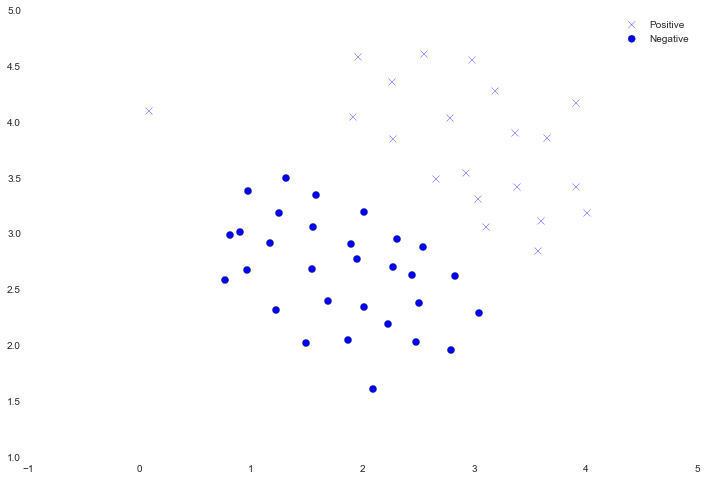
注意，有一个比其他值更positive的离群值的例子。这些类仍然是线性可分的，但它是一个非常紧密的组合。我们将训练一个线性支持向量机来学习类边界。在这个练习中，我们不需要从头开始执行SVM，所以我将使用scikit- learn的内置工具。

from sklearn import svm  
svc = svm.LinearSVC(C=1, loss='hinge', max_iter=1000)  
svc

LinearSVC(C=1, class_weight=None, dual=True, fit_intercept=True,
     intercept_scaling=1, loss='hinge', max_iter=1000, multi_class='ovr',
     penalty='l2', random_state=None, tol=0.0001, verbose=0)

第一次试验取值C=1，观察它怎样运行

svc.fit(data[['X1', 'X2']], data['y'])  
svc.score(data[['X1', 'X2']], data['y'])

0.98039215686274506

看来它错误的分类了离散值。让我们看看当C值更大时会怎样。

svc2= svm.LinearSVC(C=100, loss='hinge', max_iter=1000) 
svc2.fit(data[['X1','X2']], data['y']) 
svc2.score(data[['X1','X2']], data['y'])

1.0

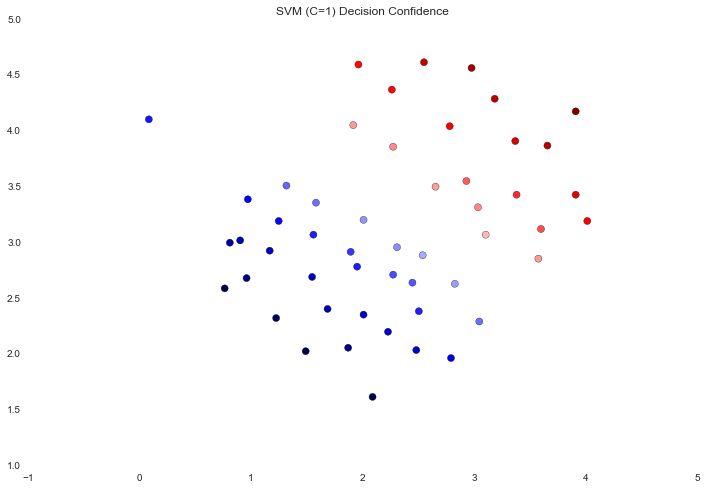
这次我们得到了更好的训练集的分类。然而随着C值的增加，我们创建了一个不再适合该数据的决策边界。我们可以通过每个等级预测的置信度来可视化它，这是点与超平面的距离的函数。

data['SVM 1 Confidence'] = svc.decision_function(data[['X1', 'X2']])

fig, ax = plt.subplots(figsize=(12,8))  
ax.scatter(data['X1'], data['X2'], s=50, c=data['SVM 1 Confidence'], cmap='seismic')  
ax.set_title('SVM (C=1) Decision Confidence')

data['SVM 1 Confidence'] = svc.decision_function(data[['X1', 'X2']])

fig, ax = plt.subplots(figsize=(12,8))  
ax.scatter(data['X1'], data['X2'], s=50, c=data['SVM 1 Confidence'], cmap='seismic')  
ax.set_title('SVM (C=1) Decision Confidence')

data['SVM 2 Confidence'] = svc2.decision_function(data[['X1', 'X2']])

fig, ax = plt.subplots(figsize=(12,8))  
ax.scatter(data['X1'], data['X2'], s=50, c=data['SVM 2 Confidence'], cmap='seismic')  
ax.set_title('SVM (C=100) Decision Confidence')

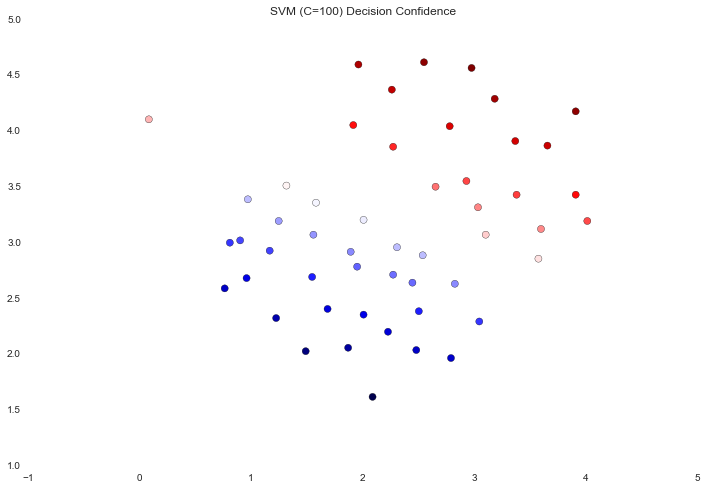
边界附近点的颜色差别有点微妙。在第一个图像中，边界附近的点是强烈的红色或蓝色，表明它们在超平面的可靠范围内。在第二个图像中不是的，这样其中一些点几乎是白色的，表明它们与超平面直接相邻。

现在我们将从线性SVM转移到能够使用内核进行非线性分类的SVM。首先，我们需要实现一个高斯核函数。为了完全透明，尽管scikit- learn有一个高斯内核，我们仍然从头开始实现高斯核函数 。

def gaussian_kernel(x1, x2, sigma):  
    return np.exp(-(np.sum((x1 - x2) ** 2) / (2 * (sigma ** 2))))

x1 = np.array([1.0, 2.0, 1.0])  
x2 = np.array([0.0, 4.0, -1.0])  
sigma = 2  
gaussian_kernel(x1, x2, sigma)

0.32465246735834974

这个结果与预期值相匹配。接下来，我们将检查另一个非线性决策边界的数据集。

raw_data = loadmat('data/ex6data2.mat')

data = pd.DataFrame(raw_data['X'], columns=['X1', 'X2'])  
data['y'] = raw_data['y']

positive = data[data['y'].isin([1])]  
negative = data[data['y'].isin([0])]

fig, ax = plt.subplots(figsize=(12,8))  
ax.scatter(positive['X1'], positive['X2'], s=30, marker='x', label='Positive')  
ax.scatter(negative['X1'], negative['X2'], s=30, marker='o', label='Negative')  
ax.legend()

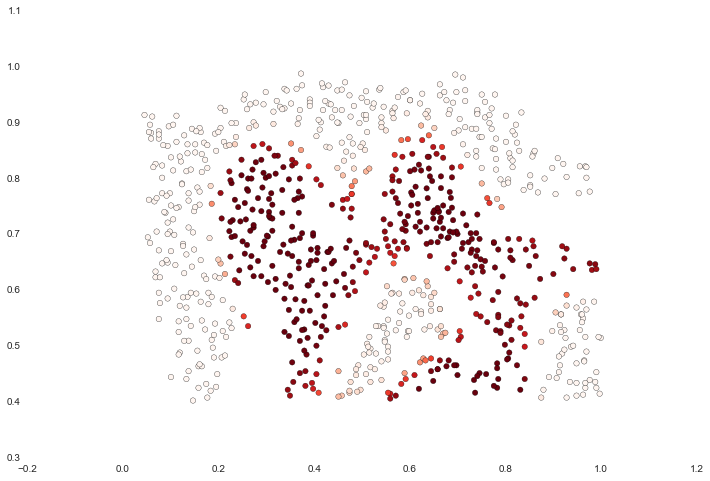
对于这个数据集，我们将使用内置的RBF内核构建一个支持向量机分类器，并检查它在训练数据上的准确性。为了使决策边界可视化，这次我们将基于具有负类标签的实例预测概率来遮蔽点。我们从结果中看到大部分都是正确的。

svc = svm.SVC(C=100, gamma=10, probability=True)  
svc.fit(data[['X1', 'X2']], data['y'])  
data['Probability'] = svc.predict_proba(data[['X1', 'X2']])[:,0]

fig, ax = plt.subplots(figsize=(12,8))  
ax.scatter(data['X1'], data['X2'], s=30, c=data['Probability'], cmap='Reds')

对于第三个数据集，我们得到了训练和验证集，并基于验证集性能为SVM模型寻找最优超参数。尽管我们可以很容易地使用scikit- learn的内置网格搜索来实现这一点，但为了更多的练习，我们将从头开始实现一个简单的网格搜索。

raw_data = loadmat('data/ex6data3.mat')

X = raw_data['X']  
Xval = raw_data['Xval']  
y = raw_data['y'].ravel()  
yval = raw_data['yval'].ravel()

C_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]  
gamma_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]

best_score = 0  
best_params = {'C': None, 'gamma': None}

for C in C_values:  
    for gamma in gamma_values:
        svc = svm.SVC(C=C, gamma=gamma)
        svc.fit(X, y)
        score = svc.score(Xval, yval)

        if score > best_score:
            best_score = score
            best_params['C'] = C
            best_params['gamma'] = gamma

best_score, best_params

(0.96499999999999997, {'C':0.3,'gamma':100})

现在我们继续练习的最后一部分。在这个部分，我们的目标是使用SVMs构建一个垃圾邮件过滤器。在练习文本中，有一个任务需要对一些文本进行预处理，以使获得适合SVM的数据格式，这个任务非常简单，而其他预处理步骤（例如HTML删除、词干、规范化等）都已经完成了。我不会重复这些步骤，而是跳过机器学习任务，其中包括从预处理的训练中创建分类器，以及由垃圾邮件和非垃圾邮件转换为单词发生向量的测试数据集。

svc = svm.SVC()  
svc.fit(X, y)

print('Test accuracy = {0}%'.format(np.round(svc.score(Xtest, ytest) * 100, 2)))

Test accuracy= 95.3%

这个结果与默认参数有关。我们可能会使用一些参数调优来提高它的精度，但是95%的精度仍然不差。