欧氏距离和曼哈顿距离

欧氏距离（也称为欧几里得度量），是应用勾股定理计算两个点之间的直线距离，也就是指m维空间两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。

下面是欧式距离的公式（分别是二维空间，三维空间，n维空间）：

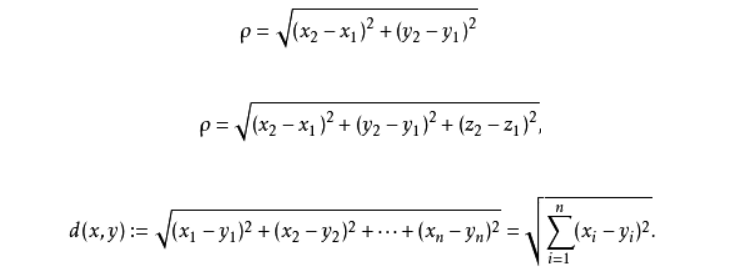
　曼哈顿距离表示的是两个点在标准坐标系上绝对轴距之和，是种使用在几何度量空间的几何学用语。

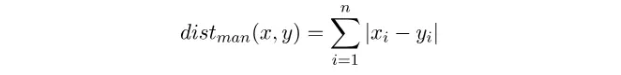
例如在平面上，坐标（x1, y1）的i点与坐标（x2, y2）的j点的曼哈顿距离为：
d(i,j)=|X1-X2|+|Y1-Y2|

如图所示，很直接明了的理解欧氏距离和曼哈顿距离：
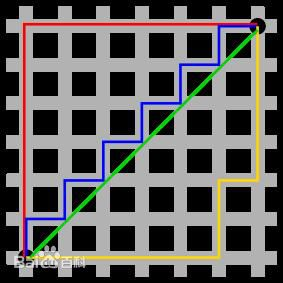
图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。

欧氏距离和曼哈顿距离的Python实现：

import numpy as np
 
def manhattan_distance(vec1, vec2):
    """
    This method implements the manhattan distance metric
    :param p_vec: vector one
    :param q_vec: vector two
    :return: the manhattan distance between vector one and two
    """
    return np.sum(np.fabs(vec1 - vec2))
 
def edclidean_distance(vec1, vec2):
    """
    This method implements the edclidean distance metric
    :param vec1: vector one
    :param vec2: vector two
    :return: the edclidean distance between vector one and two
    """
    # 方法一
    distance = np.sqrt(np.sum(np.square(vec1 - vec2)))
 
    # method 2
    dist = np.linalg.norm(vec1 - vec2)
    return distance