随机变量专题及其python实现(概率分布，二项分布，正态分布，卡方分布，t分布，F分布及变量相关性分析等)(下)

2022-04-19 757

版权

本文内容由阿里云实名注册用户自发贡献，版权归原作者所有，阿里云开发者社区不拥有其著作权，亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容，填写侵权投诉表单进行举报，一经查实，本社区将立刻删除涉嫌侵权内容。

简介： 随机变量专题及其python实现(概率分布，二项分布，正态分布，卡方分布，t分布，F分布及变量相关性分析等)(下)

4. 正态分布

4.1 正态分布概述

正态分布(Normal Distribution)又名高斯分布(Gaussiam Distribution)，是人们最常用的描述连续型随机变量的概率分布。在金融学研究中，收益率等变量的分布假定为正态分布或者对数正态分布(取对数后服从正态分布)。因为形状的原因，正态分布曲线也被经常称为钟形曲线。
在这里插入图片描述

4.2 Python正态分布相关函数

正态分布随机数的生成函数是normal()，其语法为：
normal(loc=0.0, scale=1.0, size=None)

参数loc：表示正态分布的均值
参数scale：表示正态分布的标准差，默认为1
参数size：表示生成随机数的数量

# 生成五个标准正态分布随机数
Norm = np.random.normal(size=5)
# 求生成的正态分布随机数的密度值
stats.norm.pdf(Norm)
# 求生成的正态分布随机数的累积密度值
stats.norm.cdf(Norm)

在这里插入图片描述
绘制正态分布PDF

# 注意这里使用的pdf和cdf函数是norm包里的
u=0  
sigma=1
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.title('X~N({},{})正态分布PDF'.format(u,sigma**2))
x = np.linspace(-5,5,100000)  # 设定分割区间
y1 = stats.norm.pdf(x,u,sigma**2)
plt.plot(x,y1)
plt.tight_layout()  # 自动调整子图，使之充满画布整个区域
plt.show()

图像效果：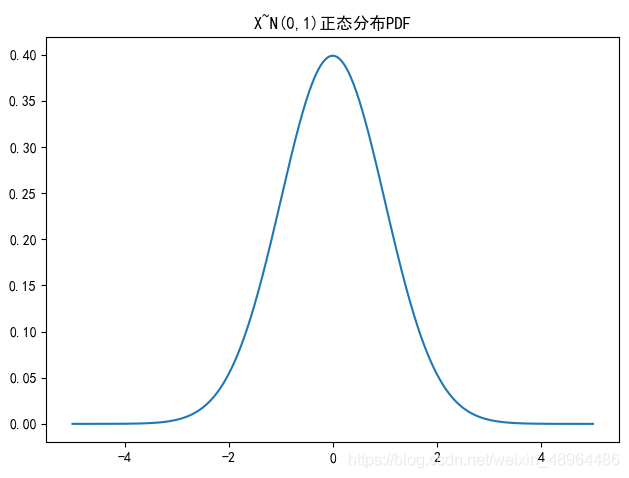
在这里插入图片描述

绘制正态分布CDF

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.title('X~N({},{})正态分布CDF'.format(u,sigma**2))
x = np.linspace(-5,5,100000)  # 设定分割区间
y2 = stats.norm.cdf(x,u,sigma**2)
plt.plot(x,y2)
plt.tight_layout()  
plt.show()

图像效果：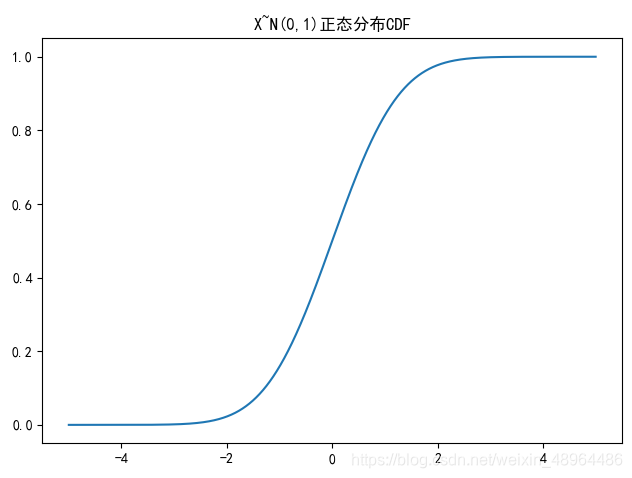
在这里插入图片描述

4.3 正态分布在金融市场的应用

VAR(Value at Risk)，即在险价值。是指在一定概率水平(α%)下，某一金融资产或金融资产组合在未来特定一段时间内的最大可能的损失，该定义可表达为：在这里插入图片描述

这里用到了ppf() 函数，来获取指定分位数的累积密度值。
假设平安银行股价2020年日收益率序列服从正态分布，下面用Python来求解当概率水平为5%时平安银行股价日收益率在2021年初个交易日的VaR:

# 上边已经定义过ret变量了，为平安银行2020年股价日收益率数据，
# 这里直接接着使用
ret_mean = ret.mean()   # 求均值
ret_variance = ret.var()  # 求方差
# 查询累积密度值为0.05的分位数
stats.norm.ppf(0.05, ret_mean, ret_variance**0.5)

在这里插入图片描述
也就是说，在2021年的第一个交易日，有95%概率平安银行股票的损失不会超过3.475523569%。
（虽然当天实际跌了3.83，产生了异常值。）

5. 其他连续分布

5.1 卡方分布

若Z₁, Z₂, … Z_n,为n个服从标准正态分布的随机变量，则变量：
在这里插入图片描述

因为n的取值可以不同，所以卡方分布是一族分布而不是一个单独的分布。根据X的表达式，服从卡方分布的随机变量值不可能取负值，其期望值为n，方差为2n。

plt.plot(np.arange(0, 5, 0.002),\
stats.chi.pdf(np.arange(0, 5, 0.002), 3))
plt.title('卡方分布PDF（自由度为3）')

生成图像如下：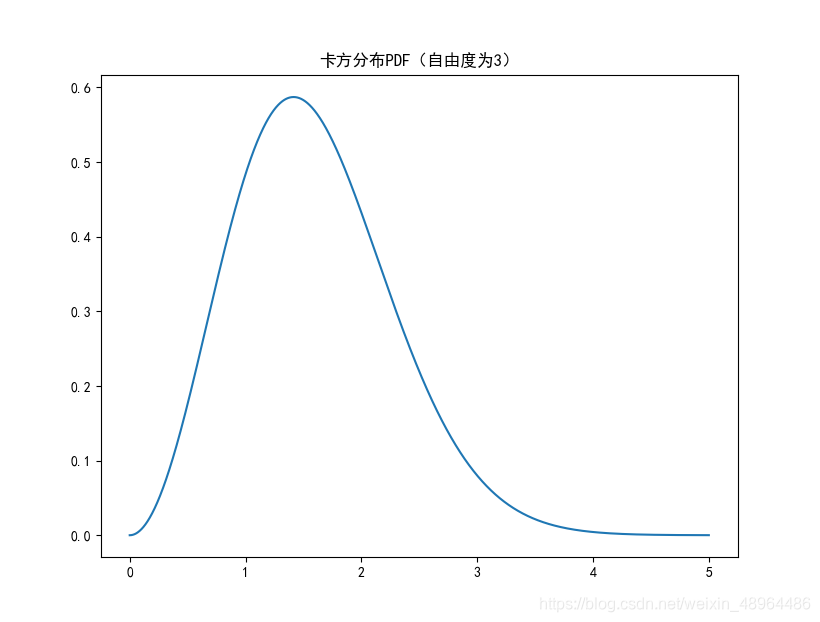
在这里插入图片描述

卡方分布以0为起点，分布是偏斜的，即非对称的，在自由度为3的卡方分布下，大多数值都小于8，查表可知只有5%的值大于7.82%。

5.2 t分布

类似卡方分布，t分布也是整整一族，自由度n不同t分布即不同。
t分布变量取值范围为（−∞,+∞），其期望值与方差存在于否，取值大小均与t分布的自由度有关。

t(1)分布无有限期望值。
t(2)有有限期望值，但方差不存在。
n>2时，t(n)才同时有有限的期望值和方差，其中期望值为0，方差为n/(n-2)，因此自由度越大，变量的方差越小，也就是说分布的离散程度越小。

下边使用Python绘制不同自由度下的t分布的概率分布图：

x = np.arange(-4,4.004,0.004)
plt.plot(x, stats.norm.pdf(x), label='Normal')
plt.plot(x, stats.t.pdf(x,5), label='df=5')
plt.plot(x, stats.t.pdf(x,30), label='df=30')
plt.legend()

结果如图所示：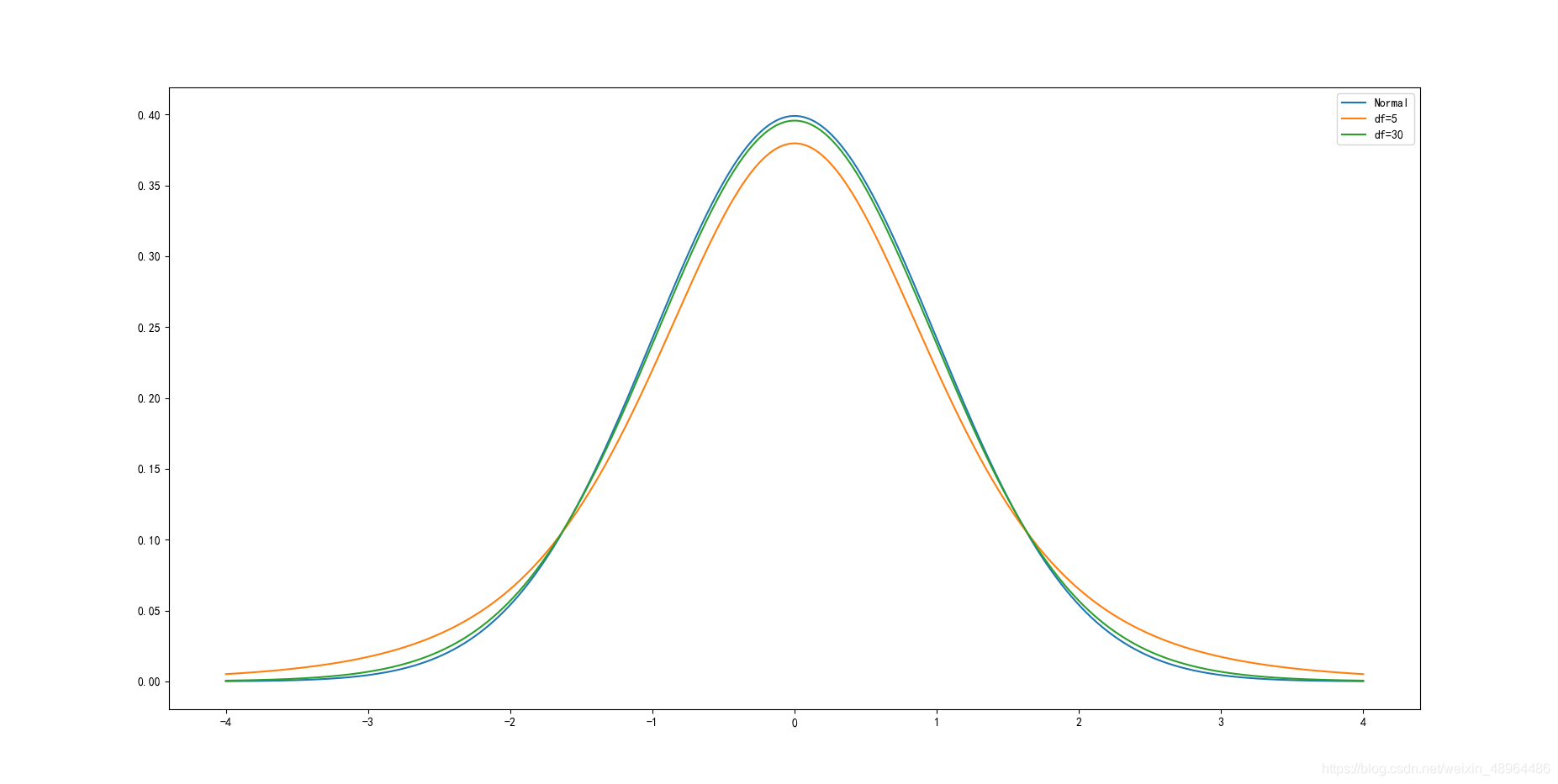
在这里插入图片描述
t分布的pdf曲线是以0为中心，左右对称的单峰分布，其形态变化与自由度n的大小有关，自由度越小，分布越分散；自由度越大，变量在其均值周围的聚集程度越高，也越接近标准正态分布曲线。
自由度为30时，t分布已经接近标准正态分布曲线。相较于标准正态分布，t分布的密度函数呈现出“尖峰厚尾”的特点。在现实中资产收益率分布往往呈现这种形态，因此t分布在对实际抽样结果的刻画上更为精确。t分布是在推断统计中常用的分布。
————

5.3 F分布

plt.plot(np.arange(0,5,0.002),\
stats.f.pdf(np.arange(0,5,0.002), 4, 40))
plt.title('F分布PDF(df1=4, df2=40)')

它的概率密度函数形态如图所示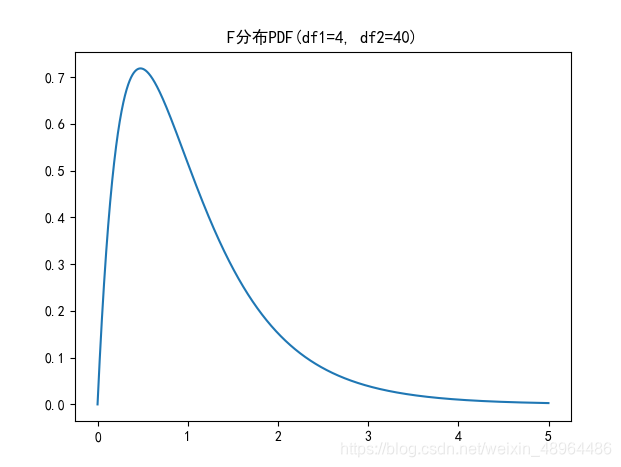
在这里插入图片描述

6. 变量的关系

我们面对的多个随机变量，之间可能会有互相影响。

6.1 联合概率分布

多个变量之间的联合行为可以用联合概率分布(Joint Probability Distribution)来刻画。
若变量X, Y是离散的，其所有可能取值的集合为{a_k}和{b_k}, k=1，2，…，
则X，Y的联合概率质量函数(Joint Probability Mass Function)为：
在这里插入图片描述

6.2变量的独立性

如果随机变量X和Y的联合累积分布函数满足：

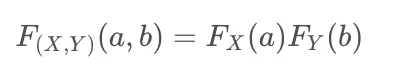
则称X和Y是独立的，否则二者是相依的。

两变量的独立关系也可以表达成，

对于离散型随机变量，此式等价于

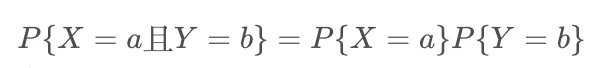
变量之间的相互独立是众多统计分析的基本假设，也是变量之间的基本关系。

6.3 变量的相关性

随机变量X和Y的协方差(Covariance)可以衡量二者之间的关系，描述的是两随机变量与各自期望的偏差共同的变动状况，表达式为：
在这里插入图片描述
协方差为正说明，平均而言变量X、Y与各自期望的偏差呈同方向变动；如果为负，则为反方向变动。
协方差有如下性质：

第二个性质说明，协方差受比例影响，并不能准确地衡量两变量相关性的大小。，不能直接衡量两变量相关性强弱。对协方差进一步处理，清除比例的影响，于是就有了相关系数(Correlation Coefficient):

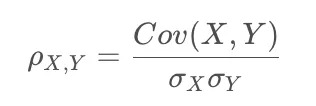
相关系数取值范围为[-1,+1]
ρ=0时，说明两个变量是不相关的。
0<ρ<1时，说明两变量呈正向的线性关系
-1<ρ<0时，说明两变量呈负向的线性关系。

aX和bX的相关性：

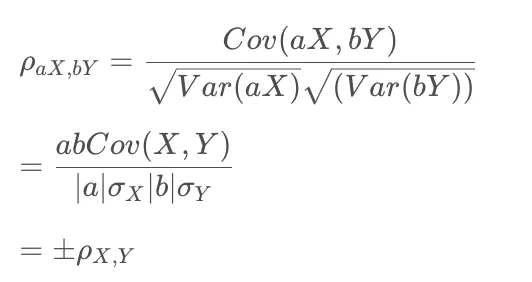
如果变量Y是X的线性变换，满足Y=a+bX，则二者之间的相关系数为：‘
在这里插入图片描述

6.4 上证指数与深证成指相关性分析

上证指数和深证成指是股票市场常用的反映股票市场情况的指数，我们认为两个指数的日收益率可以存在相关的关系。代码如下：

import numpy as np
import tushare as ts
import pandas as pd
token = 'Your Token'   # 输入你的接口密匙，获取方式及相关权限见Tushare官网。
pro = ts.pro_api(token)
# 深证成指
SZindex = pro.index_daily(ts_code='399001.SZ')
SZindex['trade_date'] = pd.to_datetime(SZindex['trade_date'])
SZindex.set_index(['trade_date'], inplace=True)
SZindex = SZindex.sort_index()
# 上证指数
SHindex = pro.index_daily(ts_code='000001.SH')
SHindex['trade_date'] = pd.to_datetime(SHindex['trade_date'])
SHindex.set_index(['trade_date'], inplace=True)
SHindex = SHindex.sort_index()

# 用2020年日收益率数据绘制散点图
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.scatter(SHindex.pct_chg['2020'],SZindex.pct_chg['2020'])
plt.title('上证指数与深证成指2020年收益率散点图')
plt.xlabel('上证指数收益率')
plt.ylabel('深证成指收益率')
plt.show()

生成图像展示如下：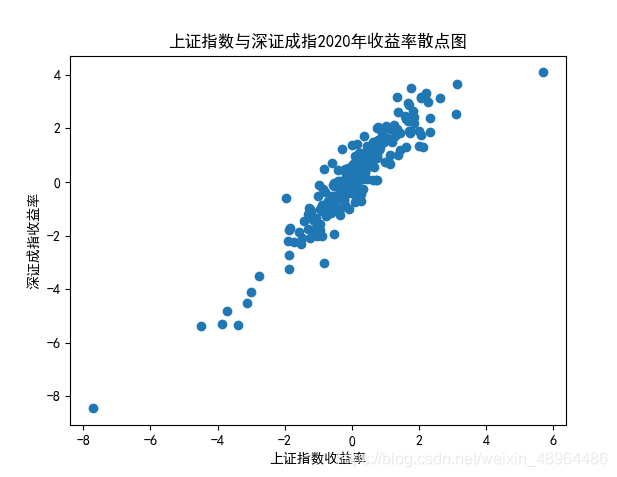
在这里插入图片描述

# 计算上证综指和深证成指收益率相关系数
SHindex.pct_chg['2020'].corr(SZindex.pct_chg['2020'])

在这里插入图片描述
相关系数为0.9308847411746248，可以认为二者存在较强的相关性，二者呈现正向的线性关系。

在这里插入图片描述