- 树到底是个啥
通俗来讲,就是所有顶点都由一些边从而连在了一起,但是不包含回路的图


- 最小生成树又是什么
我们知道上述树的生成是由很多点和边组成的,所以有可能因为边的不同会出现不同的树,现在如果每条边都有不同的权值,那么最小生成树就是所有树中所有的权值和最小的那个树
- 最小生成树的两种算法
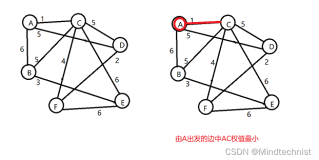
3.1 prim算法
prim算法是通过对点的处理,通过找到一个点,然后再找到另一个点,找另一个点的标准就是这两个点之间边的权值应该最小。
板子
void prim()
{
for(int i=1; i<=n; i++) p[i]=e[1][i],book[i]=0;//先把p数组存入从一点到任一点的距离
book[1]=0;
int u=1;
int num=0;//记录用到了几个点
int sum=0;//记录答案
num++;//第一个点
while(num<n)//当每个点都被连在一起的时候跳出循环
{
int min1=inf;
for(int i=1; i<=n; i++)
{
if(!book[i]&&f[i]<min1) //遍历找到最小的点
{
min1=f[i];
u=i;
}
}
sum=sum+f[i];//记录答案
num++;//记录点
book[u]=1;//标记已经走过
for(int i=1; i<=n; i++)//从上次找到的点相邻的最小边
{
if(!book[i]&&f[i]<e[u][i])
f[i]=e[u][i];
}
}
cout<<sum<<endl;}
3.2 kruskal算法
kruskal和prim可以说恰恰是从另一个角度来考虑这个问题的,首先把所有边摘出来,从小到大排列,每次找边,总是找较小的边,不过如果两个点之间,已经存在直接或者间接相连的边,就不再需要更新这两个点之间的边了,为了实现这个操作就需要用到并查集。这里上代码比较清晰一点
//并查集板子
for(int i=1; i<=n; i++) d[i]=i;//这里是把d数组初始化成1234上升的对应序列
int findx(int x)
{
if(d[x]==x)//如果还是对应相等那么就返回原值
return x;
else//否则就返回这个点的上级
return d[x]=findx(d[x]);//注意这里如果直接返回findx(d[x])而不是返回d[x]=findx(d[x])有时候会报超时(不知道为啥子。。)}
void merge(int x,int y)//查看任意两个点上级是否相等
{
int dx=findx(x);//首先找到这两点的上级
int dy=findx(y);
if(dx!=dy)//判断不相等就让左点变成右点的下级(这里也可以翻着无所谓了)
d[dx]=dy;}
然而完成了这个操作之后还有一步操作紧接着让我们实现,那就是对所有的边进行排序,这里常用的有两种办法
利用结构体排序
struct no
{
int x;//一个点
int y;//另一个点
int v;//两点之间的权值 }e;
bool cmp(no a,no b)
{
return a.v < b.v;//从小到大排序 }
sort(e,e+l,cmp);
void kruskal()
{
int sum=0;//记录走过的权值
int num=0;//记录用到了的点的个数
num++;//第一个点
while(num<n)//(n为点的总个数)
{
}}
利用c++里面的优先队列排序
struct no
{
int x;//一个点
int y;//另一个点
int v;//两点之间的权值 }e;
bool operator <(no a,no b)
{
return a.x > b.x;}
priority_queuequ;
//利用优先队列,将数据存储在队列里面这样每次就会找到最小的边
- 一些模板题
第一题:
poj-1751(highways)
//这个题也是一个标准的kruskal算法
include
include
include
include
using namespace std;
const int inf=1e9;
const int N=10010;
int d[N],xx[N],yy[N];
struct no
{
int x;
int y;
double d;}mp;
bool operator < (no a,no b)
{
return a.d > b.d;}
int findx(int x)
{
if(d[x]==x)
return x;
else
{
d[x]=findx(d[x]);
return d[x];
}// else return findx(d[x]);
}
int merge(int x,int y)
{
int xx=findx(x);
int yy=findx(y);
if(xx!=yy)
{
d[xx]=yy;
return 1;
}
return 0;}
double dmath(int x1,int y1,int x2,int y2)
{
return sqrt(1.0*(x1-x2)*(x1-x2)+1.0*(y1-y2)*(y1-y2));}
int main()
{
int n;
scanf("%d",&n);
priority_queue<no>qu;
for(int i=1; i<=n; i++)
scanf("%d%d",&xx[i],&yy[i]);
for(int i=1; i<n; i++)
for(int j=i+1; j<=n; j++)
{
mp.x=i;
mp.y=j;
mp.d=dmath(xx[i],yy[i],xx[j],yy[j]);// printf("%.2lf \n",mp.d);
qu.push(mp);
}
for(int i=1; i<=n; i++) d[i]=i;
int m;
scanf("%d",&m);
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
merge(a,b);
}
int cut=0;
while(!qu.empty())
{
mp=qu.top();
qu.pop();
if(merge(mp.x,mp.y))
{
cut++;
printf("%d %d\n",mp.x,mp.y);
}
if(cut==n-1) break;
}
return 0; }
第二题:
poj–2349–Arctic Network
这个题就是让你从选中边里面找到一个最长边
include
include
include
include
include
using namespace std;
typedef double dou;
const int N=500+5;
dou d[N];
int xx[N],yy[N];
struct no
{
int x;
int y;
dou d;}mp;
bool operator < (no a,no b)
{
return a.d > b.d;}
dou dmath(dou x1,dou y1,dou x2,dou y2)
{
return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));}
int findx(int x)
{
if(d[x]==x)
return x;
else return findx(d[x]);}
int merge(int x,int y)
{
int t=findx(x);
int l=findx(y);
if(t!=l)
{
d[l]=t;
return 1;
}
return 0;}
int n,s,p;
int main()
{
cin>>n;
while(n--)
{
memset(xx,0,sizeof(xx));
memset(yy,0,sizeof(yy));
priority_queue<no>qu;
cin>>s>>p;
for(int i=1; i<=p; i++)
{
int x,y;
cin>>x>>y;
xx[i]=x;
yy[i]=y;
}
for(int i=1; i<=p; i++)
for(int j=i+1; j<=p; j++)
{
mp.x=i;
mp.y=j;
mp.d=dmath(xx[i],yy[i],xx[j],yy[j]);
qu.push(mp);
}
int l=0;
dou res=-1.0;
for(int i=1; i<=p; i++) d[i]=i;// cout<<qu.size()<<endl;
int k=0;
while(k<p-s)
{
mp=qu.top();
qu.pop();
if(merge(mp.x,mp.y))
{
k++;// printf("%.2lf ",mp.d);
res=max(res,mp.d);
}
}
printf("%.2lf\n",res);
}return 0;
}