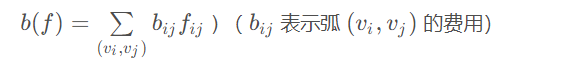/*
poj3422 Kaka's Matrix Travels
不知道 k次 dp做为什么不对???
看了大牛的代码,才知道还可以这样做!
开始没有理解将a 和 a‘ 之间建立怎样的两条边,导致程序一直陷入死循环,真心花了好长时间,快崩溃了。无语.....
题意:有个方阵,每个格子里都有一个非负数,从左上角走到右下角,每次走一步,只能往右或往下走,经过的数字拿走
每次都找可以拿到数字和最大的路径走,走k次,求最大和
这是 最大费用最大流 问题 每次spfa都找的是一条和最大的路径 s--到左上角的边流量是K限制增广次数
求最大费用最大流只需要把费用换成相反数,用最小费用最大流求解即可
构图过程:
每个点拆分成两个 a a' 之间建两条边(当然还要建退边),分别是 (费用为该点相反数,流量为1) (费用为0,流量为k-1)
路过这点时,可以通过前边那条边拿到数字,
以后再从这儿过,就没有数字可拿了,走的就是第二条边
然后是 没点向 右和下 建一条边 费用0,流量k
*/
#include<iostream>
#include<queue>
#include<cstring>
#include<cstdio>
#define N 50000
#define M 5005
#define Max 0x3f3f3f3f
using namespace std;
class EDGE
{
public:
int u, v, c, f;
int next;
};
queue<int>q;
EDGE edge[N];
int cap[55][55], n, k;
int pre[N], first[N];
int dist[M], vis[M];
int edgeN;
int s, t;
int maxFlow;
int spfa()
{
memset(dist, 0x3f, sizeof(dist));
memset(vis, 0, sizeof(vis));
memset(pre, -1, sizeof(pre));
dist[s]=0;
q.push(s);
vis[s]=1;
while(!q.empty())
{
int u=q.front();
q.pop();
vis[u]=0;
for(int e=first[u]; e!=-1; e=edge[e].next)
{
int v=edge[e].v;
if(dist[v]>dist[u] + edge[e].c && edge[e].f>0)
{
dist[v]=dist[u] + edge[e].c;
pre[v]=e;
if(!vis[v])
{
vis[v]=1;
q.push(v);
}
}
}
}
if(dist[t]==Max)
return 0;
return 1;
}
void updateFlow()
{
int minF=Max;
for(int e=pre[t]; e!=-1; e=pre[edge[e].u])
if(minF>edge[e].f)
minF=edge[e].f;
for(int e=pre[t]; e!=-1; e=pre[edge[e].u])
{
edge[e].f-=minF;
edge[e^1].f+=minF;
maxFlow+=minF*edge[e].c;
}
}
void adde(int u, int v, int c, int f)
{
edge[edgeN].u=u; edge[edgeN].v=v;
edge[edgeN].c=c; edge[edgeN].f=f;
edge[edgeN].next=first[u]; first[u]=edgeN++;
edge[edgeN].u=v; edge[edgeN].v=u;
edge[edgeN].c=-c; edge[edgeN].f=0;
edge[edgeN].next=first[v]; first[v]=edgeN++;
}
int main()
{
int i, j;
while(scanf("%d%d", &n, &k)!=EOF)
{
maxFlow=0;
edgeN=0;
memset(first, -1, sizeof(first));
s=0; t=n*n*2+1;
for(i=1; i<=n; ++i)
for(j=1; j<=n; ++j)
scanf("%d", &cap[i][j]);
adde(s, 1, 0, k);
for(i=1; i<=n; ++i)
for(j=1; j<=n; ++j)//n*n个节点,拆点之后变成2*n*n个节点
{
int nb=(i-1)*n+j;
adde(2*nb-1, 2*nb, -cap[i][j], 1);//注意:a到a`是建立两条边,但是两条边的费用和容量不一样
adde(2*nb-1, 2*nb, 0, k-1);
if(j<n)//向右建图
adde(2*nb, 2*(nb+1)-1, 0, k);
if(i<n)//向下建图
adde(2*nb, 2*(nb+n)-1, 0, k);
}
adde(n*n*2, t, 0, k);
while(spfa())//建好图之后,直接调用最小费用最大流模板就好了
updateFlow();
printf("%d\n", -maxFlow);
}
return 0;
}
本文转自 小眼儿 博客园博客,原文链接:http://www.cnblogs.com/hujunzheng/p/3798997.html,如需转载请自行联系原作者