第5章 图的遍历
第1节 深度和广度优先究竟是指啥
深度优先和广度优先其实是针对图的遍历而言的。
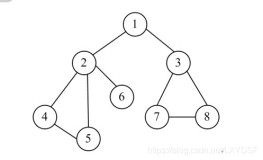
深度优先:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hcM0BPgi-1589449691406)(C:\Users\LF\AppData\Roaming\Typora\typora-user-images\1589015315683.png)]
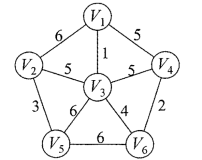
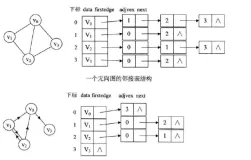
图的存储方法:矩阵存储法
用一个二维数组来存储,第i行第j列代表顶点i到顶点j是否有边,1代表有边,无穷大代表没有边,自己到自己设为0。
//dfs深度优先遍历图 package ch5; import java.util.Scanner; public class Test1 { int []book = new int[101]; int [][]e = new int[101][101]; int sum; int n; void dfs(int cur) { //cur是当前顶点 System.out.print(" "+cur); sum++; if(sum==n) { return; } for(int i=1;i<=n;i++) { if(e[cur][i]==1&&book[i]==0) { book[i]=1; dfs(i); } } return; } public static void main(String[] args) { //图的初始化 Test1 t = new Test1(); Scanner sc = new Scanner(System.in); t.n = sc.nextInt(); for(int i =1;i<=t.n;i++) { for(int j=1;j<=t.n;j++) { if(i==j) { t.e[i][j]=0; }else { t.e[i][j]=999999; } } } int m = sc.nextInt(); for(int i=1;i<=m;i++) { int a = sc.nextInt(); int b = sc.nextInt(); t.e[a][b] = 1; t.e[b][a] = 1; } //从1出发 t.book[1]=1; t.dfs(1); } }
//广度优先遍历图 package ch5; import java.util.Scanner; public class Test2 { public static void main(String[] args) { int []book = new int[101]; int [][]e = new int[101][101]; int sum; int[] que = new int[10001]; int head,tail; //图初始化 Scanner sc = new Scanner(System.in); int n = sc.nextInt(); int m = sc.nextInt(); for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(i==j) { e[i][j]=0; }else { e[i][j]=999999; } } } for(int i=1;i<=m;i++) { int a = sc.nextInt(); int b = sc.nextInt(); e[a][b] = 1; e[b][a] = 1; } //队列初始化 head = 1; tail = 1; //从1号出发 que[tail] = 1; tail++; book[1] = 1; while(head<tail) { int cur = que[head]; for(int i=1;i<=n;i++) { if(e[cur][i] == 1&&book[i]==0) { que[tail] = i; tail++; book[i]=1; } if(tail>n) { break; } } head++; } for(int i=1;i<tail;i++) { System.out.print(" "+que[i]); } } }
第2节 城市地图–图的深度优先遍历
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RiISaMEE-1589449691408)(C:\Users\LF\AppData\Roaming\Typora\typora-user-images\1589165946967.png)]
从1走到5的最短路径
测试数据,测试结果9
5 8 1 2 2 1 5 10 2 3 3 2 5 7 3 1 4 3 4 4 4 5 5 5 3 3
package ch5; import java.util.Scanner; public class Test3 { int []book = new int[101]; int [][]e = new int[101][101]; int n; int min=999999; void dfs(int cur,int dis) { //cur是当前顶点 if(dis>min) { return; } if(cur==n) { if(dis<min) { min = dis; } return ; } for(int i=1;i<=n;i++) { if(e[cur][i]!=999999&&book[i]==0) { book[i]=1; dfs(i,dis+e[cur][i]); book[i]=0; } } return; } public static void main(String[] args) { Test3 t = new Test3(); Scanner sc = new Scanner(System.in); t.n = sc.nextInt(); for(int i =1;i<=t.n;i++) { for(int j=1;j<=t.n;j++) { if(i==j) { t.e[i][j]=0; }else { t.e[i][j]=999999; } } } int m = sc.nextInt(); for(int i=1;i<=m;i++) { int a = sc.nextInt(); int b = sc.nextInt(); int c = sc.nextInt(); t.e[a][b] = c; // t.e[b][a] = c; } //从1出发 t.book[1]=1; t.dfs(1,0); System.out.println(t.min); } }
第3节 最小转机–图的广度优先遍历
5 7 1 5 1 2 1 3 2 3 2 4 3 4 3 5 4 5
package ch5; import java.util.Scanner; public class Test4 { public static class node{ int x; int s; } public static void main(String[] args) { node[] que= new node[2501]; for(int i=0;i<que.length;i++) { que[i] = new node(); } int [][] e = new int [51][51]; int [] book =new int [51]; Scanner sc = new Scanner(System.in); int n = sc.nextInt(); int m = sc.nextInt(); int start = sc.nextInt(); int end = sc.nextInt(); //初始化二维矩阵 for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(i==j) { e[i][j] = 0; }else { e[i][j] = 999999; } } } //读入航班 for(int i=1;i<=m;i++) { int a = sc.nextInt(); int b = sc.nextInt(); e[a][b] = 1; e[b][a] = 1; } ///队列初始化 int head = 1; int tail = 1; que[tail].x = start; que[tail].s = 0; tail++; book[start] =1; //这里书上好像错了 int flag = 0; while(head<tail) { int cur = que[head].x; for(int i=1;i<=n;i++) { if(e[cur][i]!=999999&&book[i]==0) { que[tail].x = i; que[tail].s = que[head].s+1; tail++; book[i] = 1; } if(que[tail].x == end) { flag = 1; break; } } if(flag == 1) { break; } head++; } System.out.println(que[tail-1].s); } }
也可以用深度优先,但广度优先更快,广度优先适合所有边的权值相同的情况。
que[tail].x = i; que[tail].s = que[head].s+1; tail++; book[i] = 1; } if(que[tail].x == end) { flag = 1; break; } } if(flag == 1) { break; } head++; } System.out.println(que[tail-1].s); }
}
也可以用深度优先,但广度优先更快,广度优先适合所有边的权值相同的情况。