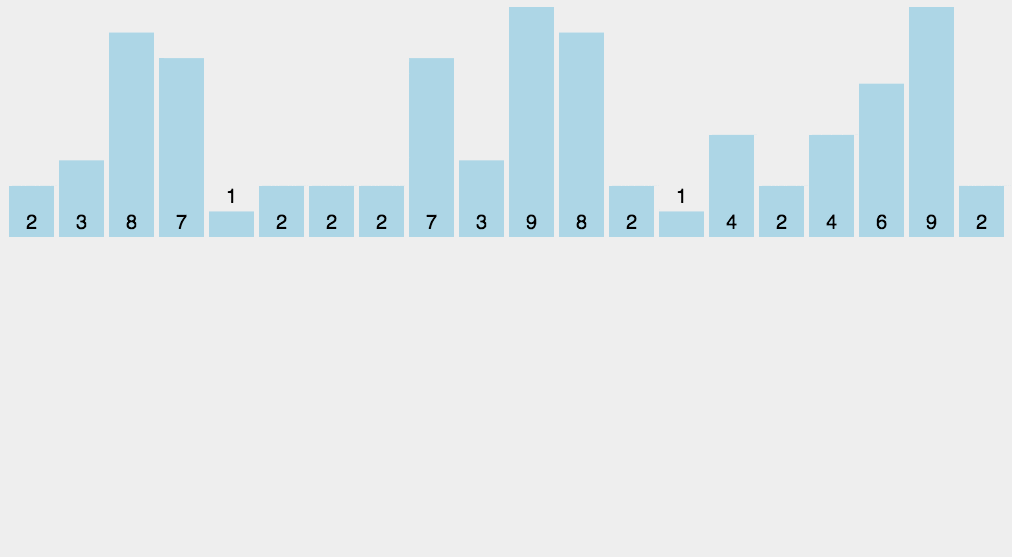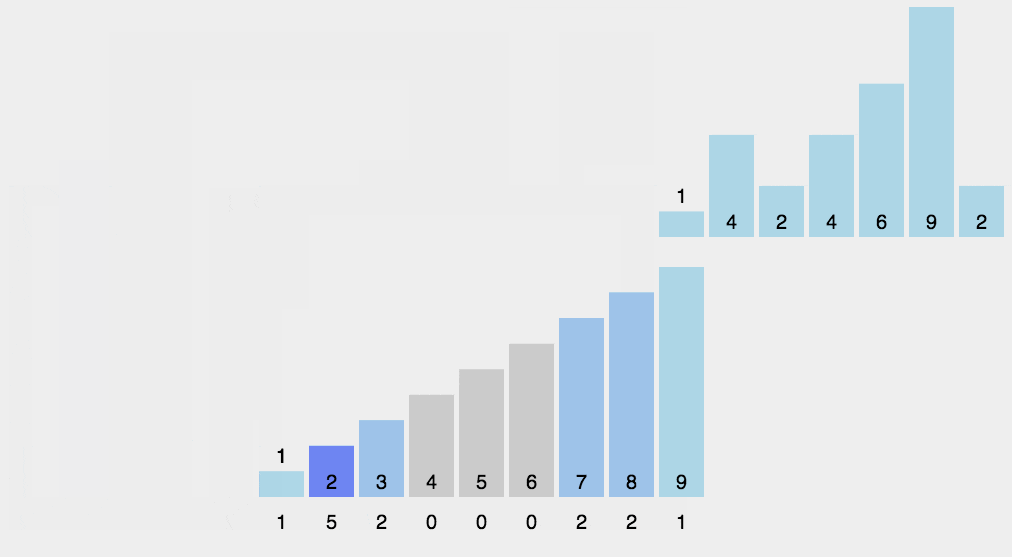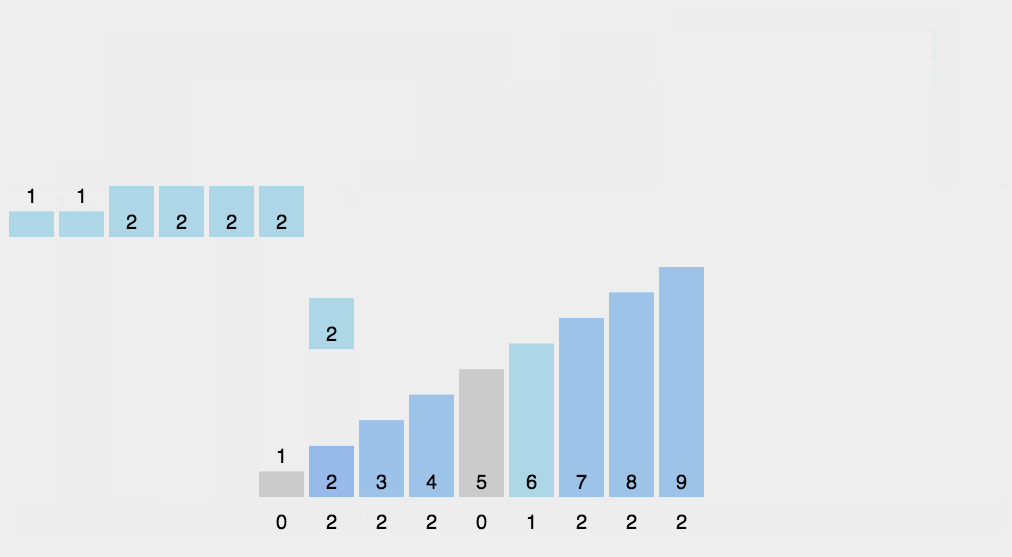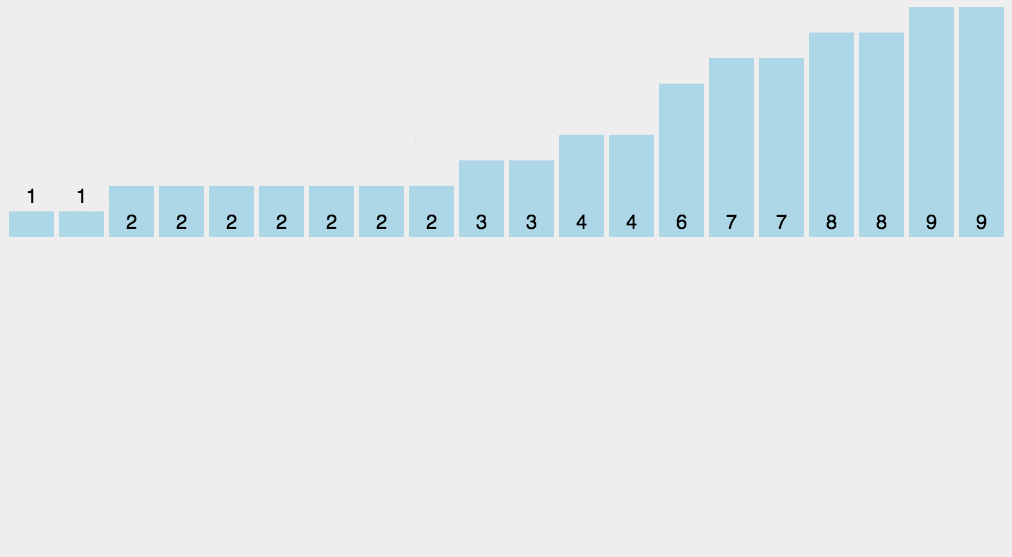百万考生分数如何排序 - 计数排序
关注 「码哥字节」,这里有算法系列、大数据存储系列、Spring 系列、源码架构拆解系列、面试系列……敬请期待。设置星标不迷路
其实计数排序是桶排序的一种特殊情况。桶排序的核心思想是将要排序的数据分到几个有序的桶里,每个桶里的数据再单独进行排序。桶内排完序之后,再把每个桶里的数据按照顺序依次取出,组成的序列就是有序的了。
「码哥字节」之前分享了百万订单如何根据金额排序,就是运用了桶排序。
计数排序的核心在于将输入的数据值转换成键保存在数组下标,所以作为一种线性时间复杂度的排序,输入的数据必须是有确定且范围不大的整数。比如当要排序的 n 个数据,所处的范围不大的时候,最大值是 m,我们就把数据化划分成 m 个桶。每个桶内的数据都是相同的大小,也就不需要桶内排序,这是与桶排序最大的区别。
场景重现
高考查分数系统,系统会展示我们的成绩以及所在省的排名。假如 H 省有 80 万考生,如何通过成绩快速排序得出排名呢?
再比如统计每个省人口的每个年龄人数并且从小到大排序,又如何实现呢?
考生的满分是 750 分,最小是 0 分,符合我们之前说的条件:数据范围小且是整数。我们可以划分为 751 个桶分别对应分数为 0 ~ 750 分数的考生。
接着开始遍历考生数据,每个考生按照分数则划分到对应数组下标,相同数组的下标则将该下标的数据值 + 1。其实就是每个数组下标位置对应的是数列数据出现的次数,最后直接遍历该数组,输出元素的下标就是对应的分数,下标对应的元素值是多少我们就输出几次。
桶内的数据都是分数相同的考生,所以并不需要再进行排序。我们只需要依次扫描每个桶,将桶内的考生依次输出到一个数组中,就实现了 80 万考生的排序。因为只涉及扫描遍历操作,所以时间复杂度是 O(n)。
计数排序的算法思想就是这么简单,跟桶排序非常类似,只是桶的大小粒度不一样。不过,为什么这个排序算法叫“计数”排序呢?“计数”的含义来自哪里呢?
刚刚所说的是朴素版的排序,只是简单的按照统计数组的下标输出元素值,并没有给原始数列进行排序。
在现实中,给学生排序遇到相同分数的就分不清谁是谁?比如并列 95 分的张无忌与周芷若,却不知道是张无忌哪个是周芷若。带着这些问题,请继续看下面的图解思路…...
图解思路
计数统计
为了方便理解,对数据进行简化,假设只有 8 个考生,分数在 0 ~ 5 之间,所以有 5 个桶对应考生分数,值代表每种分数的考生个数。考生的原始数据我们放在数组 SourceArray[8] = {2,5,3,0,2,3,0,3}。
考生的成绩从 0 到 5,使用 大小数组为 6 的 countArray[6] 表示桶,下标对应分数,值存储的是该分数的考生个数。我们只要遍历一遍原始数据就可以得到 countArray[6]。
分数与个数数组
可以知道,分数为 3 分的学生有 3 个, < 3 分的学生有 4 个,所以成绩 = 3 分的学生在排序后的有序数组 sortedArray[8] 中的下标会在 4, 5, 6 的位置,也就是排名是 5,6,7。如下图所示
image
我们如何计算出每个分数的考生在有序数组对应的存储位置呢?这个思路很巧妙,主要是对之前的 countArray[6] 做一下转换。
划重点了同学们:**我们对 countArray[6] 数组顺序求和,countArray[k] 里面存储的是 ≤ k 分数的考生个数 **。这样加的目的是什么?
其实是让统计数组存储的元素值,等于相应考试成绩数据的最终排序位置的序号。
image
现在我就要讲计数排序中最复杂、最难理解的一部分了,坚持啃下来。
- 从后往前遍历原始输入数组 SourceArray[8] = {2,5,3,0,2,3,0,3},扫描成绩为 3 的小强,我们就从 数组 countArray[6] 中取出下标 = 3 的值 = 7,也就意味着包括自己在内,分数 ≤ 3 的考生有 7 位,表示在 sortedArray 中排在第七位,当把小强成绩放到 sortedArray 之后 ≤ 3 的成绩就剩下 6 个了,所以 countArray[3] 要 - 1,变成 6.
- 遍历成绩表倒数第二个数据,成绩是 0,找到在 countArray[0] 的元素 = 2,表示排名第二,同时 countArray[0] 的元素值 -1。
- 以此类推,当扫描完整个原始数组之后, sortedArray 数据就是按照分数从小到大有序排列了。
代码实战
整个步骤:
- 查找数列最大值。
- 根据数列最大值确定 countArray 统计数组长度。
- 遍历原始数据填充统计数组,统计对应元素的个数。
- 统计数组做变形,后面的元素等于前面元素之和。
- 倒序遍历原始数组,从统计数组中找到元素的正确排位,输出到结果数组中。
源码详见 GitHub: https://github.com/UniqueDong/algorithms
package com.zero.algorithms.linear.sort; /** * 公众号:码哥字节 * 计数排序 */ public class CountingSort { public int[] sort(int[] sourceArray) { if (sourceArray == null || sourceArray.length <= 1) { return new int[0]; } // 1.查找数列最大值 int max = sourceArray[0]; for (int value : sourceArray) { max = Math.max(max, value); } // 2.根据数据最大值确定统计数组长度 int[] countArray = new int[max + 1]; // 3. 遍历原始数组映射到统计数组中,统计元素的个数 for (int value : sourceArray) { countArray[value]++; } // 4.统计数组变形,后面的元素等于前面元素之和。目的是定位在结果数组中的排位 for (int i = 1; i <= max; i++) { countArray[i] += countArray[i - 1]; } // 5.倒序遍历原始数组,从统计数组查找对应的正确位置,输出到结果表 int[] sortedArray = new int[sourceArray.length]; for (int i = sourceArray.length - 1; i >= 0; i--) { int value = sourceArray[i]; // 分数在 countArray 中的排名, - 1 则是结果数组的下标 int index = countArray[value] - 1; sortedArray[index] = value; countArray[value]--; } return sortedArray; } }
复杂度分析
第 1、3、5 步都涉及遍历原始数组,时间复杂度都是 O(n),第 4 步统计数组变形,时间复杂度是 O(m),所以总体的时间复杂度是 O(3n +m),去掉系数 O(n) 时间复杂度。
空间复杂度,结果数组 O(n)。
优化思路
前面的代码,第一步我们查找最大值,假如原始数据是 {99,98,92,80,88,87,82,88,99,97,92},最大值是 99,最小值是 80,如果直接创建 100 长度的数组,那么 从 0 到 79 的空间全都浪费了。
要怎么解决呢?
跟着 「码哥字节」来优化,很简单,我们不再使用 max + 1 作为统计数组的长度,而是 max - min + 1 作为统计数组的长度即可。
代码如下:
package com.zero.algorithms.linear.sort; /** * 公众号:码哥字节 * 计数排序 */ public class CountingSort { public int[] sort(int[] sourceArray) { if (sourceArray == null || sourceArray.length <= 1) { return new int[0]; } // 1.查找数列最大值,最小值 int max = sourceArray[0]; int min = sourceArray[0]; for (int value : sourceArray) { max = Math.max(max, value); min = Math.min(min, value); } int d = max - min; // 2.根据数据最大值确定统计数组长度 int[] countArray = new int[d + 1]; // 3. 遍历原始数组映射到统计数组中,统计元素的个数 for (int value : sourceArray) { countArray[value - min]++; } // 4.统计数组变形,后面的元素等于前面元素之和。目的是定位在结果数组中的排位 for (int i = 1; i < countArray.length; i++) { countArray[i] += countArray[i - 1]; } // 5.倒序遍历原始数组,从统计数组查找对应的正确位置,输出到结果表 int[] sortedArray = new int[sourceArray.length]; for (int i = sourceArray.length - 1; i >= 0; i--) { int value = sourceArray[i]; // 分数在 countArray 中的排名, - 1 则是结果数组的下标 int index = countArray[value - min] - 1; sortedArray[index] = value; countArray[value - min]--; } return sortedArray; } }
总结一下
计数排序适用于在数据范围不大的场景中,并且只能给非负整数排序,对于其他类型的数据,要排序的话要在不改变相对大小的情况下,转成非负整数。
比如数据范围 [-1000, 1000] ,就对每个数据 +1000,转换成非负整数。
计数排序这么强大,但是局限性主要有如下两点:
- 当数列的最大与最小值差距过大,不适合使用计数排序。
比如 20 个随机整数,范围在 0 - 1 亿之间,这时候使用计数排序需要创建长度为 1 亿的数组,严重浪费空间。
- 数列元素不是整数,不适合使用
参考资料
极客时间 《数据结构与算法之美》
漫画算法-小灰的算法之旅
关注 「码哥字节」后台回复加群,可添加个人微信进入专属技术群。
码哥字节
读者的分享、点赞、在看、收藏三连是最大的鼓励