一、什么是前后指针法?
前后指针法,顾名思义,就是通过控制两个指针来达到排序的目的的方法。
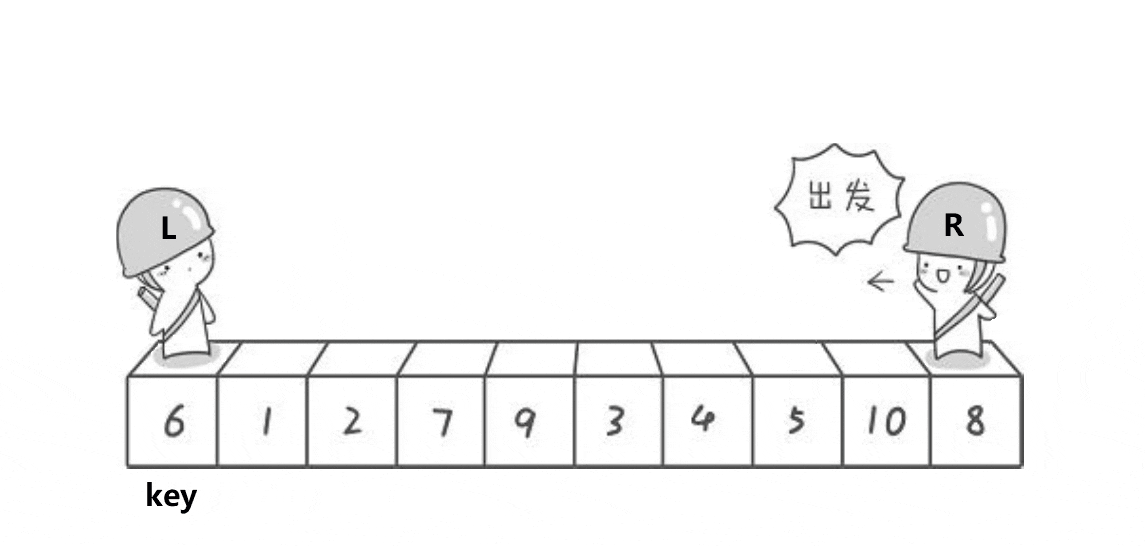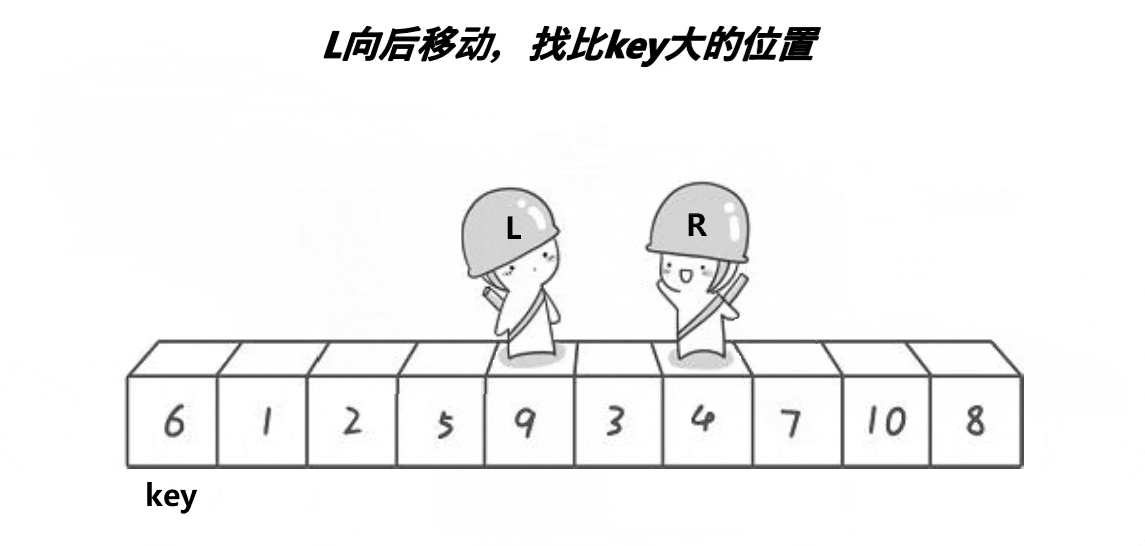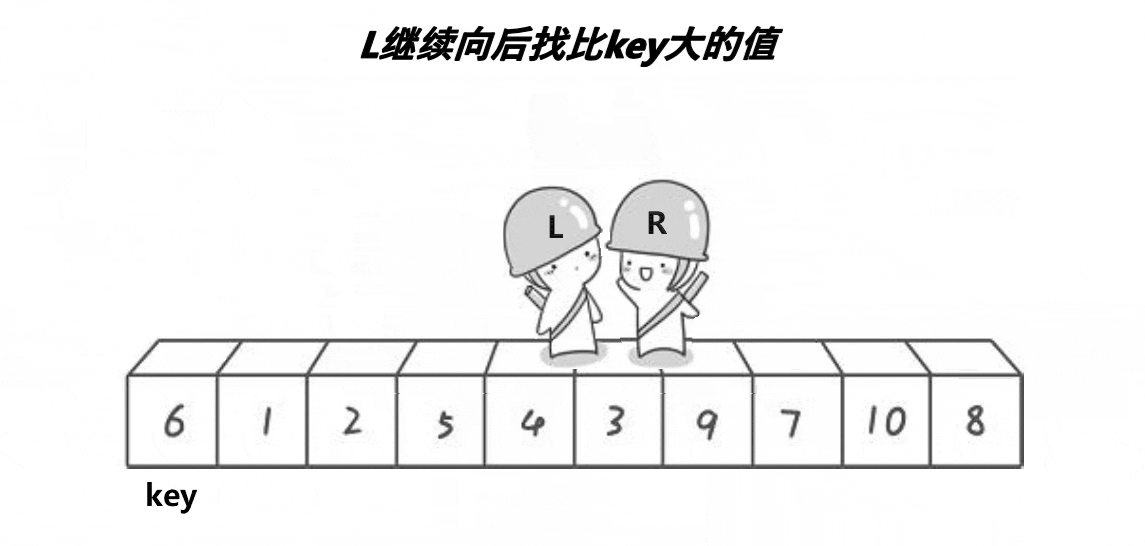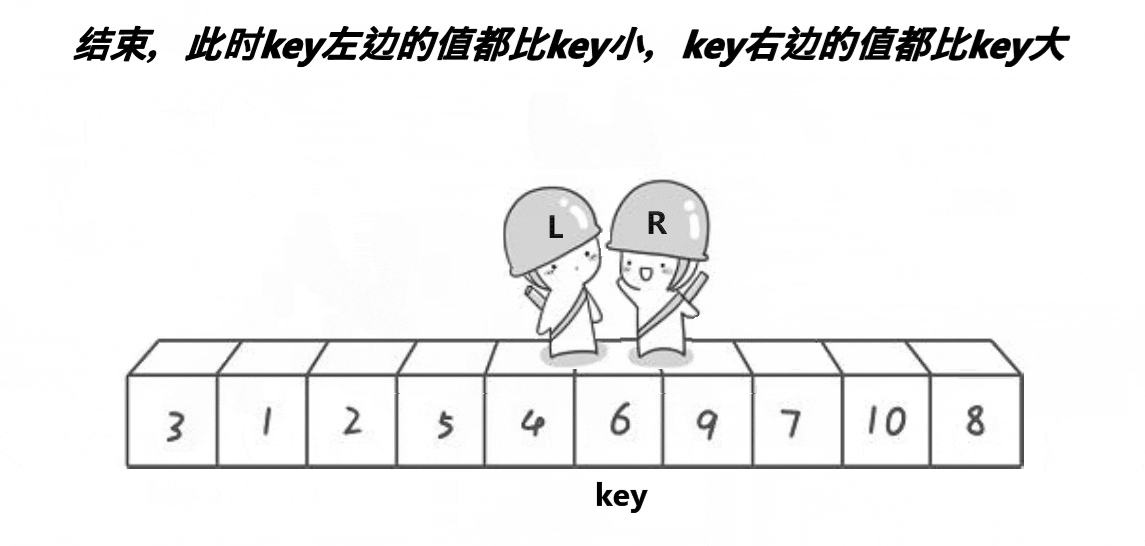
具体思路:先选定左边第一个为基准值key,同时设定left位置为prev,prev的后一个位置为cur,从a[cur]开始和key比较,如果a[cur]比key小,就先将prev++,再让a[cur]和a[prev]交换,然后cur++,如果a[cur]比key大,那么就不改变prev,也不用交换,只对cur++,以此类推,直到cur>right就结束,最后将a[prev]和a[cur]交换就完成了一趟快排。
二、如何用前后指针法实现快速排序?
动图如下:
一趟快排之后得到的结果为:
三、参考代码
//三数取中 int GetMidNumi(int* a, int left, int right) { int mid = (left + right) / 2; if (a[left] > a[mid]) { if (a[mid] > a[right]) { return mid; } //来到这里证明a[mid]最小,那么a[left]和a[right] //谁小谁就是中间的那个数 else if (a[left] < a[right]) { return left; } else { return right; } } else//a[left]<=a[mid] { if (a[mid] < a[right]) { return mid; } //来到这里证明a[mid]最大,那么a[left]和a[right] //谁小谁就是中间的那个数 else if (a[left] < a[right]) { return left; } else { return right; } } } void InsertSort(int* a, int n) { assert(a); int i = 0; int end = 0; int tmp = 0; for (i = 0; i < n - 1; i++) { end = i; tmp = a[end + 1]; while (end >= 0) { if (tmp < a[end]) { a[end + 1] = a[end]; --end; } else { break; } } a[end + 1] = tmp; } } int PartSort3(int* a, int left, int right) { //三数取中 int mid = GetMidNumi(a, left, right); //如果left就是取到的数,那么也就没有必要交换了 if (mid != left) { Swap(&a[left], &a[mid]); } int keyi = left; int prev = left; int cur = prev + 1; while (cur <= right)//由于这里是左闭右闭区间,所以需要取等号 { //这里是逻辑与操作,只有第一个条件成立,第二个条件才会参与判断 //所以后面的++prev是在a[cur]<a[keyi]的条件下再走的,如果++prev //后prev==cur,证明它们的位置是一样的,也就没有必要交换了,只有等 //prev和cur错开才需要交换 if (a[cur] < a[keyi] && (++prev != cur)) { Swap(&a[cur], &a[prev]); } //无论上面是否需要交换,cur都需要++ cur++; } //最后prev的位置就是a[keyi]的最终的位置,交换prev和keyi对应的值 Swap(&a[prev], &a[keyi]); //交换后a[prev]的值比前面的值大,比后面的值小,这里就是分界点,返回这个prev做递归的边界 return prev; } void QuickSort(int* a, int left,int right) { assert(a); //区间只有一个值或者区间不存在就不用再递归下去了 if (left >= right) { return; } //这里进行一个小区间优化,当一个区间<=10个元素的时候 //快排已经不再适合,因为快排是数据越多并且越乱的时候 //才是越快的,但是数据量小的时候,快排是没有很大的优势 // 的如果这个是一个大数组经过多次递归下来的小区间,证明 // 这个区间接近于有序的,此时换成直接插入排序会更加的高效 if (right - left + 1 < 10) { InsertSort(a + left, right + 1 - left); } else { //每一趟快排之后都返回keyi的位置,把区间分成 //[left,keyi-1][keyi][keyi+1,right]三个部分 //再对子区间的数组进行快排,直到不满足递归条件再返回 int keyi = PartSort3(a, left, right); QuickSort(a, left, keyi - 1); QuickSort(a, keyi + 1, right); } }
四、时间复杂度
快排的三个时间复杂度其实都是一样的O(N*logN),因为三种方法在思想上没有什么区别,只是在实现上略有差异。证明如下: