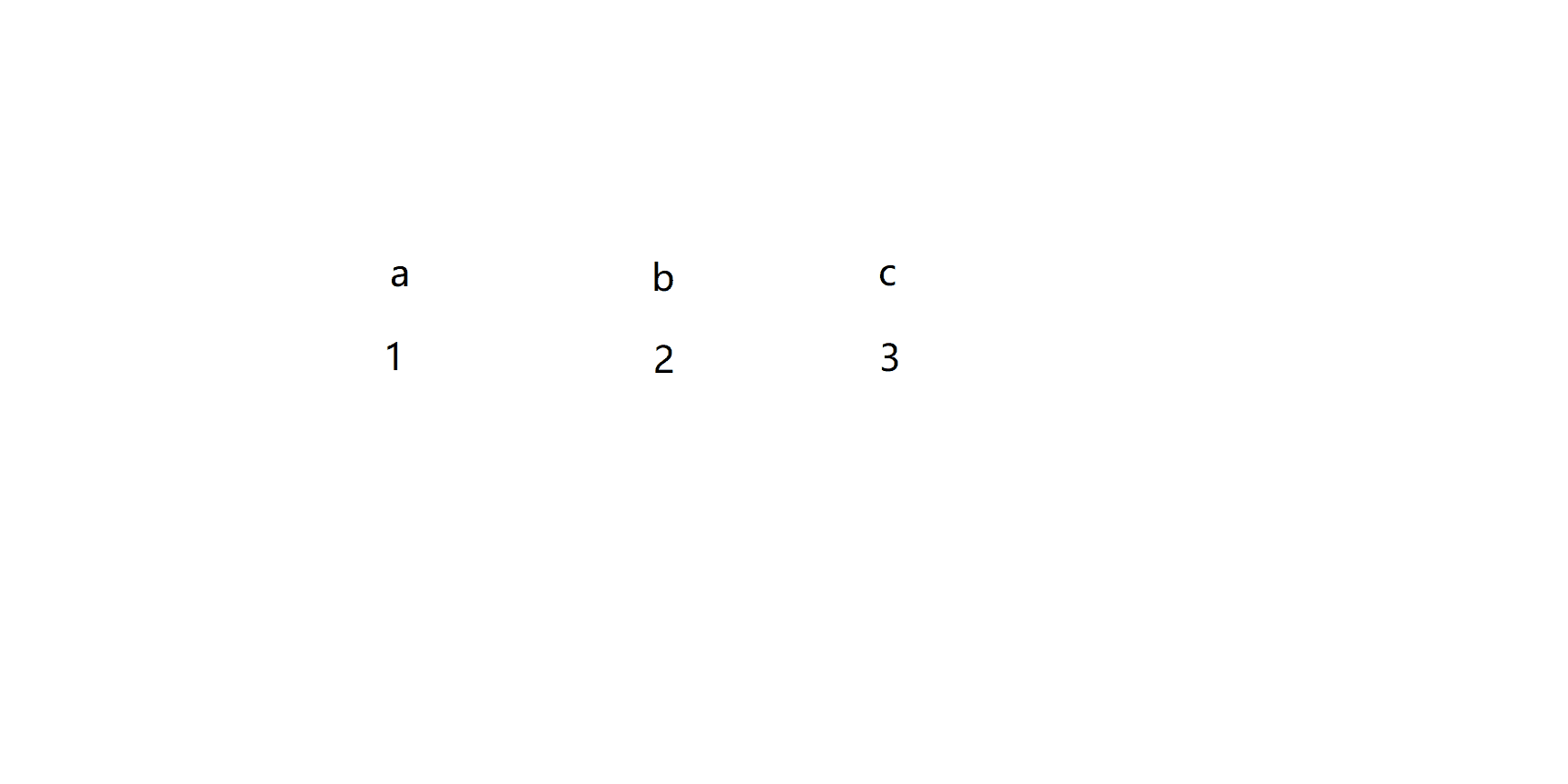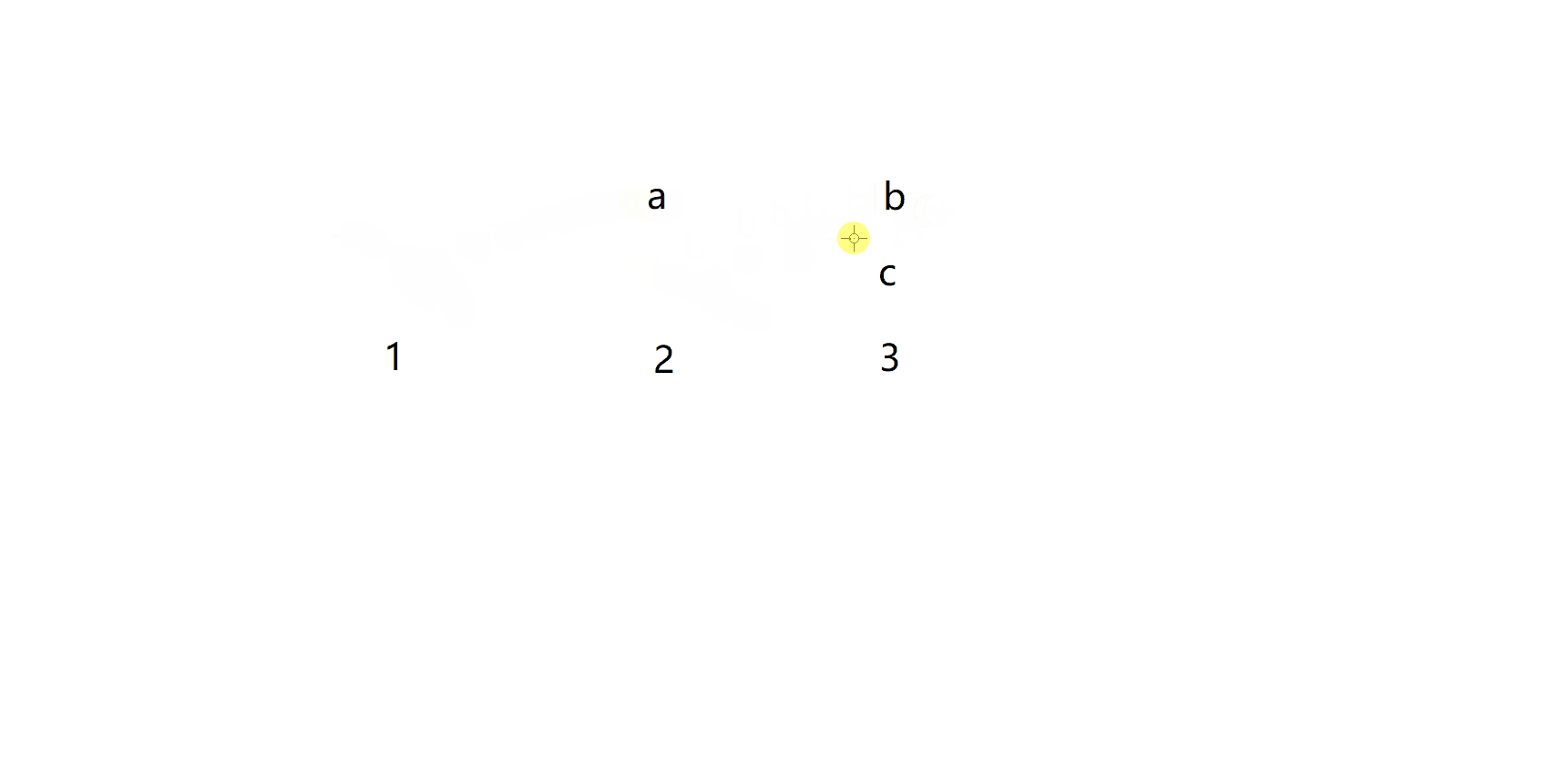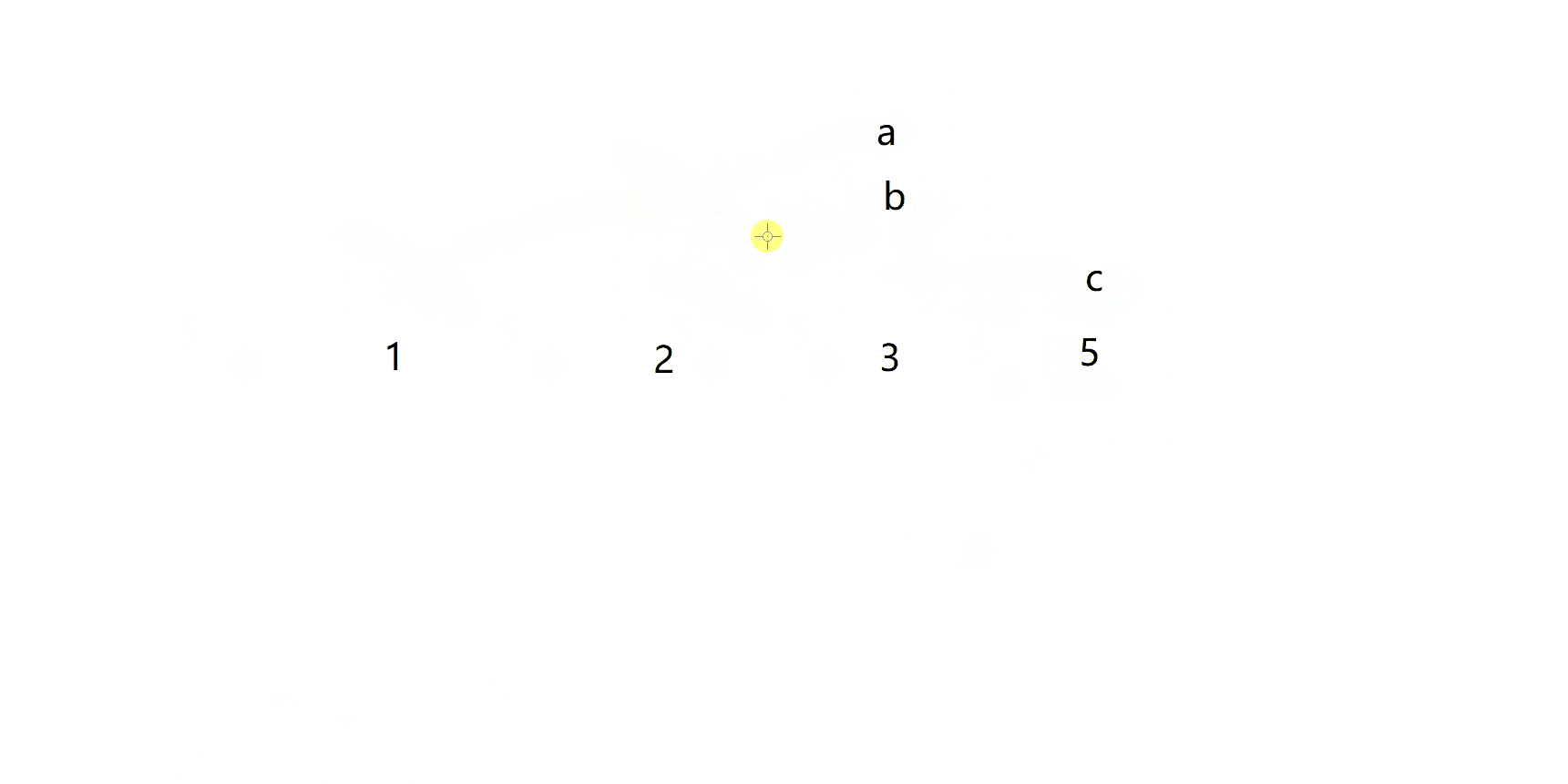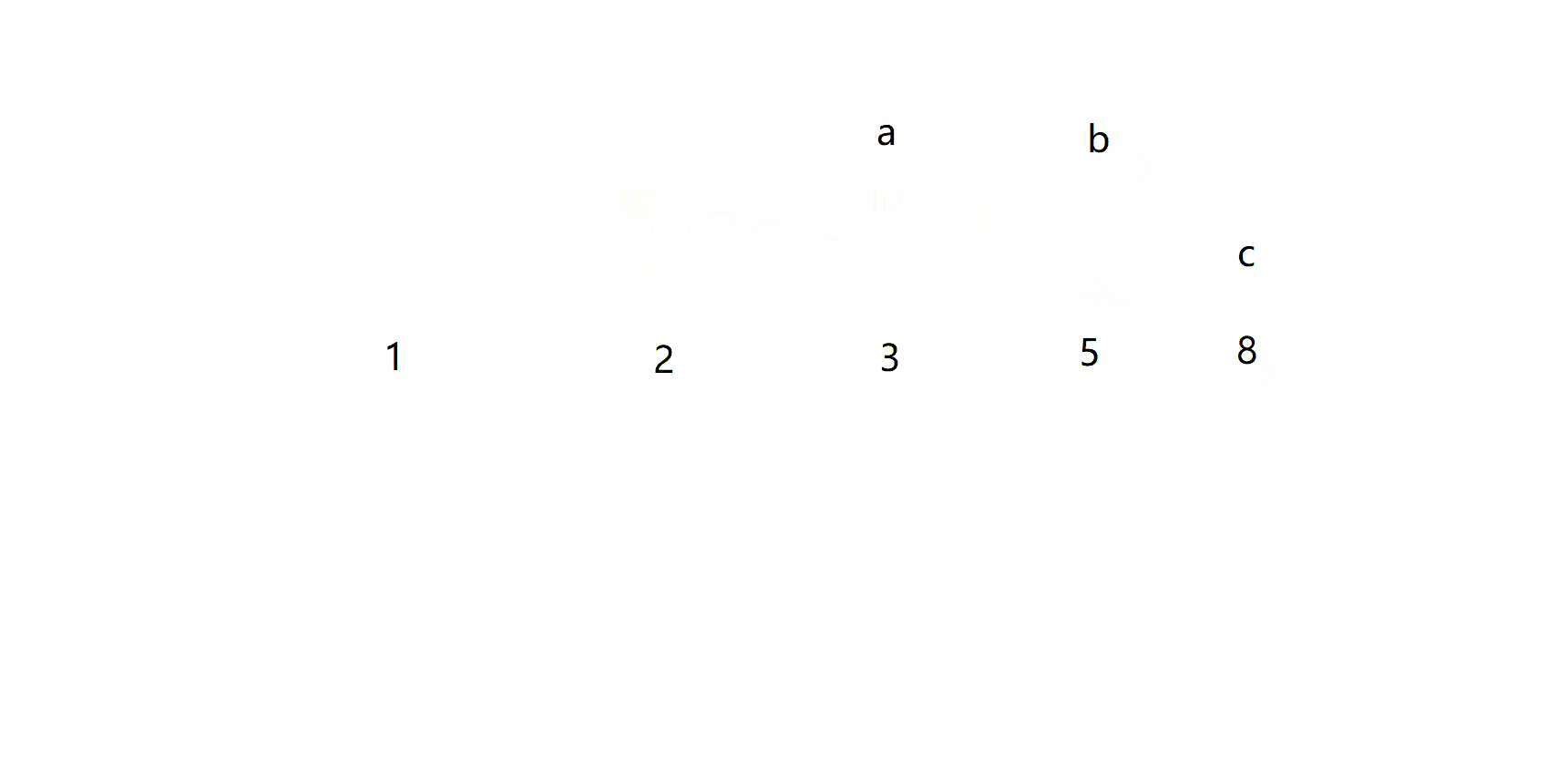青蛙跳台阶问题
题目描述
问题分析
递归解法
非递归解法
题目描述
一只青蛙可以一次跳1级台阶或一次跳2级台阶,例如:跳上第一级台阶只有一种跳法:直接跳1级即可。跳上两级台阶,有两种跳法:每次跳1级,跳两次;或者一次跳2级.问要跳上第级台阶有多少种跳法?
问题分析
有一个台阶时:青蛙只能一级台阶,跳法一种
有2个台阶时:青蛙可以一次跳2级台阶,也可以跳2次一级台阶,所以跳法两种:
当有三级台阶时,如果青蛙第一次跳一级台阶,那么之后它就有两级台阶需要跳;如果第一次跳2级台阶,那么那之后就有1级台阶需要跳。这就把问题抛到了跳一级台阶和跳两级台阶的问题上,所以有3种跳法
第一次跳1级:
第一次跳2级:
所以,当有n级台阶时,就可以把问题抛到n-1级台阶和n-2级台阶问题中,而这两个问题还可以细分,所以我们自然而然容易想到递归
第一次跳1级:
第一次跳2级:
设跳n级台阶跳法为f(n)次
n = 1时,f(n) = 1;
n = 2时,f(n) = 2;
n>=3时,f(n) = f(n-1)+f(n-2);
递归解法
代码:
#include <stdio.h> int times(int n) { if (n == 1) { return 1; } else if (n ==2) { return 2; } else { return times(n - 1) + times(n - 2); } } int main() { int n = 0; scanf("%d", &n); int time = times(n); printf("跳%d个台阶,需要%d次\n", n, time); return 0; }
非递归解法
在前面的分析可以发现,n>=3时,f(n) = f(n-1)+f(n-2),也就是前n阶的前两种情况
所以完全可以使用非递归的循环语句解决这个问题
int times2(int n) { if (n == 1) { return 1; } if (n == 2) { return 2; } else { int a = 1; //一阶台阶有1中跳法 int b = 2; //二阶台阶有2种跳法 int c = 0; while (n > 2) { c = a + b; a = b; b = c; n--; } return c; } } int main() { int n = 0; scanf("%d", &n); int time2 = times2(n); printf("跳%d个台阶,需要%d次\n", n, time2); return 0; }
这里用动图解释过程
全部代码
#include <stdio.h> int times(int n) { if (n == 1) { return 1; } else if (n ==2) { return 2; } else { return times(n - 1) + times(n - 2); } } int times2(int n) { if (n == 1) { return 1; } if (n == 2) { return 2; } else { int a = 1; int b = 2; int c = 0; while (n > 2) { c = a + b; a = b; b = c; n--; } return c; } } int main() { int n = 0; scanf("%d", &n); int time = times(n); printf("递归:跳%d个台阶,需要%d次\n", n, time); int time2 = times2(n); printf("非递归:跳%d个台阶,需要%d次\n", n, time2); return 0; }
测试结果:
——————————————