1.实验目的
(1)掌握贪心算法的处理思路与算法框架。
(2)掌握应用贪心算法解决具体问题的方法。
(3)掌握贪心算法的广泛应用。
2.实验内容
(1)问题描述
(2)输入
(3)输出
输出只有一行。
输出剩下的新数字,这个数字最小。
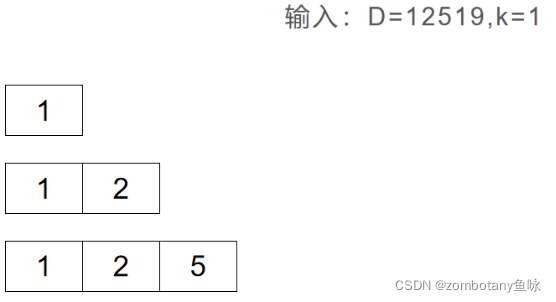
3.问题实例分析
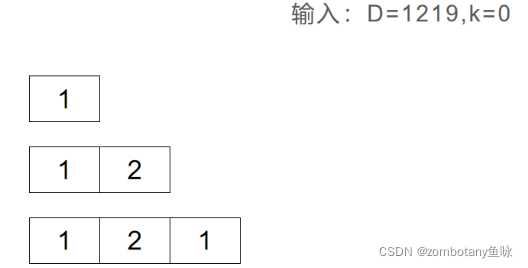
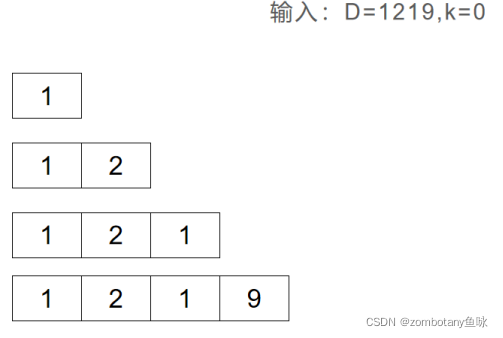
在本问题实例中还未覆盖如下两种情况。
初始时,将1和4入栈。3<4,则3入栈,4出栈,把4删除。
3入栈后,1<3.下一位数字为2,2<3。所以,需要将3出栈,并删除3。
1入栈后,尽管2>1,但是此时删除数字的次数已经被用光了,所以不能将2出栈并删除,而是将剩下的数字全部直接入栈。
4.算法描述及说明
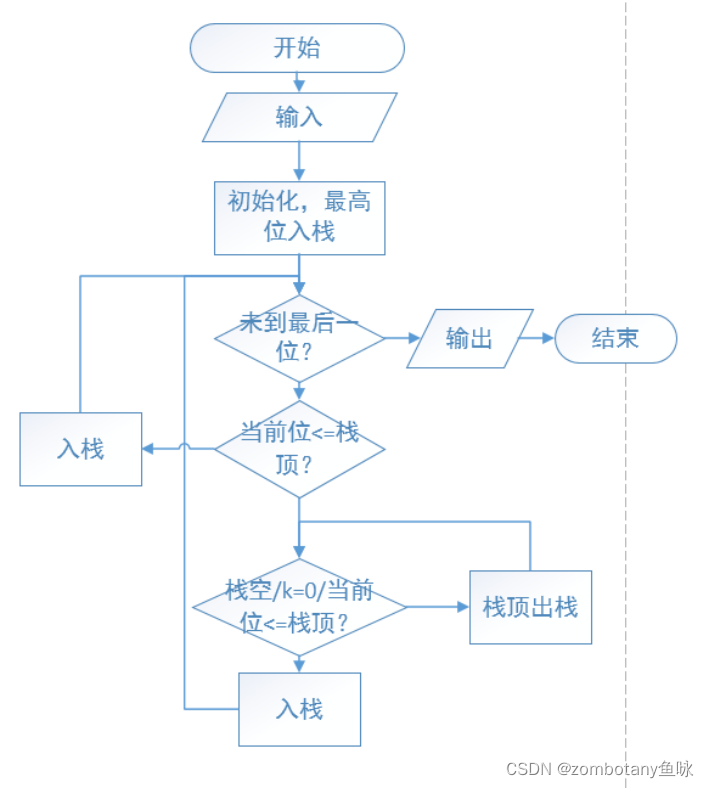
正如第3节问题实例分析所述,算法的整体流程如下:
1.输入数据,这个数据用数组的形式进行存储,数组的每一位表示原数字的每一位。
2.创建一个栈,将最高位数入栈。
3.遍历数字的每一位,若当前位数字小于栈顶元素,则将栈顶的数出栈并删除。直到栈为空,或k kk个数字的删除次数被用完,或直到新的栈顶元素小于等于当前位数字。
4.特判特殊情况:删掉过m个数字且m<k,则需要删除最后的k−m位数字。
5.将删完后的新数字进行输出。
5.算法正确性分析
6.算法时间复杂性分析
7.运行结果展示及其说明
测试样例使用了两组。对于每一组测试样例,都能正确地根据数字的位数n、数值D要删除的位数k生成数值最小的新数。
8.心得体会
9.程序源代码
#include<iostream> #include<cstring> #include<cmath> #include<vector> int d[20];//一个数最多18位 using namespace std; int main() { int n,k; long long D; cin >> n; cin >> D; cin >> k; long long temp = D; for (int i = n; i >= 1; i--) { d[i] = temp % 10; temp = temp / 10; } vector<int> stk; for (int i = 1; i <= n; i++) { while (stk.size() > 0 && stk.back() > d[i] && k > 0) { k--; stk.pop_back(); } stk.push_back(d[i]); } for (; k > 0; k--) stk.pop_back(); long long ans = 0;//新数字 for (int i = 0; i < stk.size(); i++) { ans = ans * 10; ans += stk[i]; } cout << ans; return 0; }