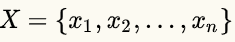2.2.5 带截距的线性方程
2.2.5.1 增加截距 12
🚩上述八元一次方程的解其实就是:
y = y + 12 display(y) model = LinearRegression(fit_intercept = True) # fit:健身,训练;特质算法、模型训练,拟合 # 数据 X 和 y 之间存在规律,拟合出来,找到规律 model.fit(X, y) b_ = model.intercept_ print('截距是:', b_) w_ = model.coef_ print('斜率是:', w_) print('方程的解为:', X.dot(w_) + b_)
我们可以看出,求出来的截距虽然不是我们加上的 12,斜率也不是我们之前求过的解,但是这两个结合起来确确实实是方程的解。
求出的不是我们期望的结果,但是是符合题意的结果,这是因为,一旦我们规定了 fit_intercept = True,那么在计算机进行解方程的时候,就不会使用正规方程去进行运算
2.2.5.2 修改数据 X
🚩我们根据 1.5 多元线性回归 所讲过的对X进行修改:即给X所代表的矩阵中在最后一列的位置增加一个-1:
X = np.concatenate([X, np.full(shape = (8, 1), fill_value = 1)], axis = 1) display(X, y)
那么这个数据,相比较与最开始的八元一次方程,我们让 X 增加了一列,y 增加了 12 ,那么接下来进行正规方程的计算:
model = LinearRegression(fit_intercept = False) model.fit(X, y) display(model.coef_, model.intercept_)
W = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y) W
可以看出即使是使用我们推导出的正规方程也和我们期待的相差甚远,我们来查看一下此时的X
X.shape
这意味着,我们有八个方程,但是我们有九个未知数,显然,对于这样的一个方程组,我们并非只有一组解,而是有无穷多组解,这也是我们产生偏差的原因。
你或许有疑问,既然有无穷多组解,那么每次运行的结果应该是不同的,为什么对于正规方程每次运行的结果确实相同的:这是因为算法会默认给我们算出一个 最优解,所以我们要有唯一解,就需要我们人为的添加一个方程:
# w就是标准的解 w = np.array([ 1., 5., 15., 3., 8., 4., 17., 12.]) # 造一个方程出来 X9 = np.random.randint(-15, 15, size = 8) display(X9)
接下来对于这个方程我们按照增加 12 截距和修改数据的方法来改变这个方程:
# 上面的8个方程,都有截距12,第九个方程也是如此 X9.dot(w) + 12
y = np.concatenate([y, [X9.dot(w) + 12]]) y
X9 = np.concatenate([X9, [1]]) X9
X = np.concatenate([X, [X9]]) X
以上操作后我们就处理好了 X 和 y ,那么接下来,就是见证奇迹的时刻:
# 计算正规方程 np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
使用线性回归:
model = LinearRegression(fit_intercept = False) model.fit(X, y) display(model.coef_)
那么这还是有些区别,因为我们想要的是截距以及斜率,但是此时我们只有斜率,故我们可以把 fit_intercept 设置为 True:
model = LinearRegression(fit_intercept = True) model.fit(X, y) display(model.coef_, model.intercept_)
截距是不是离我们的真实值特别靠近啦,此时我们只需要进行四舍五入即可,对于值为 0 的解,即我们自定义出来的 X 9 ,0 代表其没有权重,故我们可以舍去它
model = LinearRegression(fit_intercept = True) model.fit(X[:,:-1], y) display(model.coef_, model.intercept_.round())
芜湖!大功告成!!!
2.3 矩阵转置公式与求导公式
转置公式如下:
求导公式如下:
2.4 推导正规方程 θ 的解
- 矩阵乘法公式展开
- 进行求导(注意X、y是已知量,θ \thetaθ 是未知数):
- 根据上面求导公式进行运算:
- 令导数J ′ ( θ ) = 0 :
- 矩阵没有除法,使用逆矩阵进行转化:
到此为止,公式推导出来了~
2.5 凸函数判定
🚩判定损失函数是凸函数的好处在于我们可能很肯定的知道我们求得的极值即最优解,一定是全局最优解。
如果是非凸函数,那就不一定可以获取全局最优解,如下图:
来一个更加立体的效果图:
判定凸函数的方式: 判定凸函数的方式非常多,其中一个方法是看 黑塞矩阵 是否是 半正定 的。