拉格朗日中值定理又称拉氏定理,是微分学中的基本定理之一,它反映了可导函数在闭区间上的整体的平均变化率与区间内某点的局部变化率的关系。拉格朗日中值定理是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形,是泰勒公式的弱形式。
拉格朗日中值定理表述如下:
如果函数f(x)满足:
(1) 在闭区间[a,b]上连续;
(2) 在开区间(a,b)内可导;
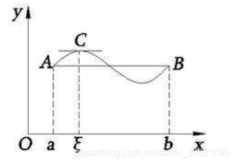
那么在开区间(a,b)内至少有一点ε(a<ε<b)使等式f(b)−f(a)=f′(ε)(b−a)成立。
精彩的大学生活体现在高等数学中,拉格朗日中值定理也是快乐的源泉之一。
小周在学这个定理的时候意识到虽然这个定理很漂亮,但是这个点ε其实并不好找,于是向高数成绩特别好的你求助。
输入格式:
输入在一行中给出两个整数,分别为a和b。其中,a表示区间的左端点,b表示区间的右端点。
题目保证整数a,b均在int类型可表示范围内。
输出格式:
在一行中输出点ε的值。结果保留1位小数。
为了方便你研究这个问题,小周贴心地令 f(x)=x2 ,然后只告诉你a与b的值(a,b即为区间的左、右端点),你只需将点ε求出后输出即可。
输入样例:
1 3
输出样例:
2.0
样例解释:
将a=1,b=3代入方程f(b)−f(a)=f′(ε)(b−a),有32−12=2∗ε∗(3−1)⇒8=4∗ε⇒ε=2.0,即ε=2.0
#include<iostream> using namespace std; int main() { int a,b; cin>>a>>b; double c; c=(b*b-a*a)*1.0/2/(b-a); printf("%.1f",c); }