概述
降维是机器学习中十分重要的一种思想。在机器学习中,我们会经常处理一些高维数据,而高维数据情形下,会出现距离计算困难,数据样本稀疏等问题。这类问题是所有机器学习方法共同面临的问题,我们也称之为“维度灾难”。在高维特征中,也容易出现特征之间存在线性相关,也就是说有的特征是冗余的,因此降维也是必要的。
降维的优点(必要性):
- 去除噪声
- 降低算法的计算开销(改善模型的性能)
- 使得数据更容易使用
- 使得数据更容易理解(几百个维度难以理解,几个维度可视化易理解)
降维的方法有很多,主要分为两大类:
线性降维:PCA,LDA,SVD等
非线性降维:核方法(核+线性),二维化和张量化(二维+线性),流形学习(ISOMap,LLE,LPP)等
下面我们主要学习一下PCA降维算法。
1. 什么是降维?
降维,简单来说就是尽量保证数据本质的前提下将数据维数降低。降维可以理解为一种映射关系,例如函数z = f(x,y),可以二维转为一维。
2.什么是PCA?
PCA:principal component analysis,主成分分析,
是一种广泛用于数据压缩的算法(常用的降维技术)。PCA的思想是将n维特征映射到k维,这k维特征是全新的正交特征。这k维特征称为主元,是重新构造出来的特征。在PCA中,数据从原来的坐标系转换到新的坐标系下,新的坐标系的选择与数据本身决定。其中,第一个新坐标轴选择的是原始数据中方差最大的方向,第二个新坐标轴选取的是与第一个坐标轴正交且具有最大方差的方向,依次类推,我们可以取到这样的k个坐标轴,从而构造出k个特征。
3.PCA的操作步骤
(1)去平均值,即每一维特征减去各自的平均值
(2)计算协方差矩阵
(3)计算协方差矩阵的特征值与特征向量
(4)对特征值从大到小排序
(5)保留最大的k个特征向量
(6)将数据转换到k个特征向量构建的新空间中
具体实例:
(我们先用矩阵利器matlab工具做)
我们现在有二维数组:==dataSet==,10行2列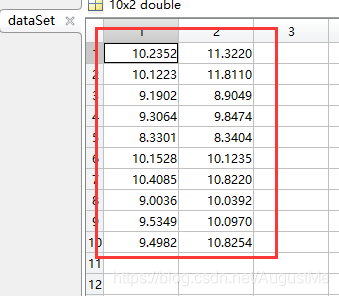
这个数据我们可以自己做,手动输入到txt文档里就可以了。
10行2列的数据,求每一维(每一列的数据均值):==dataSetMean==,1行2列
然后,原始数据每一维上的数据减去各自的均值得到==dataSetAdjust==,10行2列
计算dataSetAdjust的协方差矩阵(怎么计算一个矩阵的协方差矩阵?请点这里),得到==dataCov==,2行2列
求协方差矩阵的特征值和特征向量(怎么计算特征值和特征向量?清点这里):
特征值:D
特征向量:V
接着,对特征值进行排序,2维降1维,显然1.4214>0.1120
我们选择第二个特征值对应的特征向量:V_
转换到新的空间得到降维后的数据:==FinalData==,10行1列
dataSetAdjust * V_ , 
这样,我们就完成了,将10 × 2降维到10 × 1(2维降到1维)。
pca_SampleData_matlab.m
clc;clear
%% 导入数据
dataSet = load('data/SampleData.txt');
% pca
k = 1; % 目标维数
[FinalData, reconData] = PCA(dataSet, k);
%% 作图
hold on
plot(dataSet(:,1), dataSet(:,2), '.');
plot(reconData(:,1), reconData(:,2), '.r');
hold offPCA.m
function [ FinalData,reconData ] = PCA( dataSet, k )
[m,n] = size(dataSet);
%% 去除平均值
%取平均值
dataSetMean = mean(dataSet);
%减去平均值
dataSetAdjust = zeros(m,n);
for i = 1 : m
dataSetAdjust(i , :) = dataSet(i , :) - dataSetMean;
end
%% 计算协方差矩阵
dataCov = cov(dataSetAdjust);
%% 计算协方差矩阵的特征值与特征向量
[V, D] = eig(dataCov);
% 将特征值矩阵转换成向量
d = zeros(1, n);
for i = 1:n
d(1,i) = D(i,i);
end
%% 对特征值排序
[maxD, index] = sort(d);
%% 选取前k个最大的特征值
% maxD_k = maxD(1, (n-k+1):n);
index_k = index(1, (n-k+1):n);
% 对应的特征向量
V_k = zeros(n,k);
for i = 1:k
V_k(:,i) = V(:,index_k(1,i));
end
%% 转换到新的空间
FinalData = dataSetAdjust*V_k;
% 在原图中找到这些点, 数据还原
reconData = FinalData * V_k';
for i = 1 : m
reconData(i , :) = reconData(i , :) + dataSetMean;
end
end(我们用python做)
python3代码实现:
# -*- coding: utf-8 -*-
import numpy as np
#计算均值,要求输入数据为numpy的矩阵格式,行表示样本数,列表示特征
def meanX(dataX):
return np.mean(dataX,axis=0)#axis=0表示按照列来求均值,如果输入list,则axis=1
def pca(XMat, k):
average = meanX(XMat)
m, n = np.shape(XMat)
avgs = np.tile(average, (m, 1))
data_adjust = XMat - avgs
covX = np.cov(data_adjust.T) #计算协方差矩阵
featValue, featVec= np.linalg.eig(covX) #求解协方差矩阵的特征值和特征向量
index = np.argsort(-featValue) #按照featValue进行从大到小排序
if k > n:
print ("k must lower than feature number")
return
else:
#注意特征向量是列向量,而numpy的二维矩阵(数组)a[m][n]中,a[1]表示第1行值
selectVec = np.matrix(featVec.T[index[:k]]) #所以这里需要进行转置
finalData = data_adjust * selectVec.T
reconData = (finalData * selectVec) + average
return finalData, reconData
#根据数据集data.txt
def main():
XMat = np.loadtxt("data/SampleData.txt")
k = 1 # 目标维数
return pca(XMat, k)
if __name__ == "__main__":
finalData, reconMat = main() 我们依次查看运行过程求解得到的变量:
原始数据(待降维的数据集),XMat:
每列特征均值:average:
原始数据集每一维特征减去均值average,得到data_adjust:
计算data_adjust矩阵的协方差矩阵,得到covX矩阵:
计算协方差矩阵的特征值和特征向量:
特征值,feaValue:
特征向量,feaVec:
对特征值进行排序,从大到小,选取前k个特征值对应的特征向量,我们的例子是二维降一维,只需要选最大的特征值对应的特征向量(selectVec)即可,很显然是上述矩阵的第二列。
转换到新空间:
finalData = data_adjust * selectVec.T 
python直接调用PCA模块实现:
from sklearn.decomposition import PCA
import numpy as np
datas = np.loadtxt('data/SampleData.txt') # 原始数据
pca = PCA(n_components=1) # 加载PCA算法,设置降维后主成分数目为1
datas_pca = pca.fit_transform(datas) # 对样本进行降维,data_pca降维后的数据run result: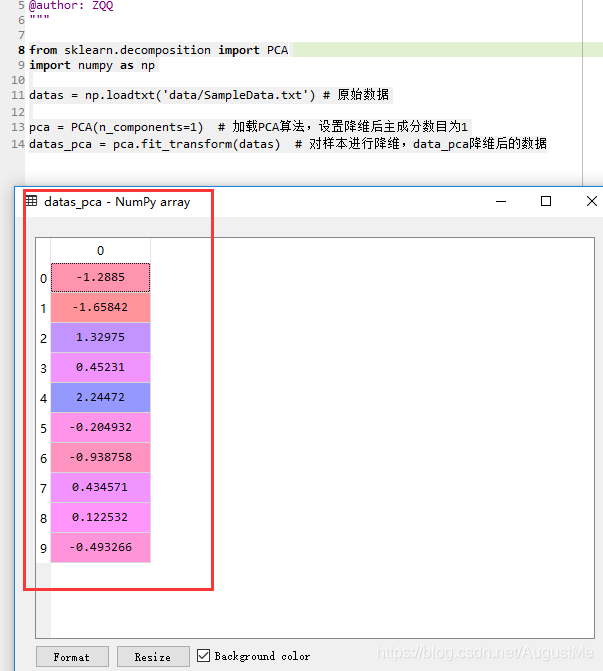
这样太方便了,感觉走上了人生巅峰!!!(我们最好在明白原理,计算步骤的情况下使用,莫要成为一名调包侠啦,哈哈)
注:发现一个问题,matlab降维和python降维结果不相同啊!它们的结果相差一个==负号==
这个并不影响后面的计算。
实际上,都是对的,为什么这么说呢?
仔细阅读你会发现,matlab和python在计算特征向量的过程中出现了差异,也就是出现了正负号的问题,第二个特征向量用matlab和python计算时,正负号不同啦。
出现的原因是什么呢?如果你学过线性代数,你会知道,一个矩阵A对应的特征值是不变的,特征值对应着特征向量,这个向量是一个通解(参数取值不同,会改变),k*p + C, 其中k和C是常数,而p是特征值对应的基础解系。因此,在matlab和python中出现正负号的原因,是常数的取值不同,比如说,matlab中,k默认取+1,C取0,而python中k默认取-1,C取0。因此,最终的结果,是正负号不同。
我们也可以这样理解,n维特征映射到k维,映射的方向不同(投影的方向),则出现结果符号(正负号)的差异。
如果你不是很懂,可以看我的关于求解矩阵特征值和特征向量的文章(请点这里)。
以上,是我们的个人理解,仅做参考,新手上路,勿喷啊,有错的的地方,请指正。
总结:PCA技术的一个很大的优点是,它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。
但是,这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高。
如果后期有空,源代码放github上,供需要的人免费使用,喜欢的给我点个star,谢谢。
参考和引用:
https://www.cnblogs.com/guoyaohua/p/8855636.html
https://www.cnblogs.com/jiangxinyang/p/9291741.html
https://www.cnblogs.com/zy230530/p/7074215.html
https://blog.csdn.net/google19890102/article/details/27969459
仅用来个人学习和分享,如若侵权,留言立删。