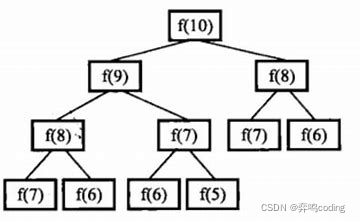
在使用递归来求斐波那契数列时,可以发现,在这个过程中我们重复计算了一些值,如下图所示,很多值都计算过了,但在递归过程我们没有做其他的操作,所以就只能重复的算下去,那如果我们将计算的值保存下来,在进行递归时能够查找到计算过的值,就直接调用而不用重复的计算了
先来看初级版
public class Test3 { public static void main(String[] args) { long startTime = System.nanoTime(); //获取开始时间 int a = fib(20); System.out.println(a); long endTime = System.nanoTime(); //获取结束时间 System.out.println("time:" + (endTime - startTime) + "ns"); //输出程序运行时间 } private static Integer fib(int n){ if (n==0)return 0; if (n==1||n==2)return 1; return fib(n-1)+fib(n-2); } }
然后测个速,我这里用的纳秒
进阶版
import java.util.*; public class Test1 { public static void main(String[] args) { long startTime = System.nanoTime(); //获取开始时间 int a = f(20); System.out.println(a); long endTime = System.nanoTime(); //获取结束时间 System.out.println("time:" + (endTime - startTime) + "ns"); //输出程序运行时间 } private static Integer f(int n){ if (n==0)return 0; int[] b = new int[n+1]; return save(b,n); } private static Integer save(int[] a,int n){ if (n ==1||n==2)return 1; if (a[n]!=0)return a[n]; a[n] = save(a, n-1)+save(a,n-2); return a[n]; } }
可以看到,速度整整快了三倍多,这只是简单的一个比较,我们再来算一下时间复杂度。
A:
因为我们将每一次计算的结果都保存在数组中,所以不存在重复的计算,输入的值为N时,所要解决的问题也就是N个,每个问题所需的时间为O(1),总的时间复杂度也就是O(N)。相比纯递归根本不是一个级别的差异。