活动地址：CSDN21天学习挑战赛

前言

例如：今天来介绍一下一道经典的算法题——水仙花数，第一次发博客，写得不好，还请多多包涵。

提示：以下是本篇文章正文内容，下面案例可供参考

一、水仙花数

问题来源：

https://www.nowcoder.com/practice/dc943274e8254a9eb074298fb2084703?tpId=290&tqId=105636&ru=/exam/oj/ta&qru=/ta/beginner-programmers/question-ranking&sourceUrl=%2Fexam%2Foj%2Fta%3Fpage%3D1%26tpId%3D290%26type%3D290

描述

春天是鲜花的季节，水仙花就是其中最迷人的代表，数学上有个水仙花数，他是这样定义的： “水仙花数”是指一个三位数，它的各位数字的立方和等于其本身，比如：153=1^3+5^3+3^3。 现在要求输出所有在m和n范围内的水仙花数。

输入描述：

输入数据有多组，每组占一行，包括两个整数m和n（100 ≤ m ≤ n ≤ 999）。

输出描述：

对于每个测试实例，要求输出所有在给定范围内的水仙花数，就是说，输出的水仙花数必须大于等于m,并且小于等于n，如果有多个，则要求从小到大排列在一行内输出，之间用一个空格隔开; 如果给定的范围内不存在水仙花数，则输出no; 每个测试实例的输出占一行。

分析问题：

我们要把一个三位数的每一位数都单独拆出来，然后三次方运算后加起来得到原来的数。那题目的关键就在与怎么把三个数分别拆出来。

核心步骤（拆数）：

我们学过的运算法则里面，用来拆数的，最基础的步骤就是运用除法，还有求余数了。

例如：100/10=10   ；  600/10=60 ；对于刚好可以整除的数来说，不难理解，除以十就是小数点往左移动一位，除以百，千也是以此类推，和初中数学一样了。

但是对于不能整除的数呢？

例如：512/10 ；要是按我们以前学过的数学，512/10=51.2 ；但是在这里，小数点会自己舍去。也就是说512/10=51。

小结：对于整数/10，小数点就是往左移动一位，去除了最右边的那一位数。

求余数呢，推理过程大多相同，这里直接上结论了。

结论：一个整数%10=（保留最右边的那一位数字），是不是发现求余和除法的保留数字刚好反了过来。

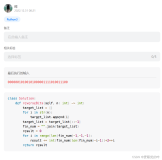
具体代码如下:

#include <stdio.h>
int main() {
    int m, n;
    while (scanf("%d %d", &m, &n) != EOF) {   //多组输入一个区间
        int flag = 0;
        for (int i = m; i <= n; i++) {  //这个区间里的每一个数都算一遍；下面把i假设为512具体解释
            int g = i % 10;     // 512%10=2 保留最右边一位
            int s = i / 10 % 10;  // 512/10=51（去掉最右一位）51%10=1（相当于保留原来的第二位）
            int b = i / 100;  // 512/100=5（保留最左一位）
            if (i == g * g * g + s * s * s + b * b * b) {  //这样每一位数都拆出来了
                printf("%d ", i);
                flag = 1;
            }
        }
        if (flag == 0)
            printf("no\n");
        else
            printf("\n");
    }
    return 0;
}

总结

以上就是今天要讲的内容，本文仅仅简单介绍了解水仙花数的核心手法，拆数，希望对大家有帮助~