
现在Codancer有两个长度均为n的数组a数组和b数组,其中对于a中的 每 个 元 素 a[i] 都 有 (-10^6<=a[i]<=10^6), 对 于 b 中 的 每 个 元 素 b[i] 都 有(0<=b[i]<=n),对于每个 i(1<=i<=n),我们定义区间 [L,R] 是合法的只有 [L,R] 满足下面的条件: 1. 1<=L<=R<=n 2. 0<=i-L,R-i<=b[i] 现在对于每个 i,Codancer 想找到一组合法区间使得 (a[L]+a[L+1]+...a[R]) 最大,并将这个最大值记为 s[i]。现在请计算 (s[1]+s[2]+s[3]+...+s[n])。输入包含一个 n(1<=n<=10^5) 和两个数组 b,a。(b 在前面,a 在后面 )输出 s 数组的和。
版权声明:本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单进行举报,一经查实,本社区将立刻删除涉嫌侵权内容。
S[1]=a[1]+a[2]=-4,此时 S[1] 最大 S[2]=a[2]+a[3]+a[4]=6, 此时 S[2] 最大 同理可得 S[3]=a[2]+a[3]+a[4]=6, S[4]=a[2]+a[3]+a[4], S[5]=a[2]+a[3]+a[4]+a[5]=2 因此答案为 S[1]+S[2]+S[3]+S[4]+S[5]=16。 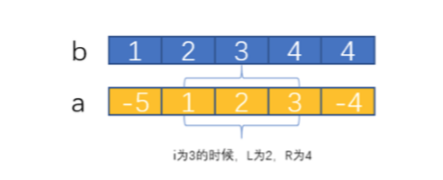
考虑对 a 数组做前缀和数组 pre, 即 pre[i] 是 (a[1]+a[2]+...+a[i]) 的值,同时对a 做后缀和数组 sa, 即 sa[i] 是 (a[i]+a[i+1]+...a[n]) 的值,那么 s[i] 可以由两部分组成,左边的 a[L]+...+a[i],右边的 a[i]+...+a[R]。左边其实就是找到一个 L,使得 a[L]+...+a[i] 尽可能的大,右边同理 , 因此左边其实就是 max(sa[max(1,i-k)]...sa[i])-sa[i+1]。右边是 max(pre[i]...pre[min(i+k,n)])。对前缀和和后缀和分别建立线段树,O(log(n))求解s[i]即可,答案会爆int,因此需要用 long long 存储。 因此输入:5 [1,2,3,4,4] [-5,1,2,3,-4] 输出:16 注意 : s[1]=-4 s[2]=6 s[3]=6 s[4]=6 s[5]=2 因此最终答案为 16