
先看下题目,LeetCode 第 986 题就是这个问题:
给定两个由一些闭区间组成的列表,每个区间列表都是成对不相交的,并且已经排序。
返回这两个区间列表的交集。
(形式上,闭区间 [a, b](其中 a <= b)表示实数 x 的集合,而 a <= x <= b。两个闭区间的交集是一组实数,要么为空集,要么为闭区间。例如,[1, 3] 和 [2, 4] 的交集为 [2, 3]。)
示例:
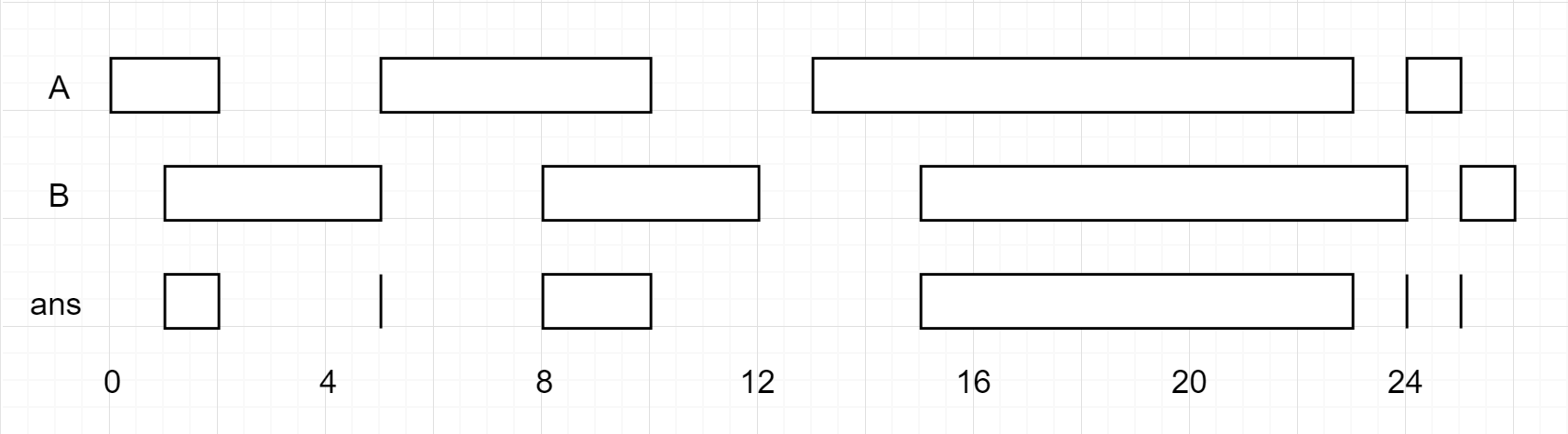
输入:A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
输出:[[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
注意:输入和所需的输出都是区间对象组成的列表,而不是数组或列表。
题目很好理解,就是让你找交集,注意区间都是闭区间。
思路分析
解决区间问题的思路一般是先排序,以便操作,不过题目说已经排好序了,那么可以用两个索引指针在 A 和 B 中游走,把交集找出来,代码大概是这样的:
# A, B 形如 [[0,2],[5,10]...]
def intervalIntersection(A, B):
i, j = 0, 0
res = []
while i < len(A) and j < len(B):
# ...
j += 1
i += 1
return res
不难,我们先老老实实分析一下各种情况。
首先,对于两个区间,我们用 [a1,a2] 和 [b1,b2] 表示在 A 和 B 中的两个区间,那么什么情况下这两个区间没有交集呢:
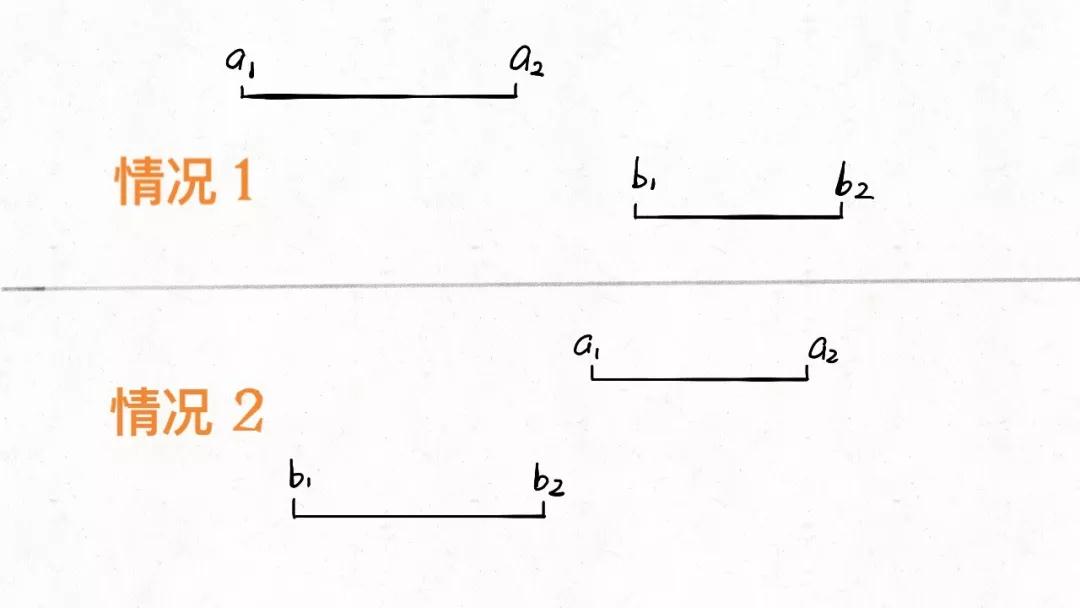
只有这两种情况,写成代码的条件判断就是这样:
if b2 < a1 or a2 < b1:
[a1,a2] 和 [b1,b2] 无交集
那么,什么情况下,两个区间存在交集呢?根据命题的否定,上面逻辑的否命题就是存在交集的条件:
# 不等号取反,or 也要变成 and
if b2 >= a1 and a2 >= b1:
[a1,a2] 和 [b1,b2] 存在交集
接下来,两个区间存在交集的情况有哪些呢?穷举出来:
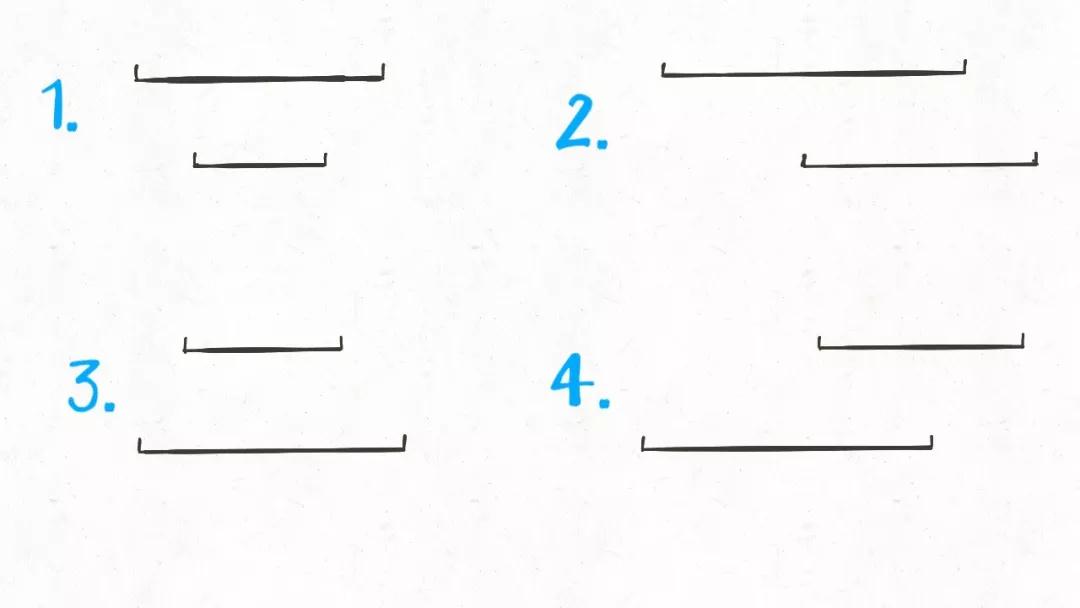
这很简单吧,就这四种情况而已。那么接下来思考,这几种情况下,交集是否有什么共同点呢?
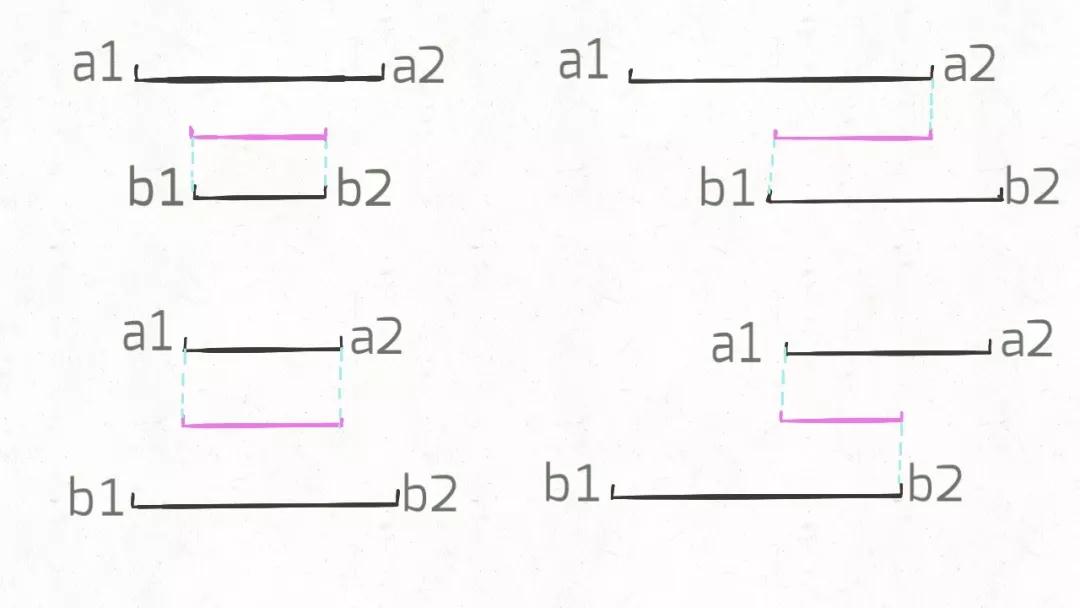
我们惊奇地发现,交集区间是有规律的!如果交集区间是[c1,c2],那么c1=max(a1,b1),c2=min(a2,b2)!这一点就是寻找交集的核心,我们把代码更进一步:
while i < len(A) and j < len(B):
a1, a2 = A[i][0], A[i][1]
b1, b2 = B[j][0], B[j][1]
if b2 >= a1 and a2 >= b1:
res.append([max(a1, b1), min(a2, b2)])
# ...
最后一步,我们的指针i和j肯定要前进(递增)的,什么时候应该前进呢?
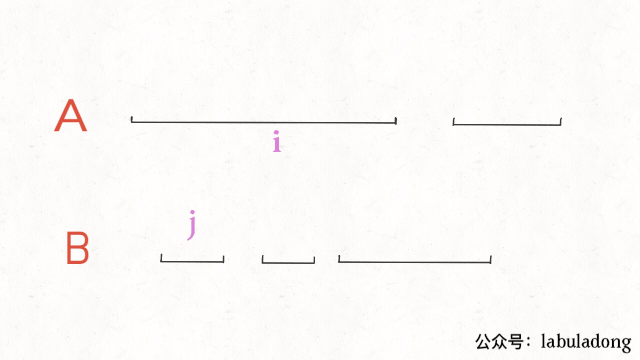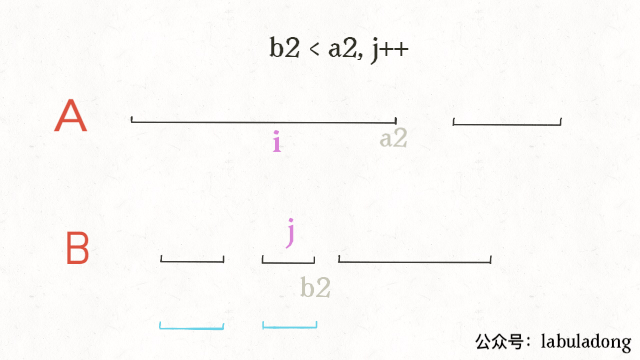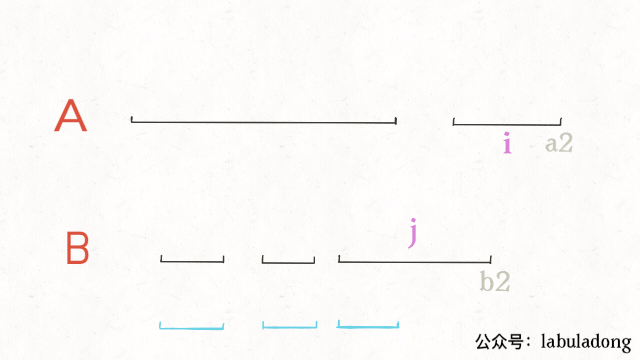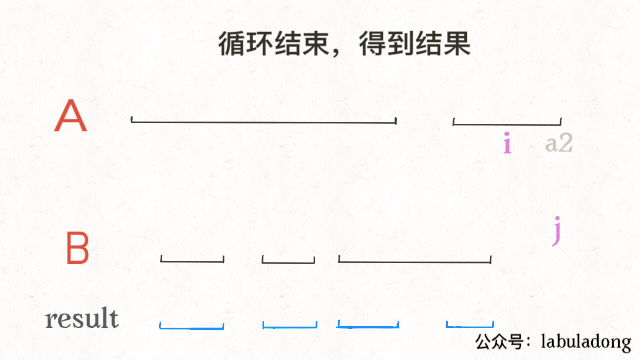
结合动画示例就很好理解了,是否前进,只取决于a2和b2的大小关系:
while i < len(A) and j < len(B):
# ...
if b2 < a2:
j += 1
else:
i += 1
代码实现
# A, B 形如 [[0,2],[5,10]...]
def intervalIntersection(A, B):
i, j = 0, 0 # 双指针
res = []
while i < len(A) and j < len(B):
a1, a2 = A[i][0], A[i][1]
b1, b2 = B[j][0], B[j][1]
# 两个区间存在交集
if b2 >= a1 and a2 >= b1:
# 计算出交集,加入 res
res.append([max(a1, b1), min(a2, b2)])
# 指针前进
if b2 < a2: j += 1
else: i += 1
return res
总结一下,区间类问题看起来都比较复杂,情况很多难以处理,但实际上通过观察各种不同情况之间的共性可以发现规律,用简洁的代码就能处理。
另外,区间问题没啥特别厉害的奇技淫巧,其操作也朴实无华,但其应用却十分广泛。
来源 | github
作者 | labuladong
版权声明:本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单进行举报,一经查实,本社区将立刻删除涉嫌侵权内容。