【今日算法】4月28日-区间调度问题之区间合并

对于区间相关的问题，有很多类型，本文就来讲讲区间合并问题（Merge Interval）。

LeetCode 第 56 题就是一道相关问题，题目很好理解：

给出一个区间的集合，请合并所有重叠的区间。

示例 1:

输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2:

输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。

我们解决区间问题的一般思路是先排序，然后观察规律。

一、思路

一个区间可以表示为 [start, end]，前文聊的区间调度问题，需要按 end 排序，以便满足贪心选择性质。而对于区间合并问题，其实按 end 和 start 排序都可以，不过为了清晰起见，我们选择按 start 排序。

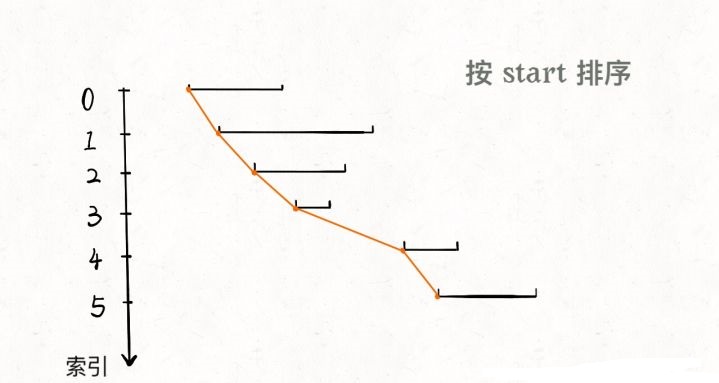
显然，对于几个相交区间合并后的结果区间 x，x.start 一定是这些相交区间中 start 最小的，x.end 一定是这些相交区间中 end 最大的。

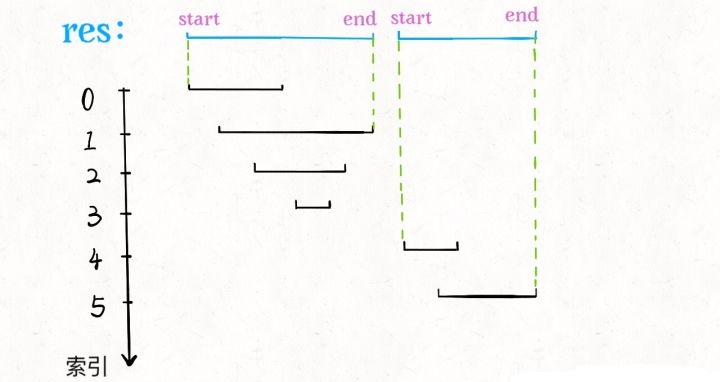
由于已经排了序，x.start 很好确定，求 x.end 也很容易，可以类比在数组中找最大值的过程：

int max_ele = arr[0];
for (int i = 1; i < arr.length; i++) 
    max_ele = max(max_ele, arr[i]);
return max_ele;

二、代码

# intervals 形如 [[1,3],[2,6]...]
def merge(intervals):
    if not intervals: return []
    # 按区间的 start 升序排列
    intervals.sort(key=lambda intv: intv[0])
    res = []
    res.append(intervals[0])

    for i in range(1, len(intervals)):
        curr = intervals[i]
        # res 中最后一个元素的引用
        last = res[-1]
        if curr[0] <= last[1]:
            # 找到最大的 end
            last[1] = max(last[1], curr[1])
        else:
            # 处理下一个待合并区间
            res.append(curr)
    return res

看下动画就一目了然了：

至此，区间合并问题就解决了。

来源 | github

作者 | labuladong